X
Код презентации скопируйте его
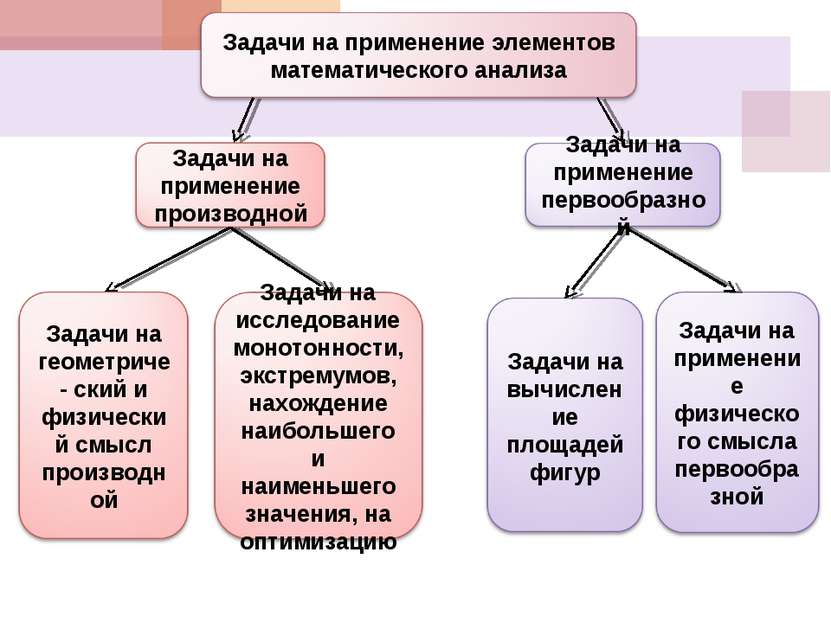
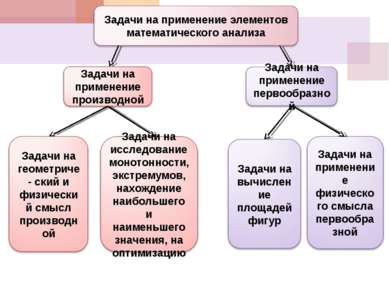
Применение элементов математического анализа при решении задач
Скачать эту презентацию
Презентация на тему Применение элементов математического анализа при решении задач
Скачать эту презентациюCлайд 1
Применение элементов математического анализа при решении задач (по материалам ЕГЭ – 2010-2011)
Cлайд 2
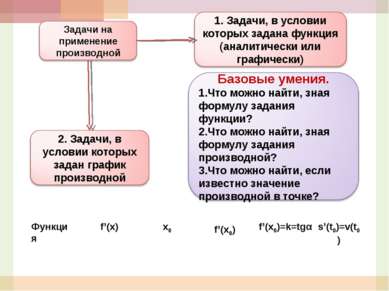
- Учиться проводить анализ условия задачи, что помогает поиску способа решения; Цели урока - Учиться переводить язык задачи на язык производной или первообразной; - Учиться выстраивать цепочку логических рассуждений при переходе от языка функции к языку геометрии или механики
Cлайд 3
Cлайд 4
Функция f’(x) x0 f’(x0) f’(x0)=k=tgα s’(t0)=v(t0)
Cлайд 5
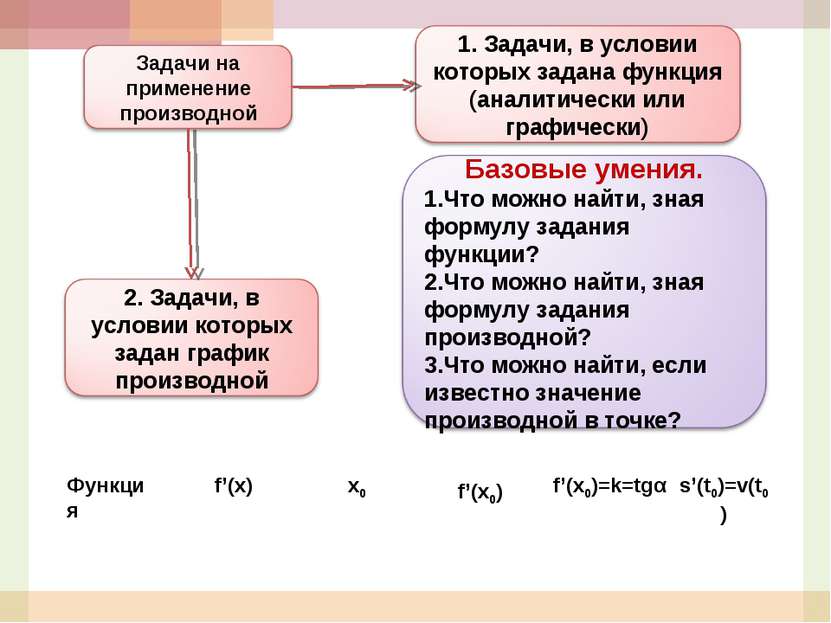
? 1б) Составьте задачу с другими числовыми данными, которая решается по плану: f’(x), f’(x0), k= f’(x0). 1а)Выполните анализ условия задачи и наметьте план её решения: Найдите тангенс угла наклона касательной, проведенной к графику функции f(x) =5x2+7x+2 в точке с абсциссой х0 =2. Функция f’(x) x0 f’(x0) f’(x0)=k=tgα s’(t0)=v(t0) f(x)=5x2+7x+2 2 1 3 2 1в) Сформулируйте задачу, обратную 1а) и составьте план её решения. Найдите абсциссу точки касания, если тангенс угла наклона касательной к графику функции f(x) =5x2+7x+2 равен 27 Функция f’(x) x0 f’(x0) f’(x0)=k=tgα f(x)=5x2+7x+2 1 3 2 27 f’(x0) =27 Найдите угловой коэффициент касательной к графику первообразной функции F(x) функции f(x) = … в точке абсциссой … Что известно по условию задачи? Как задана функция? Что еще известно? Что нужно найти? Как находят тангенс угла наклона касательной, проведенной к графику заданной функции в заданной точке?
Cлайд 6
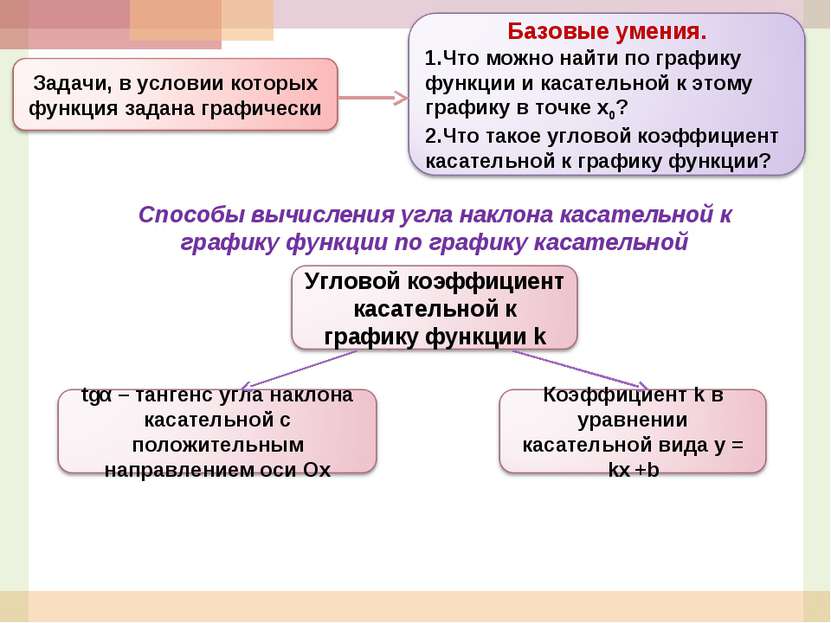
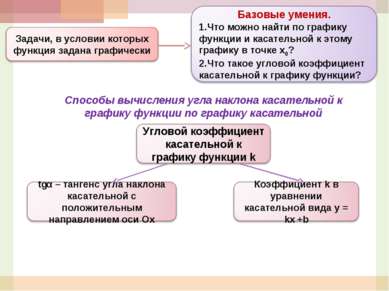
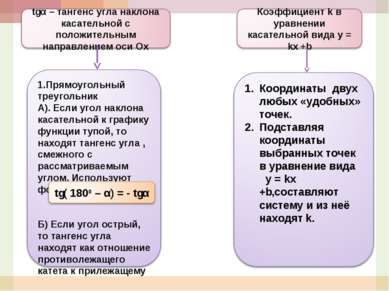
Прочитайте задачу: В точке А графика функции у = 5x3+4x+1 проведена касательная к нему, параллельная прямой у = 4х + 3. Найдите сумму координат точки А. Обоснуйте следующий план решения задачи: к =4; f’(x); f’(x0) = 4; х0 из уравнения; ответ на вопрос задачи. Ответьте на вопросы анализа условия задачи на физический смысл производной: точка движется по координатной прямой по закону s(t) = t3/3 – 2t2+3t -15 (s- расстояние в см, t – время в секундах, прошедшее с момента движения). Определите скорость и ускорение точки через 3 с после начала движения. Закон движения S(t) t0 V(t0) = S’(t0) a(t0) = v’ (t0) Что известно из условия задачи? Как задана функция? Что ещё известно? Что нужно найти? Что известно по условию задачи?(функция) Как задана функция?(формулой) Что еще известно?(х0) Что нужно найти?( к, tgα) Как находят тангенс угла наклона касательной, проведенной к графику заданной функции в заданной точке?
Cлайд 7
Способы вычисления угла наклона касательной к графику функции по графику касательной
Cлайд 8
Cлайд 9
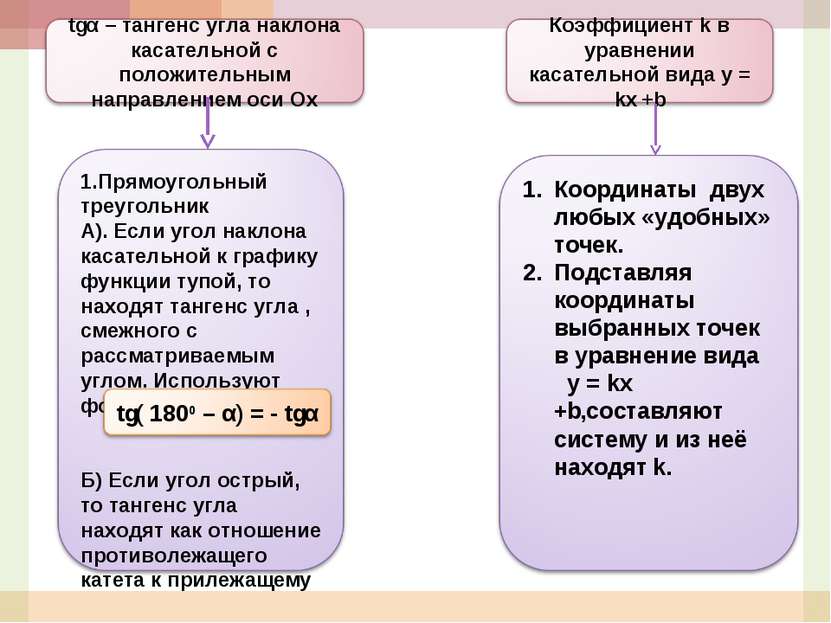
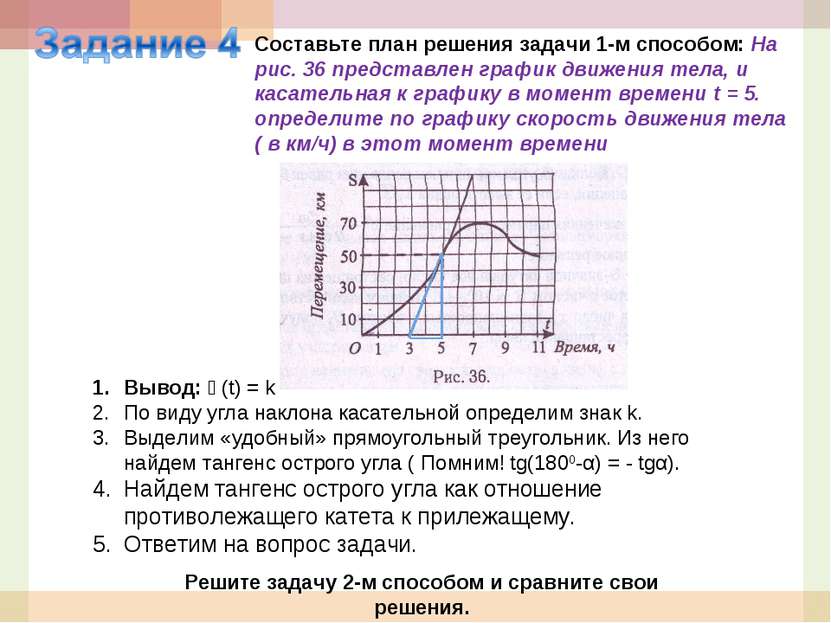
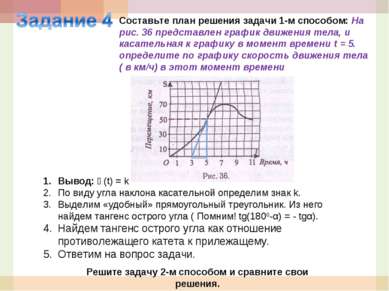Составьте план решения задачи 1-м способом: На рис. 36 представлен график движения тела, и касательная к графику в момент времени t = 5. определите по графику скорость движения тела ( в км/ч) в этот момент времени Решите задачу 2-м способом и сравните свои решения. Вывод: ϑ(t) = k По виду угла наклона касательной определим знак k. Выделим «удобный» прямоугольный треугольник. Из него найдем тангенс острого угла ( Помним! tg(1800-α) = - tgα). Найдем тангенс острого угла как отношение противолежащего катета к прилежащему. Ответим на вопрос задачи.
Cлайд 10
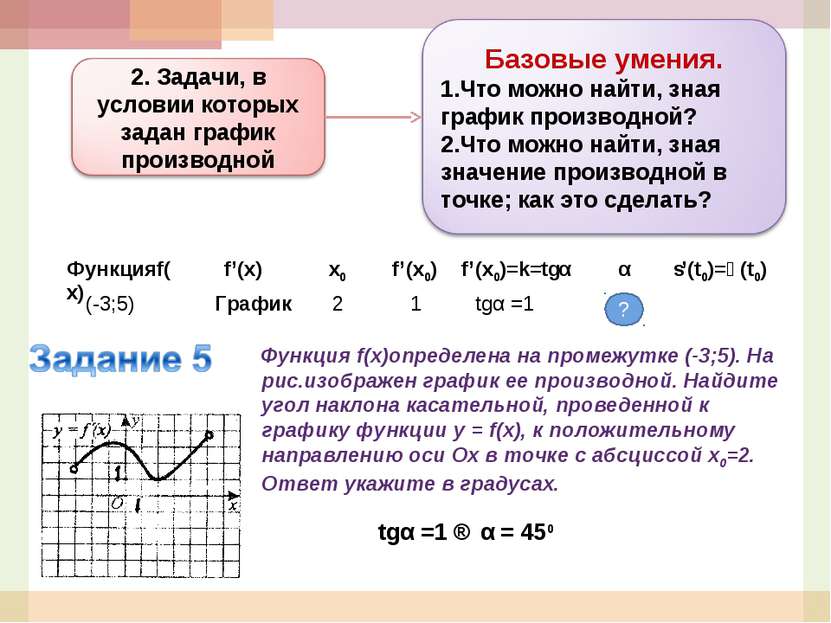
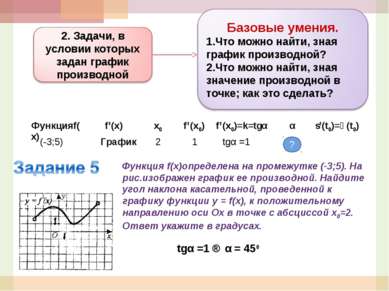Функция f(x)определена на промежутке (-3;5). На рис.изображен график ее производной. Найдите угол наклона касательной, проведенной к графику функции y = f(x), к положительному направлению оси Ох в точке с абсциссой х0=2. Ответ укажите в градусах. (-3;5) График 2 tgα =1 tgα =1 ⇒ α = 450 ? 1 Функцияf(x) f’(x) x0 f’(x0) f’(x0)=k=tgα α s’(t0)=ϑ(t0)
Cлайд 11
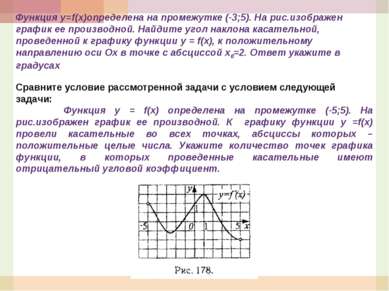Функция у=f(x)определена на промежутке (-3;5). На рис.изображен график ее производной. Найдите угол наклона касательной, проведенной к графику функции y = f(x), к положительному направлению оси Ох в точке с абсциссой х0=2. Ответ укажите в градусах Сравните условие рассмотренной задачи с условием следующей задачи: Функция у = f(x) определена на промежутке (-5;5). На рис.изображен график ее производной. К графику функции у =f(x) провели касательные во всех точках, абсциссы которых –положительные целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.
Cлайд 12
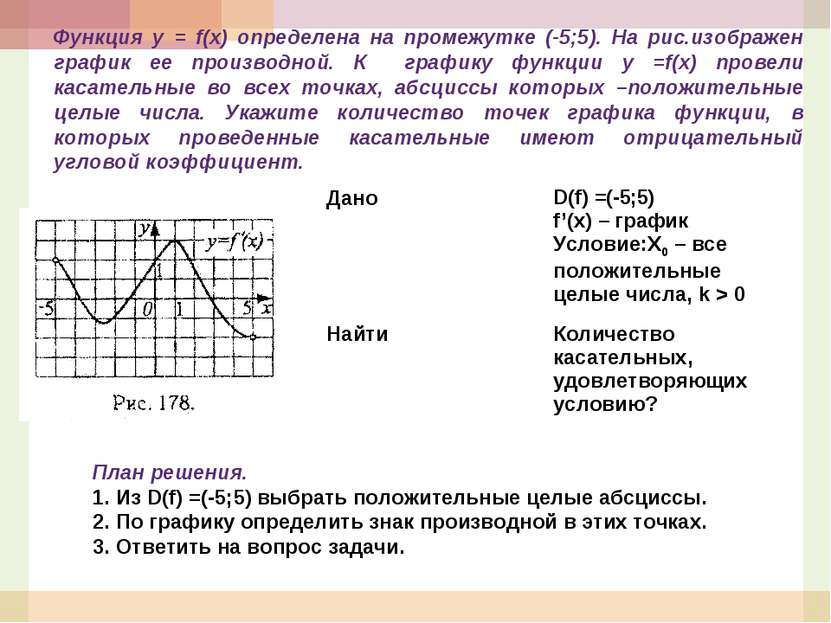
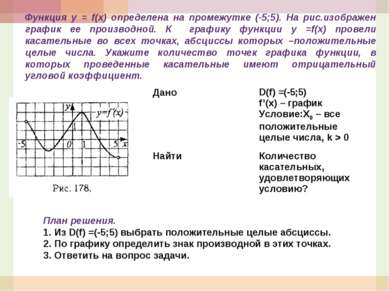Функция у = f(x) определена на промежутке (-5;5). На рис.изображен график ее производной. К графику функции у =f(x) провели касательные во всех точках, абсциссы которых –положительные целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент. План решения. 1. Из D(f) =(-5;5) выбрать положительные целые абсциссы. 2. По графику определить знак производной в этих точках. 3. Ответить на вопрос задачи. Дано D(f) =(-5;5) f’(x) – график Условие:Х0 – все положительные целые числа, k > 0 Найти Количество касательных, удовлетворяющих условию?
Cлайд 13
Функция у = f(x) определена на промежутке (-3;5). На рис.изображен график ее производной. Укажите количество точек графика функции, в которых касательные наклонены под углом 1500 к положительному направлению оси абсцисс. α =1500, tg α < 0, k
Cлайд 14
Использованная литература Материалы курсов повышения квалификации при Брянском государственном университете имени академика И.Г.Петровского
