X
Код презентации скопируйте его
Применение производной к исследованию функций
Скачать эту презентацию
Презентация на тему Применение производной к исследованию функций
Скачать эту презентациюCлайд 1
Тема: «Применение производной к исследованию функции» МБОУ Кавалерская средняя общеобразовательная школа №3 имени Героя Советского Союза А.П. Дубинца Учитель Стрельцова Светлана Владимировна
Cлайд 2
Цель урока – закрепить и систематизировать знания учащихся по исследованию функций с помощью производной.
Cлайд 3
Применение производной к исследованию функции 1) промежутки возрастания, убывания 3) наибольшее и наименьшее значение функции 2) точки экстремума и значение функции в этих точках 4) построение графика функции
Cлайд 4
Вопросы 1) Какая функция называется возрастающей? 2) Какая функция называется убывающей? 3) Как связан “знак” производной с возрастанием и убыванием функции ? 4) Что называется точкой максимума? 5) Что называется точкой минимума? 6) Какие точки называются стационарными? 7) Какие точки называются критическими? 8) Каков алгоритм нахождения наибольшего и наименьшего значений непрерывной на заданном отрезке функции?
Cлайд 5
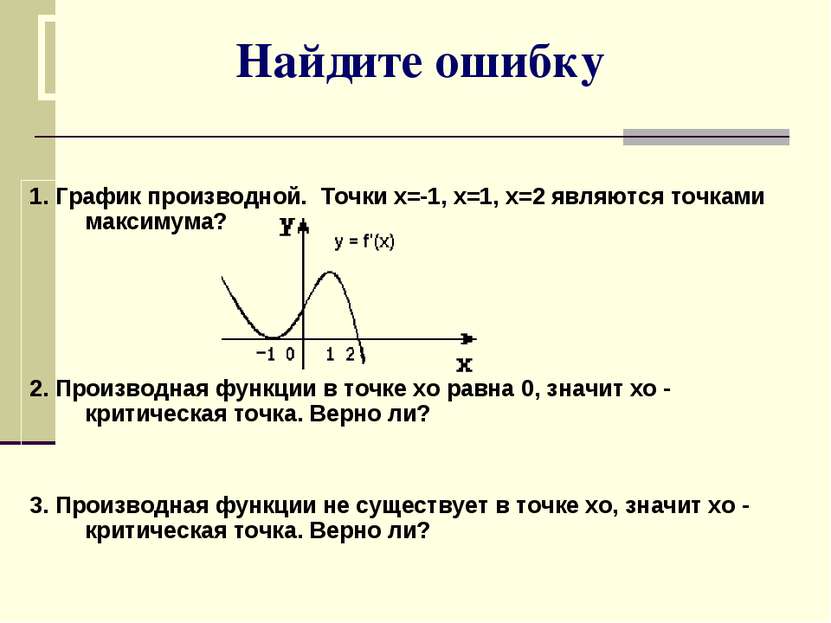
Найдите ошибку 1. График производной. Точки х=-1, х=1, х=2 являются точками максимума? 2. Производная функции в точке хо равна 0, значит хо - критическая точка. Верно ли? 3. Производная функции не существует в точке хо, значит хо - критическая точка. Верно ли?
Cлайд 6
4. Критическая точка является точкой экстремума. Верно ли? 5. Точка экстремума является критической точкой. Верно ли? 6. Функция y(x) непрерывна в точке x=4, причем y' (x)>0 на (1;4) и y'(x)
Cлайд 7
«Математическая перестрелка»
Cлайд 8
«Бег с препятствиями»
Cлайд 9
Из истории Он ввёл термин «производная» в 1797 г., что является буквальным переводом на русский язык французского слова deviree, он же ввел современные обозначения y , f . Такое название отражает смысл понятия: функция f (х) происходит из f(х), является производной от f(х). Один из создателей (вместе с И. Ньютоном) дифференциального и интегрального исчислений В 1675 г показал взаимно-обратный характер дифференцирования и интегрирования. По просьбе Петра I разработал проекты развития образования и государственного управления в России.
Cлайд 10
Задание: Найти экстремумы функции. 1) y = x3 + 6x2 - 15x - 3 2) y = 2х - x² y = x3 - 6x2 - 15x + 7 3) y = x/4 + 9/x 4) y = x/4 + 4/x 5) y = x – х4/4 (y = 8x – х4/4) 6) y = x3 - 6x2 - 15x + 7 7) у = х³-6х²
Cлайд 11
Жозеф Луи Лагранж (1736-1813) французский математик и механик, иностранный почетный член Петербургской АН (1776). Готфрид Вильгельм Лейбниц (1646-1716), немецкий философ, математик, физик, языковед.
Cлайд 12
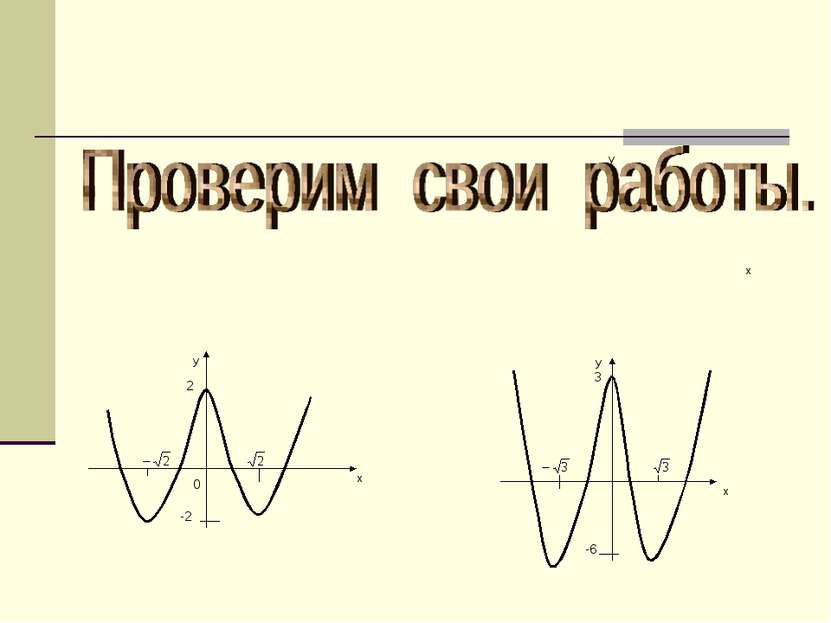
З а д а н и я Для функции у = f(х) найдите: 1) область определения; 2) производную; 3) критические точки; 4) Промежутки монотонности и экстремумы. По результатам исследования постройте график. 0 3 4 2 4 2 Вариант Функция у = f(х) 1 f(х)= х -4х +2 2 f(х)=х - 6х +3
Cлайд 13
х х х у у у 2 -2 0 3 -6
Cлайд 14
Пословицы и графики функций Первая женщина математик С. В. Ковалевская сказала: « Математик должен быть поэтом в душе». Подберите к графикам функций, изображенных на слайдах, пословицы, которые раскрывают суть процессов функции
Cлайд 15
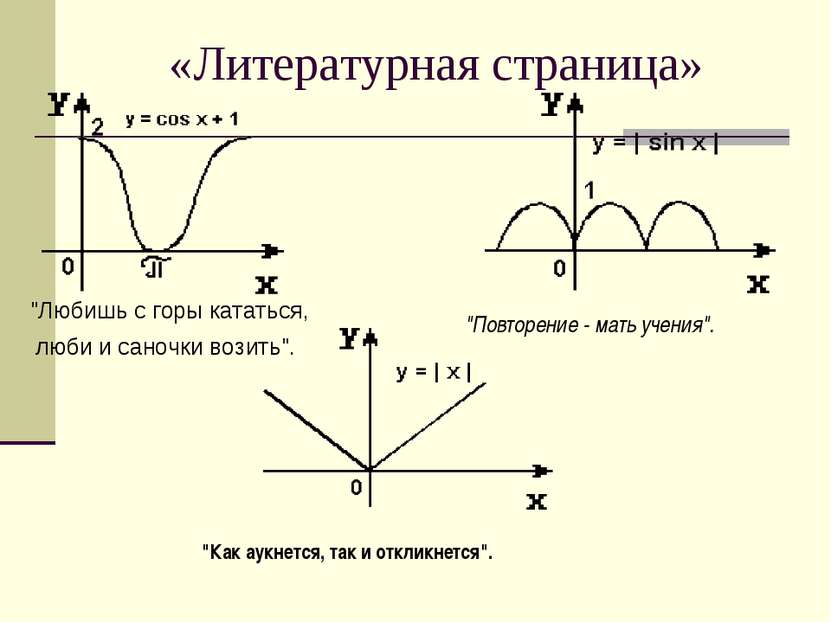
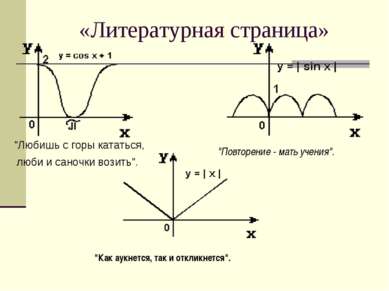«Литературная страница» "Любишь с горы кататься, люби и саночки возить". "Повторение - мать учения". "Как аукнется, так и откликнется".
Cлайд 16
Итог урока Продолжите фразу: Сегодня на уроке я повторил… Сегодня на уроке я закрепил… Мне предстоит повторить…
Cлайд 17
Домашнее задание Работа по карточкам 2 варианта
Cлайд 18
С П А С И Б О !!! До свидания!
