X
Код презентации скопируйте его
Собирающие линзы
Скачать эту презентацию
Презентация на тему Собирающие линзы
Скачать эту презентациюCлайд 1
Cлайд 2
линзы, преобразующие параллельный пучок световых лучей в сходящийся: двояковыпуклые плоско-выпуклые выпукло-вогнутые
Cлайд 3
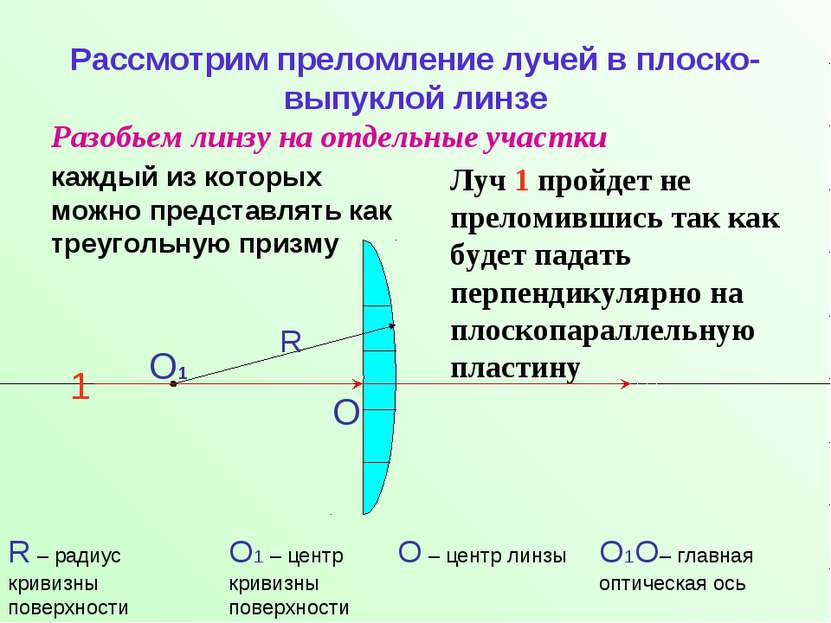
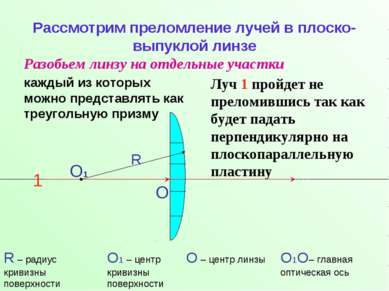Рассмотрим преломление лучей в плоско-выпуклой линзе Разобьем линзу на отдельные участки каждый из которых можно представлять как треугольную призму R – радиус кривизны поверхности О R Луч 1 пройдет не преломившись так как будет падать перпендикулярно на плоскопараллельную пластину 1 О1 О – центр линзы О1 – центр кривизны поверхности О1О– главная оптическая ось
Cлайд 4
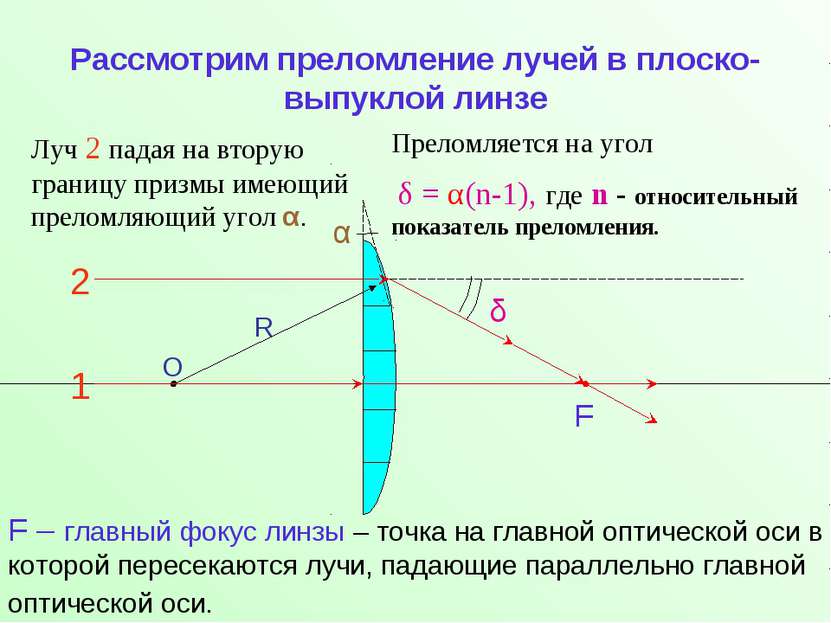
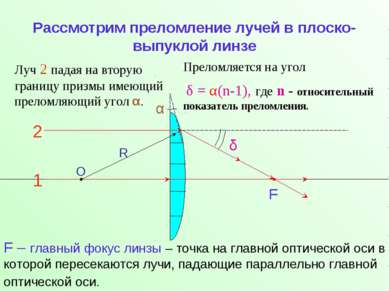Рассмотрим преломление лучей в плоско-выпуклой линзе О R 2 1 Луч 2 падая на вторую границу призмы имеющий преломляющий угол α. α F Преломляется на угол δ = α(n-1), где n - относительный показатель преломления. δ F – главный фокус линзы – точка на главной оптической оси в которой пересекаются лучи, падающие параллельно главной оптической оси.
Cлайд 5
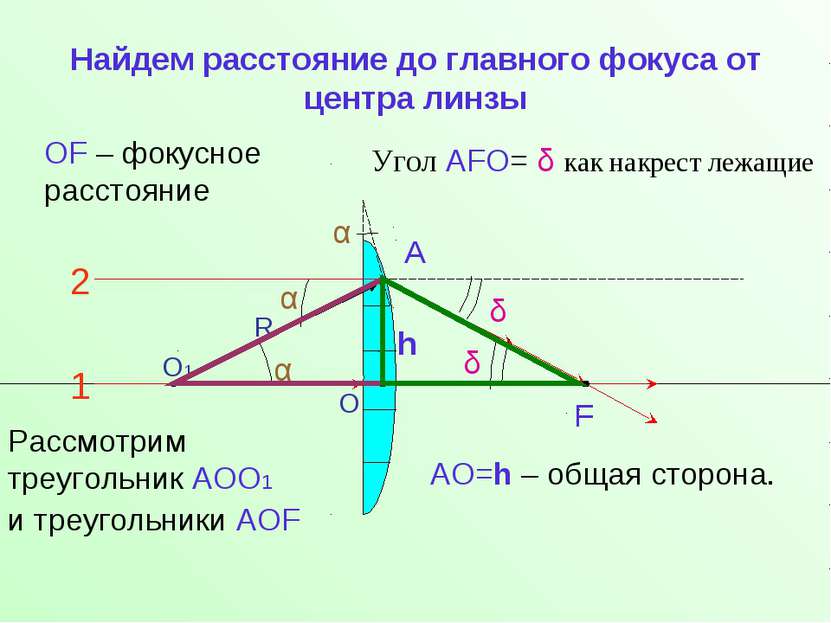
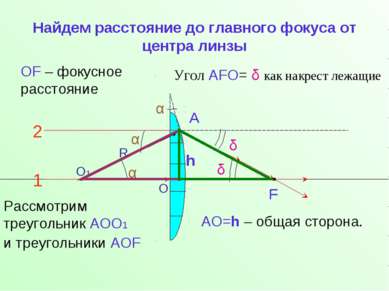Найдем расстояние до главного фокуса от центра линзы О1 R 2 1 α F δ О ОF – фокусное расстояние α α δ Угол АFО= δ как накрест лежащие А h Рассмотрим треугольник АОО1 и треугольники АОF АО=h – общая сторона.
Cлайд 6
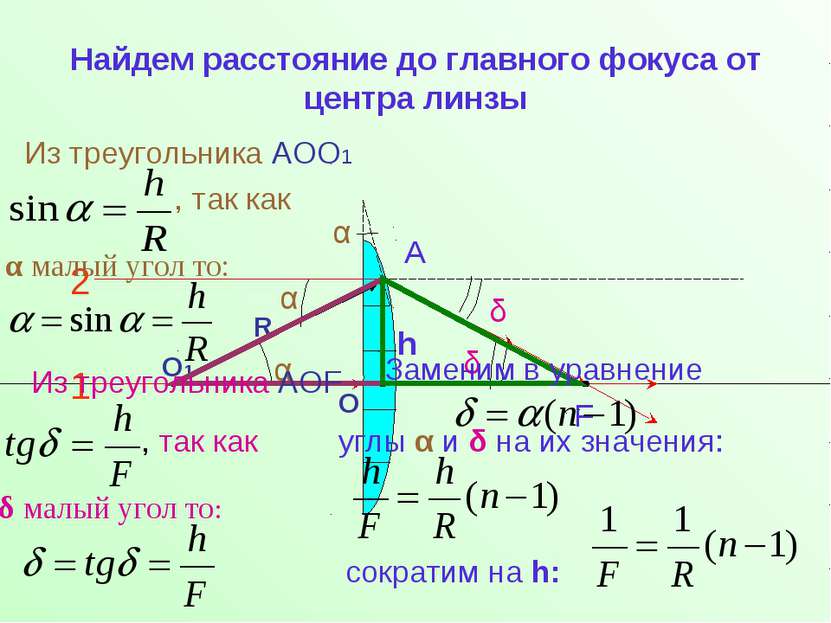
Найдем расстояние до главного фокуса от центра линзы Из треугольника АОО1 , так как α малый угол то: Из треугольника АOF , так как δ малый угол то: Заменим в уравнение углы α и δ на их значения: сократим на h:
Cлайд 7
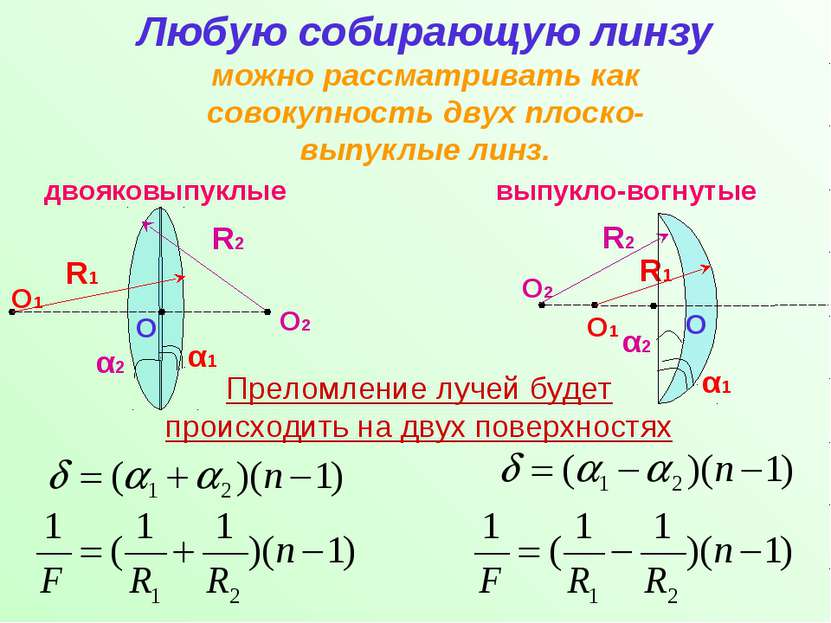
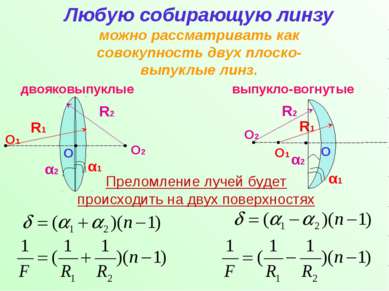двояковыпуклые выпукло-вогнутые Любую собирающую линзу можно рассматривать как совокупность двух плоско-выпуклые линз. O2 Преломление лучей будет происходить на двух поверхностях
Cлайд 8
Оптическая сила линзы - физическая величина, обратная фокусному расстоянию. Диоптрия - оптическая сила линзы с фокусным расстоянием 1 метр
Cлайд 9
Для собирающих линз двояковыпуклые плоско-выпуклые выпукло-вогнутые ,так как R1>0 R2>0 ,так как R>0 ,так как |R2|>R1
Cлайд 10
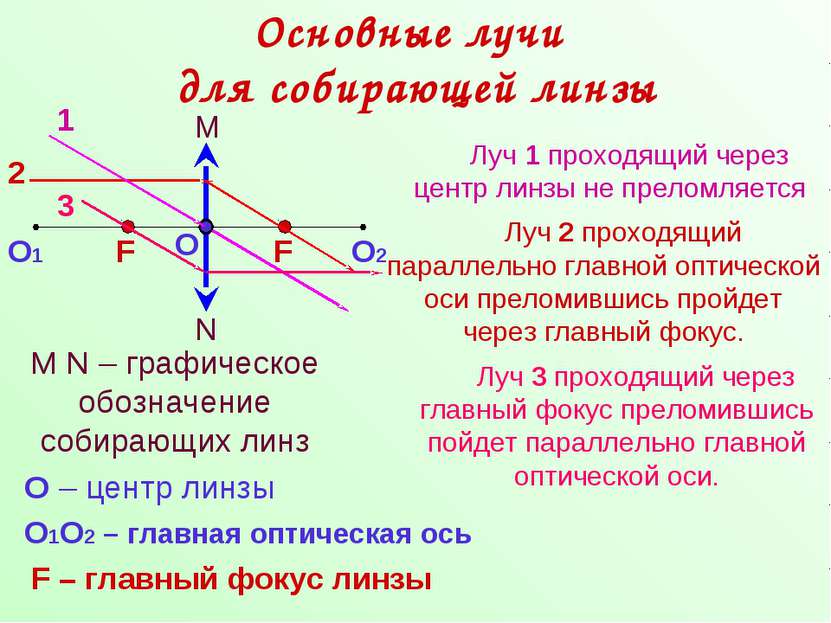
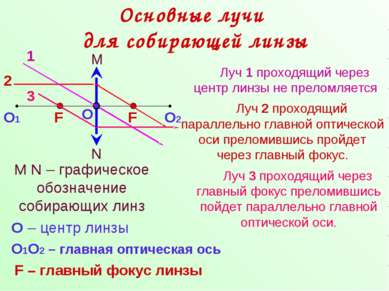Основные лучи для собирающей линзы N M M N – графическое обозначение собирающих линз О О – центр линзы О1 О2 О1О2 – главная оптическая ось F F F – главный фокус линзы Луч 1 проходящий через центр линзы не преломляется 1 Луч 2 проходящий параллельно главной оптической оси преломившись пройдет через главный фокус. 2 Луч 3 проходящий через главный фокус преломившись пойдет параллельно главной оптической оси. 3
Cлайд 11
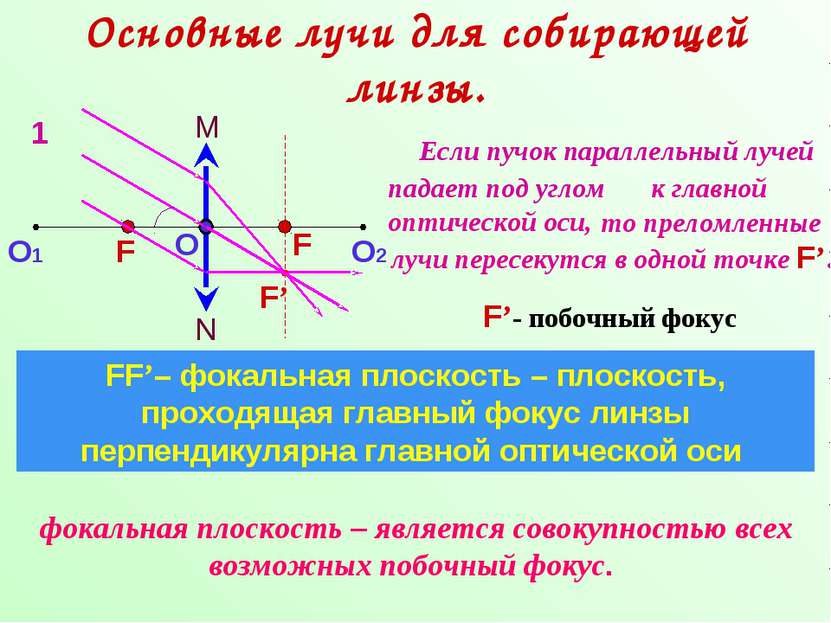
Основные лучи для собирающей линзы. N M О О1 О2 F F FF’– фокальная плоскость – плоскость, проходящая главный фокус линзы перпендикулярна главной оптической оси Если пучок параллельный лучей падает под углом γ к главной оптической оси, то преломленные лучи пересекутся в одной точке F’. γ F’ F’- побочный фокус 1 фокальная плоскость – является совокупностью всех возможных побочный фокус.
Cлайд 12
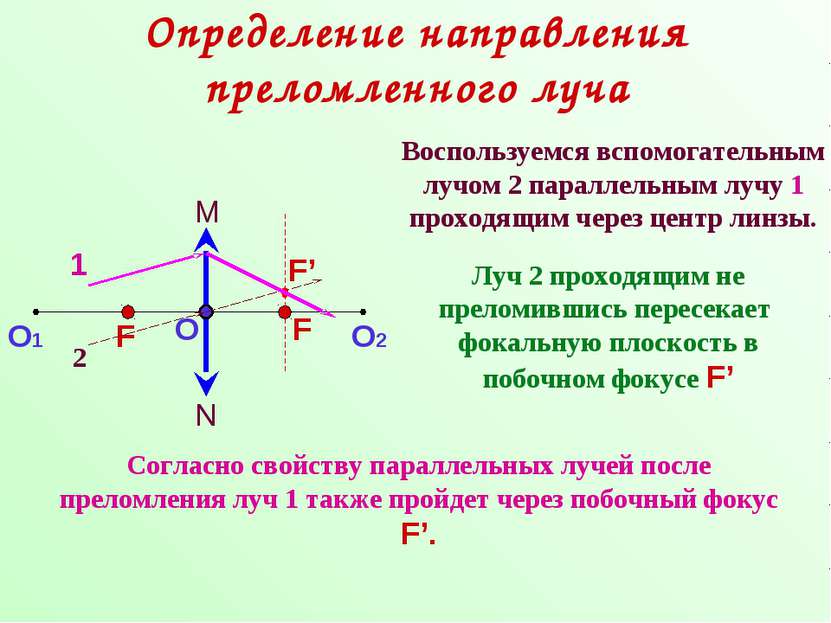
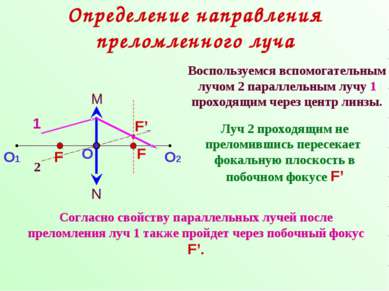Определение направления преломленного луча Воспользуемся вспомогательным лучом 2 параллельным лучу 1 проходящим через центр линзы. 1 2 Луч 2 проходящим не преломившись пересекает фокальную плоскость в побочном фокусе F’ F’ Согласно свойству параллельных лучей после преломления луч 1 также пройдет через побочный фокус F’.
Cлайд 13
Определение направления падающего луча 3 2 Луч 3 проходящим не преломившись пересекает фокальную плоскость в побочном фокусе F’ F’ Согласно свойству параллельных лучей после преломления луч 2 также пройдет через побочный фокус F’ По принципу обратимости лучей, будем считать, что луч 2 падающий луч. Воспользуемся вспомогательным лучом 3 параллельным лучу 2 проходящим через центр линзы.
Cлайд 14
2. Выяснили связь между геометрическими размерами линзы и ее физическими свойствами собирающей линзы 1. Рассмотрели ход лучей в собирающих линзах; 3. Обнаружили cвязь между основными физическими величинами характеризующими собирающей линзу Вывод презентации 4. выяснили основные свойства замечательных лучей в собирающей линзу
