X
Код презентации скопируйте его
ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Скачать эту презентацию
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Скачать эту презентациюCлайд 1
Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназия №1 г.Лебедянь Липецкой области
Cлайд 2
Укажите номера верных утверждений * 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если угол равен 25⁰, то смежный с ним угол равен 155⁰ 3.Через любую точку плоскости можно провести не менее одной прямой
Cлайд 3
* Сформулируйте аксиому о взаимном расположении прямой и точек. Каким свойством обладают смежные углы? Сколько прямых можно провести через точку на плоскости? Через любые две точки проходит прямая , и притом только одна Сумма смежных углов равна 180° Через точку на плоскости можно провести бесконечно много прямых.
Cлайд 4
Укажите номера верных утверждений * 1.Если угол равен 56⁰, то вертикальный с ним угол равен 124⁰. 2.Существует точка плоскости, через которую можно провести бесконечное количество различных прямых. 3.Через любую точку плоскости можно провести не более двух прямых.
Cлайд 5
* Сформулируйте свойство вертикальных углов. Сколько прямых можно провести через точку на плоскости? Вертикальные углы равны Через точку на плоскости можно провести бесконечно много прямых.
Cлайд 6
Укажите номера верных утверждений * 1.Любые три различные прямые проходят через одну общую точку. 2.Существует точка плоскости, не лежащая на данной прямой, через которую нельзя провести на плоскости ни одной прямой, параллельной данной. 3.Если угол равен 47⁰, то смежный с ним угол равен 133⁰.
Cлайд 7
* Как могут взаимно располагаться три прямых на плоскости? Сформулируйте аксиому параллельных прямых. Сформулируйте свойство смежных углов. Три прямых на плоскости могут иметь одну общую точку, могут пересекаться попарно, могут и не иметь общих точек Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Сумма смежных углов равна 180°.
Cлайд 8
Укажите номера верных утверждений * 1.Через любые две различные точки плоскости можно провести не более одной прямой. 2.Через любые две различные точки плоскости можно провести не менее одной прямой. 3.Если угол равен 54⁰, то вертикальный с ним угол равен 36⁰.
Cлайд 9
* Сформулируйте аксиому о взаимном расположении прямой и точек на плоскости. Сформулируйте свойство вертикальных прямых Вертикальные углы равны. Через любые две точки проходит прямая, и притом только одна.
Cлайд 10
Укажите номера верных утверждений * 1.Через любую точку плоскости можно провести прямую. 2.Через любую точку плоскости можно провести единственную прямую. 3.Существует точка плоскости, через которую можно провести прямую.
Cлайд 11
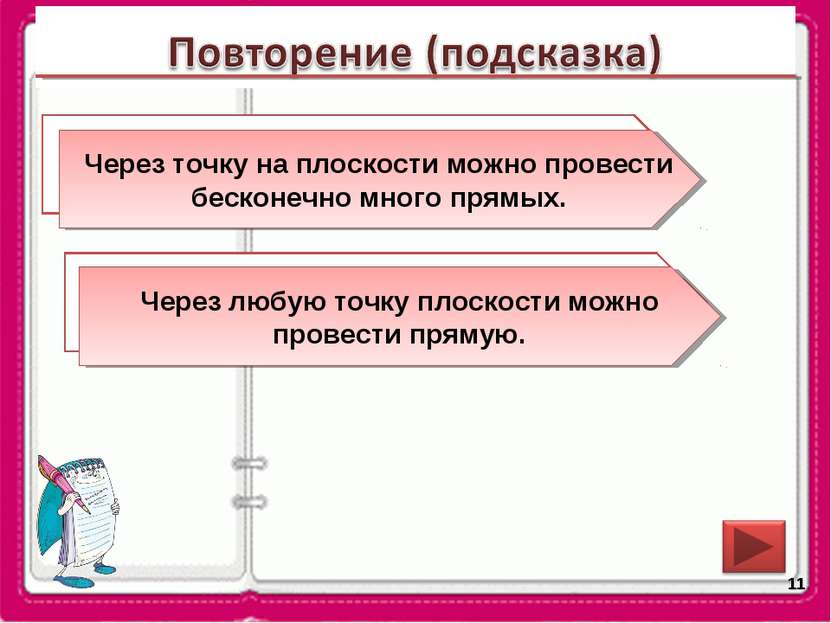
* Сколько прямых можно провести через точку на плоскости? Через точку на плоскости можно провести бесконечно много прямых. Существует ли точка плоскости, через которую нельзя провести прямую? Через любую точку плоскости можно провести прямую.
Cлайд 12
Укажите номера верных утверждений * 1.Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны. 2.Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 90⁰ 3.Если при пересечении двух прямых третьей соответственные углы равны, то прямые перпендикулярны.
Cлайд 13
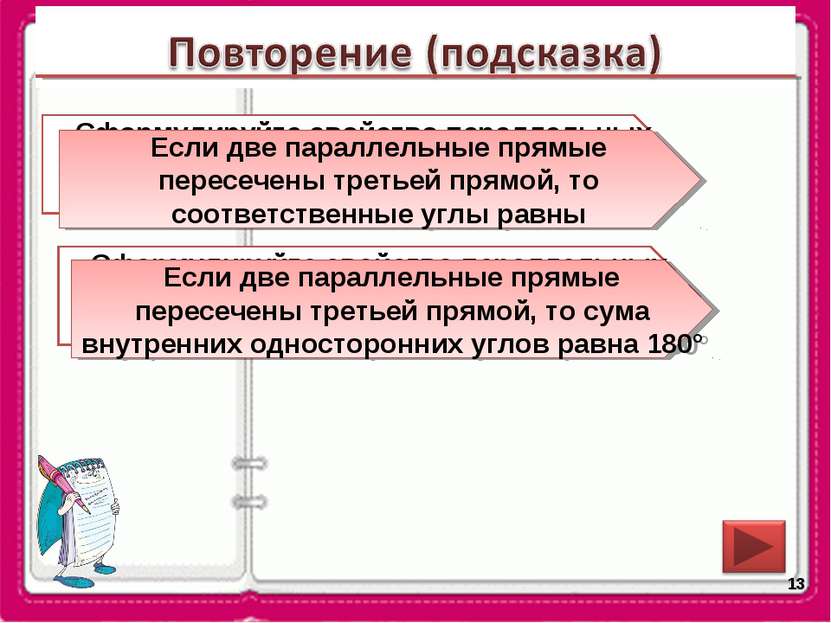
* Сформулируйте свойство параллельных прямых относительно соответственных углов Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны Сформулируйте свойство параллельных прямых относительно внутренних односторонних углов. Если две параллельные прямые пересечены третьей прямой, то сума внутренних односторонних углов равна 180°
Cлайд 14
Укажите номера верных утверждений * 1.Если при пересечении двух прямых третьей сумма внутренних накрест лежащих углов равна 180⁰, то прямые параллельны 2.Если при пересечении двух прямых третьей соответственные углы равны 75⁰ и 105⁰, то прямые параллельны 3.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180⁰, то прямые параллельны
Cлайд 15
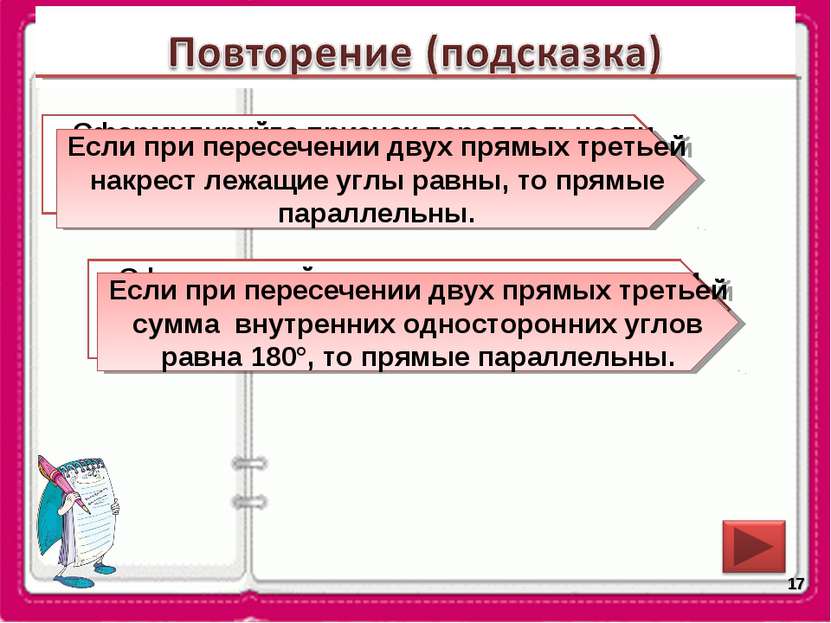
* Сформулируйте признак параллельности двух прямых относительно накрест лежащих углов. Сформулируйте признак параллельности двух прямых относительно соответственных углов. Сформулируйте признак параллельности двух прямых относительно внутренних односторонних углов. Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Cлайд 16
Укажите номера верных утверждений * 1.Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны 45⁰, то прямые параллельны. 2.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180⁰, то прямые перпендикулярны. 3.Если две перпендикулярные прямые пересечены прямой, то внутренние накрест лежащие углы равны.
Cлайд 17
* Сформулируйте признак параллельности двух прямых относительно накрест лежащих углов. Сформулируйте признак параллельности двух прямых относительно внутренних односторонних углов. Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Cлайд 18
Укажите номера верных утверждений * 1.Если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы равны. 2.Если при пересечении двух прямых третьей сумма соответственных углов равна 180⁰, то прямые параллельны. 3.Если две прямые перпендикулярны третьей прямой, то прямые параллельны.
Cлайд 19
* Сформулируйте следствие из аксиомы параллельных прямых и обратное следствию утверждение Сформулируйте признак параллельности двух прямых относительно соответственных углов. Сформулируйте признак параллельности двух прямых относительно внутренних односторонних углов. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перепендикулярна и к другой. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Cлайд 20
Укажите номера верных утверждений * 1.Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны. 2.Если при пересечении двух прямых третьей внутренние односторонние углы равны 70⁰, то прямые параллельны. 3.Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны 39⁰ и 141⁰, то прямые параллельны.
Cлайд 21
* Сформулируйте признак параллельности двух прямых относительно накрест лежащих углов. Сформулируйте признак параллельности двух прямых относительно внутренних односторонних углов. Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Cлайд 22
Укажите номера верных утверждений * 1.Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие тр-ки подобны. 2.Если один из острых углов прямоугольного треугольника равен 25⁰, то другой угол равен 65⁰. 3.Если гипотенуза и катет одного прямоугольного тр-ка соответственно равны гипотенузе и катету другого прямоугольного тр-ка, то тр-ки равны
Cлайд 23
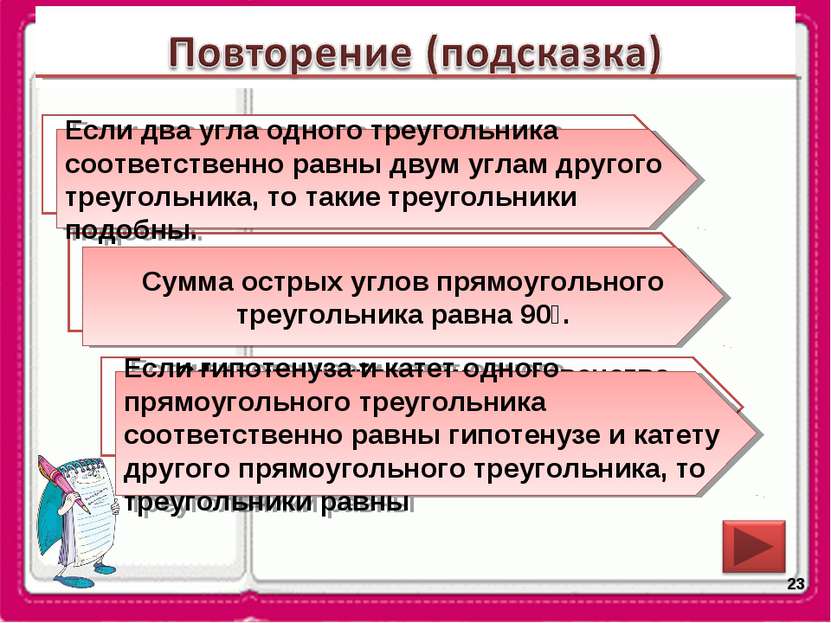
* Сформулируйте признак треугольника по углам Каким свойством обладают острые угла прямоугольного треугольника? Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Сумма острых углов прямоугольного треугольника равна 90⁰. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то треугольники равны
Cлайд 24
Укажите номера верных утверждений * 1.Если в ∆АВС углы А и В соответственно равны 36⁰ и 64⁰, то внешний угол этого треугольника при вершине С равен 100⁰. 2.Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны 3.Если один из острых углов прямоугольного треугольника равен 20⁰, то дугой угол равен 80⁰.
Cлайд 25
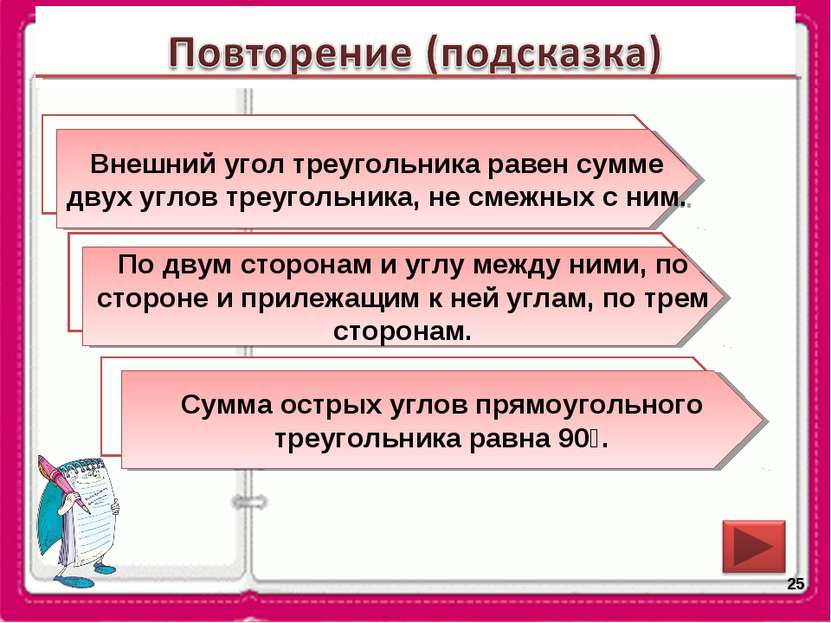
* Каким свойством обладает внешний угол треугольника? По каким элементам можно определить равенство треугольников? Сформулируйте свойство острых углов прямоугольного треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. По двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам. Сумма острых углов прямоугольного треугольника равна 90⁰.
Cлайд 26
Укажите номера верных утверждений * 1.Если в ∆АВС углы А и В равны соответственно 40⁰ и 70⁰, то внешний угол этого треугольника при вершине С равен 70⁰. 2.Внешний угол треугольника равен сумме внутренних углов, не смежных с ним. 3.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Cлайд 27
* Чему равен внешний угол треугольника? Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Сформулируйте признак равенства треугольников по двум сторонам и углу между ними. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Cлайд 28
Укажите номера верных утверждений * 1.Сумма углов прямоугольного треугольника равна 90⁰. 2.Любые два прямоугольных треугольника подобны. 3.Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Cлайд 29
* Чему равна сумма углов треугольника? Когда прямоугольные треугольники могут быть подобны? Сформулируйте признак равенства прямоугольных треугольников по катету и острому углу. Сумма углов треугольника равна 180⁰. Прямоугольные треугольники могут быть подобными, если выполняется один из признаков подобия треугольников. Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Cлайд 30
Укажите номера верных утверждений * 1.Если один из углов равнобедренного треугольника равен 30⁰, то другой его угол равен 120⁰. 2.Если три стороны одного треугольника соответственно в 5 раз больше трех сторон другого треугольника, то такие треугольники подобны. 3.Сумма углов прямоугольного треугольника равна 180⁰.
Cлайд 31
* Какие углы в равнобедренном треугольнике равны? Сформулируйте признак подобия треугольников по трем сторонам. Чему равна сумма углов треугольника? В равнобедренном треугольнике углы при основании равны. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны. Сумма углов треугольника равна 180⁰?
Cлайд 32
Укажите номера верных утверждений * 1.В∆АВС, для которого ∠А=45⁰, ∠В=55⁰, ∠80⁰, сторона АС – наименьшая. 2.Квадрат любой стороны треугольника равен сумме квадратов других сторон треугольника без удвоенного произведения этих сторон на косинус угла между ними. 3.В треугольнике против меньшей стороны лежит меньший угол.
Cлайд 33
* Сформулируйте теорему о соотношениях между сторонами и углами треугольника. Сформулируйте теорему косинусов. В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона. Квадрат любой стороны треугольника равен сумме квадратов других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Cлайд 34
Укажите номера верных утверждений * 1.Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам 2.В треугольнике АВС, для которого ∠А=40⁰, ∠В=55⁰, ∠85⁰, сторона АС – наименьшая. 3.Каждая сторона треугольника меньше суммы других сторон.
Cлайд 35
* В какой точке лежит центр вписанной в треугольник окружности? Сформулируйте неравенство треугольника. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис углов треугольника. Сформулируйте теорему о соотношениях между сторонами и углами треугольника. В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона. Каждая сторона треугольника меньше суммы двух других сторон.
Cлайд 36
Укажите номера верных утверждений * 1. 1.Центром окружности, вписанной в правильный треугольник, является точка пересечения серединных перпендикуляров к его сторонам. 2.В любой прямоугольный треугольник можно вписать окружность. 3.Центр окружности, описанного около прямоугольного треугольника, находится на катете этого треугольника.
Cлайд 37
* В какой точке лежат центры вписанной в правильный треугольник окружности и описанной окружности около этого же треугольника? В какой треугольник можно вписать окружность? Где лежит центр окружности, описанной около прямоугольного треугольника? Центры таких окружностей совпадают и лежат в точке пересечения серединных перпендикуляров к сторонам треугольника. В любой треугольник можно вписать окружность, а значит и прямоугольный? Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы прямоугольного треугольника.
Cлайд 38
Укажите номера верных утверждений * 1.Центром окружности, описанной около треугольника, является точка пересечения его биссектрис. 2.В треугольнике АВС, для которого ∠А=44⁰, ∠В=55⁰, ∠81⁰, сторона ВС – наибольшая. 3.Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров, проведенных у его сторонам.
Cлайд 39
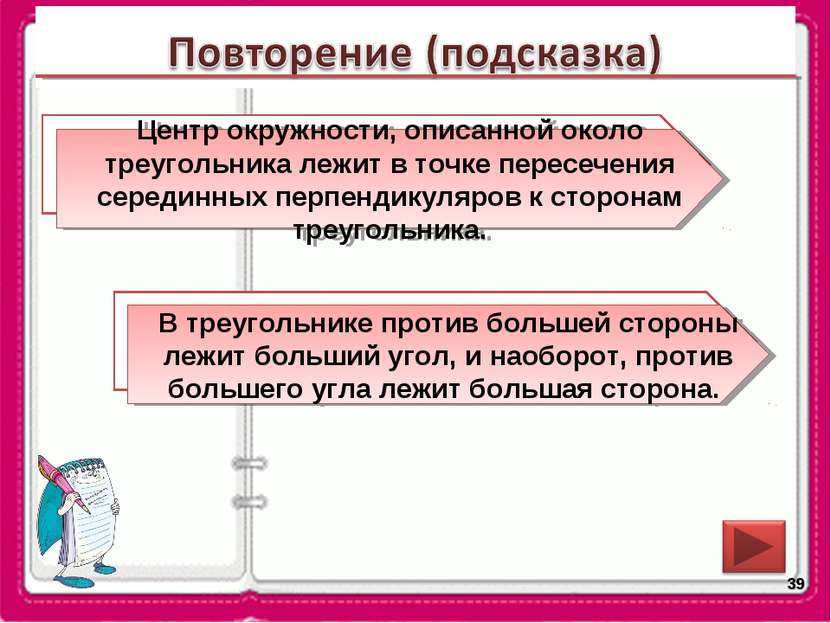
* В какой точке лежит центр окружности, описанной около треугольника? Центр окружности, описанной около треугольника лежит в точке пересечения серединных перпендикуляров к сторонам треугольника. Сформулируйте теорему о соотношениях между сторонами и углами треугольника. В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.
Cлайд 40
Укажите номера верных утверждений * 1.В треугольнике против меньшего угла лежит большая сторона. 2.Центром окружности, описанной около правильного треугольника, является точка пересечения его биссектрис. 3.Кажддая сторона треугольника больше суммы двух других сторон.
Cлайд 41
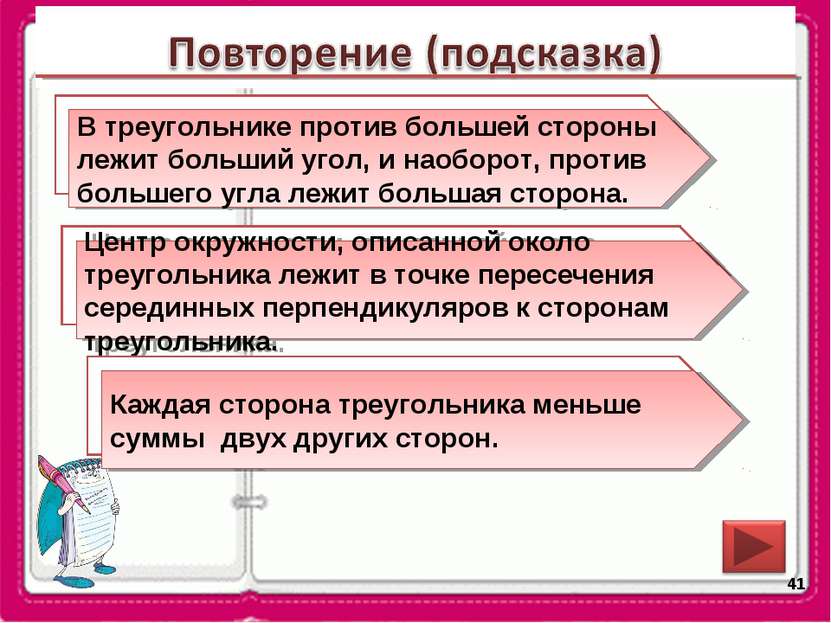
* Сформулируйте теорему о соотношениях между сторонами и углами треугольника. В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона. В какой точке лежит центр окружности, описанной около треугольника? Центр окружности, описанной около треугольника лежит в точке пересечения серединных перпендикуляров к сторонам треугольника. Сформулируйте неравенство треугольника. Каждая сторона треугольника меньше суммы двух других сторон.
Cлайд 42
Укажите номера верных утверждений * 1.В любой квадрат можно вписать окружность. 2.Если диагональ четырехугольника делит его углы пополам, то этот четырехугольник – ромб. 3.В любой четырехугольник можно вписать окружность.
Cлайд 43
* В какой четырехугольник можно вписать окружность? Сформулируйте признак ромба. В какой четырехугольник можно вписать окружность? В четырехугольник, суммы противоположных сторон которого равны можно вписать окружность, значит в квадрат можно вписать окружность. Если диагональ четырехугольника перпендикулярны и делят углы четырехугольника пополам, то этот четырехугольник – ромб. В четырехугольник можно вписать окружность, если суммы противоположных углов равны 180⁰
Cлайд 44
Укажите номера верных утверждений * 1.Сумма двух противоположных углов параллелограмма равна 180⁰. 2.Если в четырехугольник можно вписать окружность, то сумма его противоположных сторон равна 200, а длина третьей стороны равна 60, то длина оставшейся стороны равна 140. 3.Около любого четырехугольника можно описать окружность.
Cлайд 45
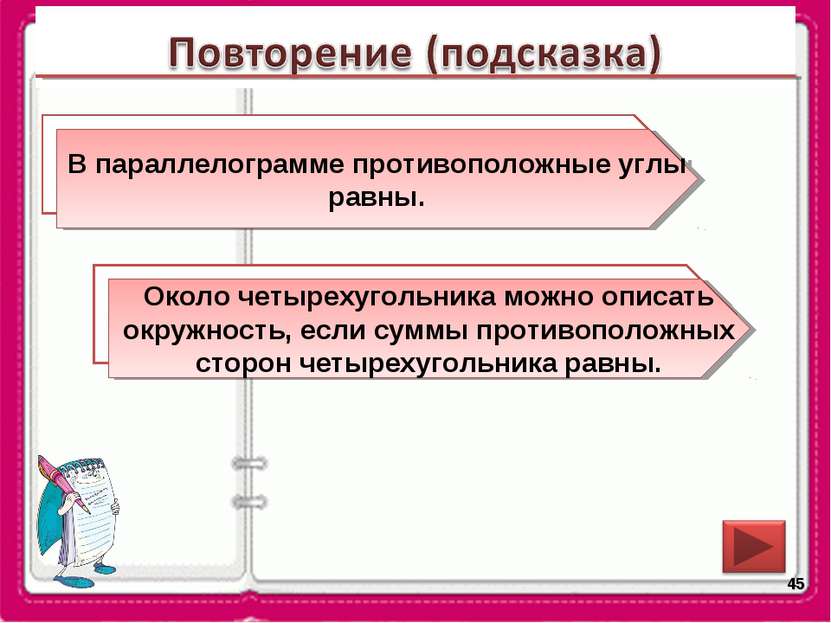
* Сформулируйте свойство углов параллелограмма. Около какой четырехугольника можно описать окружность? В параллелограмме противоположные углы равны. Около четырехугольника можно описать окружность, если суммы противоположных сторон четырехугольника равны.
Cлайд 46
Укажите номера верных утверждений * 1.Около любого квадрата можно описать окружность. 2.Сумма двух противоположных углов вписанного в окружность четырехугольника равна 90⁰. 3.Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
Cлайд 47
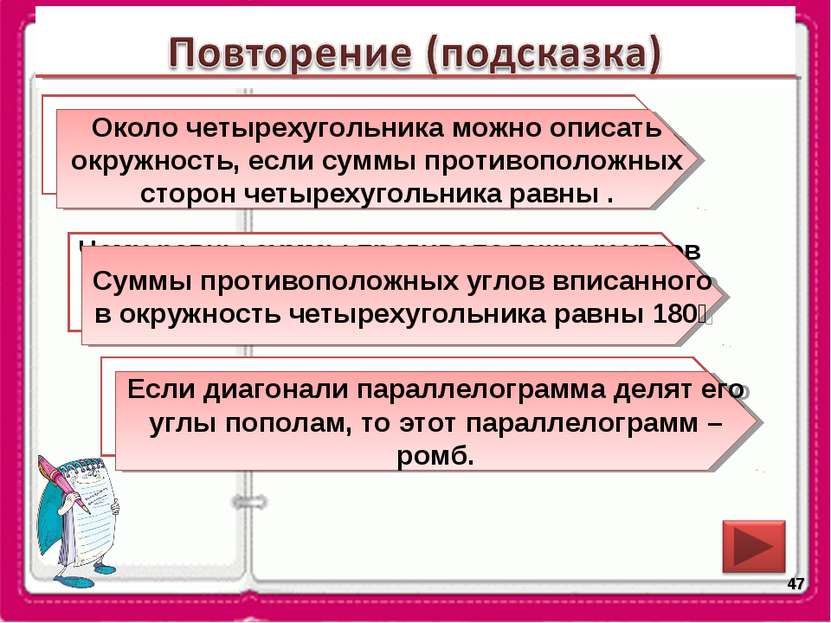
* Чему равны суммы противоположных углов вписанного в окружность четырехугольника? Сформулируйте признак ромба с учетом того, что ромб – это параллелограмм. Около какой четырехугольника можно описать окружность? Около четырехугольника можно описать окружность, если суммы противоположных сторон четырехугольника равны . Суммы противоположных углов вписанного в окружность четырехугольника равны 180⁰ Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
Cлайд 48
Укажите номера верных утверждений * 1.Если в четырехугольнике диагонали равны, то этот четырехугольник – прямоугольник. 2.Если в четырехугольник можно вписать окружность, сумма длин двух его противоположных сторон равна 180, а длина третьей стороны равна 70, то длина оставшейся стороны равна 110. 3.Диагонали прямоугольника равны.
Cлайд 49
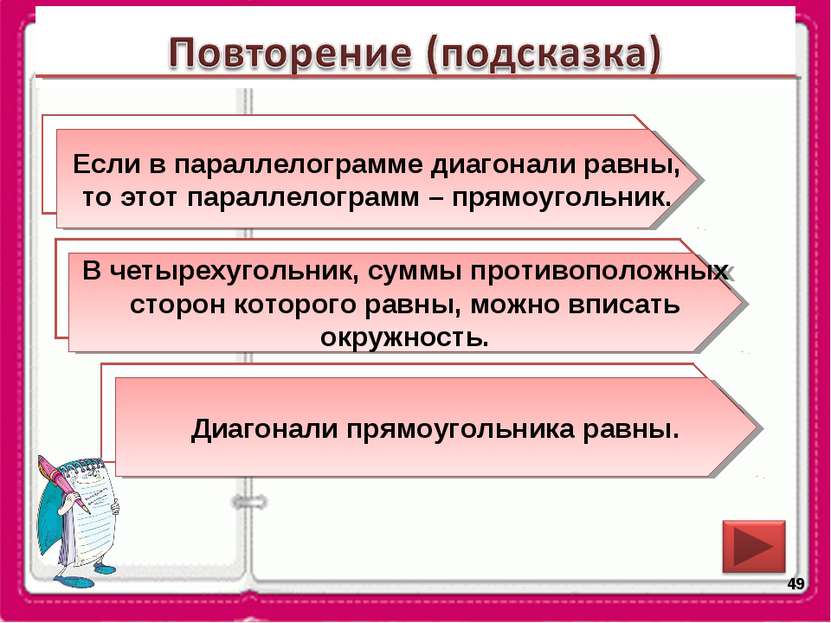
* Сформулируйте признак прямоугольника. Каким особым свойством обладает прямоугольник? Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. В какой четырехугольник можно вписать окружность? В четырехугольник, суммы противоположных сторон которого равны, можно вписать окружность. Диагонали прямоугольника равны.
Cлайд 50
Укажите номера верных утверждений * 1.В любой ромб можно вписать окружность. 2.Около любой трапеции можно описать окружность. 3.Если сумма двух противоположных углов четырехугольника равна 90, около этого четырехугольника можно описать окружность
Cлайд 51
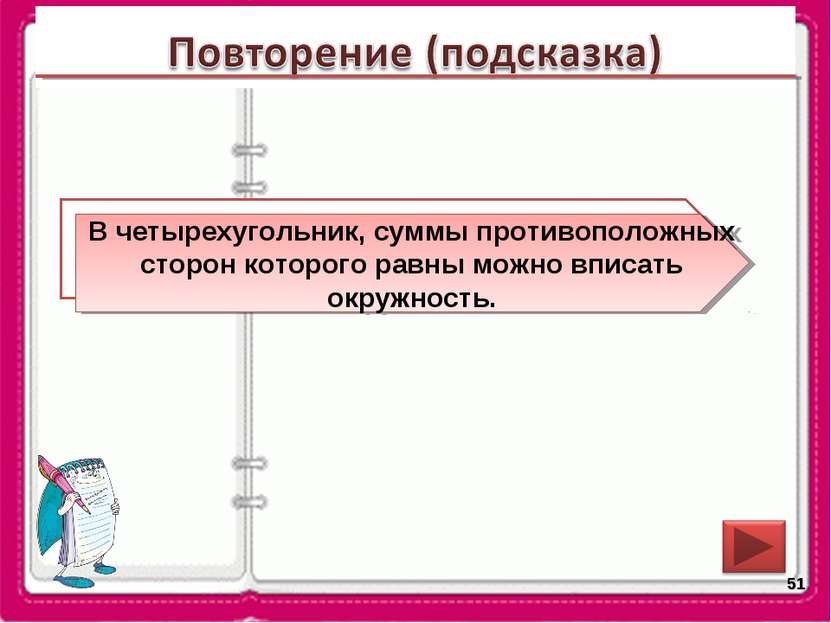
* В какой четырехугольник можно вписать окружность? В четырехугольник, суммы противоположных сторон которого равны можно вписать окружность.
Cлайд 52
Укажите номера верных утверждений * 1.Площадь круга радиуса R равна πR². 2.Если радиус окружности равен 10, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются. 3.Длина окружности радиуса R равна πR.
Cлайд 53
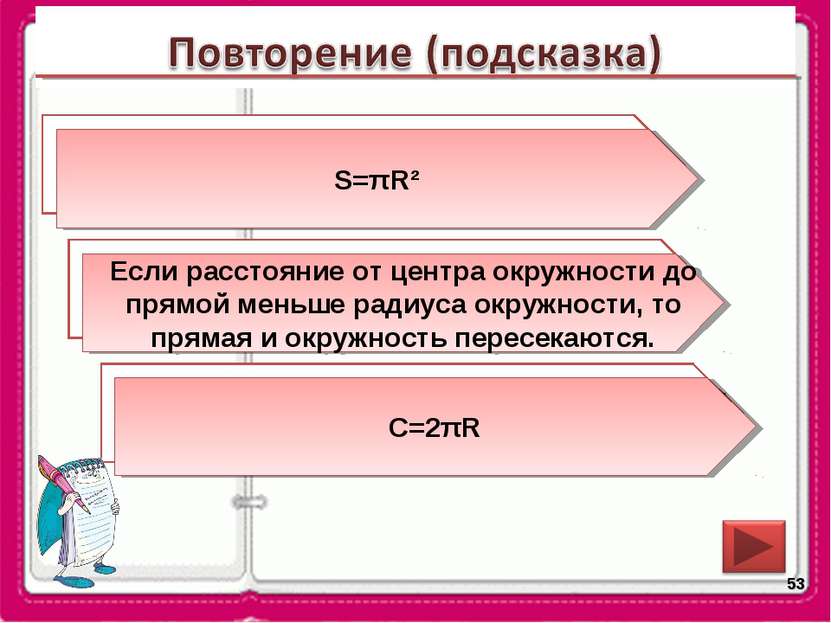
* По какой формуле можно вычислить площадь круга? При каком условии прямая и окружность пересекаются? По какой формуле можно вычислить длину окружности? S=πR² Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются. С=2πR
Cлайд 54
Укажите номера верных утверждений * 1.Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 6 , то эти окружности не имеют общих точек 2.Если радиус окружности равна 3, а расстояние от центра окружности до прямой равно 2, эти прямая и окружность не имеют общих точек. 3.Через любые три различные точки плоскости, не лежащие на одной прямой, можно провести не более одной окружности
Cлайд 55
* Каково взаимное положение двух окружностей, если расстояние между их центрами больше суммы их радиусов? Можно ли через три точки плоскости провести окружность? Если расстояние между центрами двух окружностей больше суммы их радиусов, то окружности не пересекаются. При каком условии прямая и окружность не пересекаются? Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не пересекаются. Через три точки плоскости можно провести окружность, если центр окружности лежит на биссектрисе угла, вершина которого лежит в одной из данных точек, стороны этого угла проходят через две другие точки, и центр окружности равноудален от данных точек. Значит такая окружность единственная.
Cлайд 56
Укажите номера верных утверждений * 1.Если расстояние между центрами двух окружностей меньше суммы их радиусов, то эти окружности пересекаются. 2.Площадь круга радиуса R равна 2πR. 3.Длина окружности радиуса R равна 2πR.
Cлайд 57
* Каково взаимное положение двух окружностей, если расстояние между их центрами меньше суммы их радиусов? Если расстояние между центрами двух окружностей меньше суммы их радиусов, то окружности пересекаются. По какой формуле можно вычислить площадь круга? S=πR² По какой формуле можно вычислить длину окружности? С=2πR
Cлайд 58
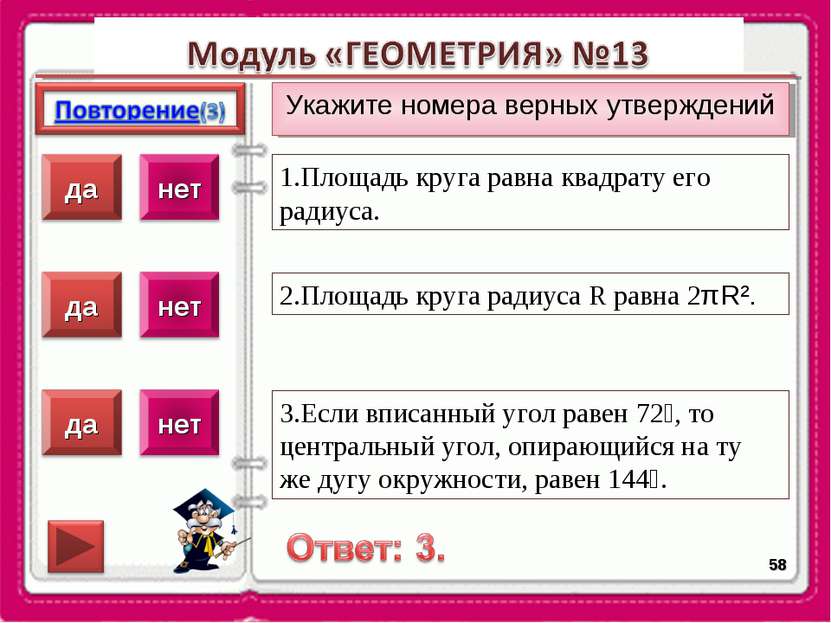
Укажите номера верных утверждений * 1.Площадь круга равна квадрату его радиуса. 2.Площадь круга радиуса R равна 2πR². 3.Если вписанный угол равен 72⁰, то центральный угол, опирающийся на ту же дугу окружности, равен 144⁰.
Cлайд 59
* Чему равна градусная мера вписанного угла? Чему равна градусная мера центрального угла? По какой формуле можно вычислить площадь круга? S=πR² Градусная мера вписанного угла равна половине дуги, на которую он опирается. Градусная мера центрального угла равна дуге, на которую он опирается.
Cлайд 60
Укажите номера верных утверждений * 1.Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности не имеют общих точек. 2.Если расстояние между центрами двух окружностей больше суммы их радиусов, то эти окружности пересекаются. 3.Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти прямая и окружность пересекаются.
Cлайд 61
* Каково взаимное положение двух окружностей, если расстояние между их центрами меньше суммы их радиусов? Если расстояние между центрами двух окружностей меньше суммы их радиусов, то окружности пересекаются. При каком условии прямая и окружность пересекаются? Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются. Каково взаимное положение двух окружностей, если расстояние между их центрами больше суммы их радиусов? Если расстояние между центрами двух окружностей больше суммы их радиусов, то окружности не пересекаются.
Cлайд 62
Автор шаблона Ермолаева Ирина Алексеевна учитель информатики и математики МОУ «Павловская сош» с.Павловск Алтайский край http://www.uchportal.ru/load/160-1-0-18319 «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013. http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg http://www.grafamania.net/uploads/posts/2009-07/thumbs/1246640277_001.jpg
