X
Код презентации скопируйте его
ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)
Скачать эту презентацию
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)
Скачать эту презентациюCлайд 1
Автор презентации: Гладунец Ирина Владимировна Учитель математики МБОУ гимназия №1 г.Лебедянь Липецкой области *
Cлайд 2
Повторение (2) Ответ: 4. Найти АС. * В С А 5 ⇒ ⇒ По теореме Пифагора
Cлайд 3
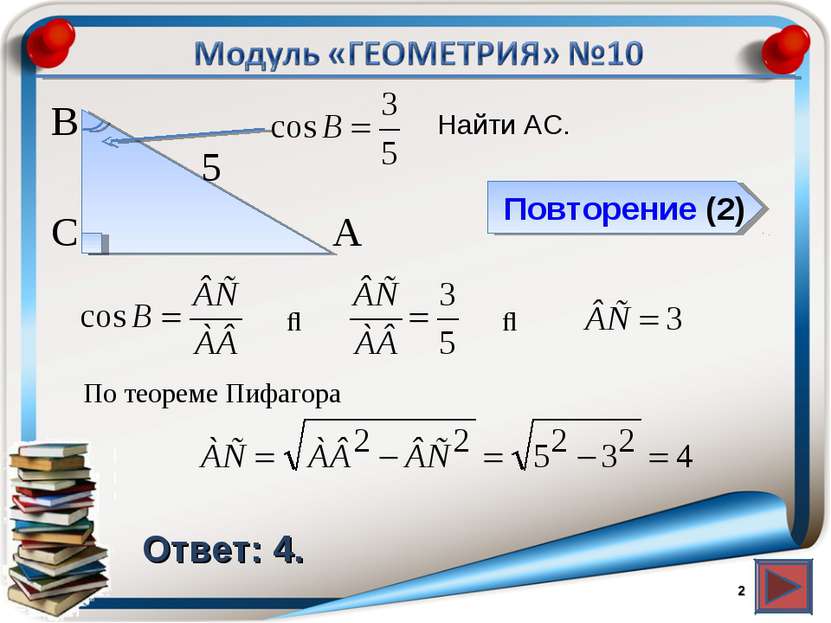
* Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Cлайд 4
Повторение (2) Ответ: 17. * Найти АВ. В С А 15 ⇒ ⇒ По теореме Пифагора
Cлайд 5
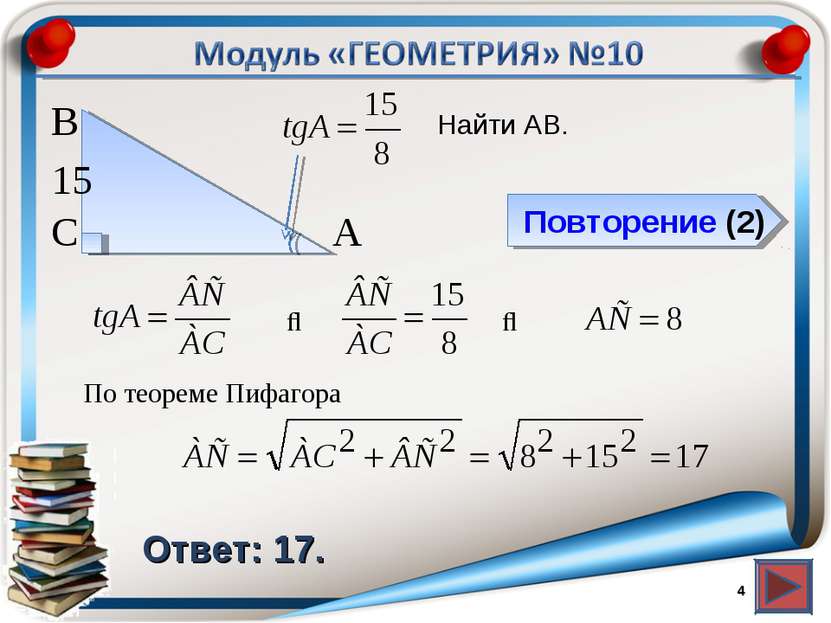
* Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Cлайд 6
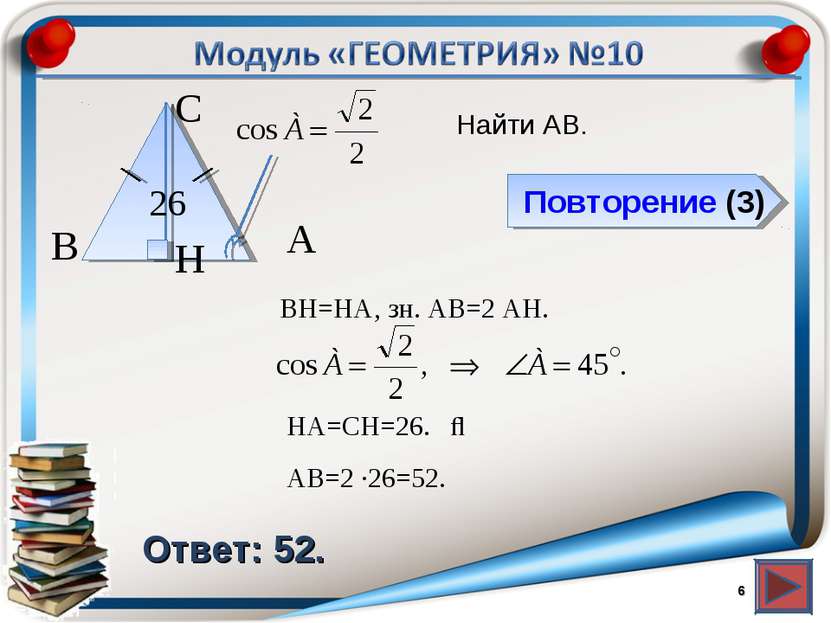
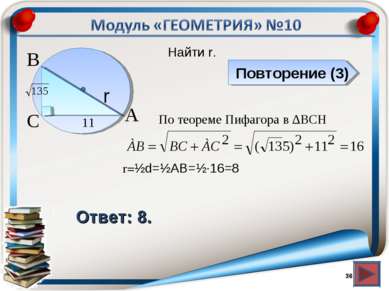
Повторение (3) Ответ: 52. Найти АВ. * В С А 26 BH=HA, зн. АВ=2 AH. H ⇒ HA=СH=26. АВ=2 ∙26=52.
Cлайд 7
* Высота в равнобедренном треугольнике, проведенная к основанию, является и медианой В прямоугольном треугольнике сумма острых углов равна 90⁰ Если в треугольнике два угла равны, то такой треугольник равнобедренный
Cлайд 8
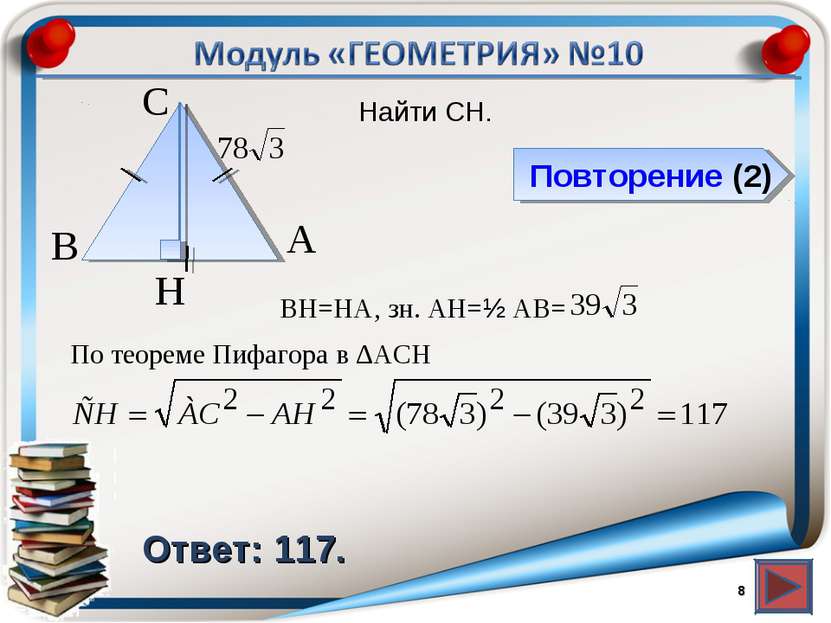
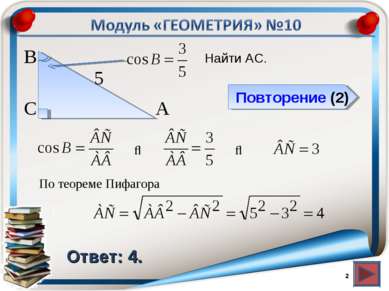
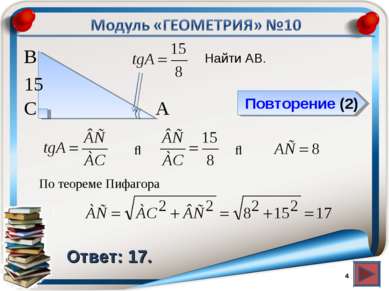
Повторение (2) Ответ: 117. Найти CH. * В А H С BH=HA, зн. АH=½ AB= По теореме Пифагора в ∆ACH
Cлайд 9
* Высота в равнобедренном треугольнике, проведенная к основанию, является и медианой В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Cлайд 10
Повторение (3) Ответ: 75. Найти AB. * В А H С 120⁰ Проведем высоту CH, получим ∆ВCH. ∠ВCH=60⁰ ⇒ ∠CВH=30⁰ ⇒ По теореме Пифагора в ∆BCH
Cлайд 11
* Высота в прямоугольном треугольнике, проведенная к основанию является биссектрисой и медианой В прямоугольном треугольнике катет, лежащий против угла в 30⁰, равен половине гипотенузы В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Cлайд 12
Повторение (4) Ответ: 5. Дано: параллелограмм, P=10, АЕ:ЕD=1:3. Найти AD * В А D С Е 1 2 3 ∠1=∠3 как накрест лежащие при секущей ВЕ ∠3=∠2 так как ∠1=∠2 по условию ⇒ АВ=АЕ Пусть АЕ=х, тогда АВ=х, ЕD=3х Р=2∙(х+3х) ⇒ 2∙(х+3х)=10 4х=5 Х=1,25 AD=4∙1,25=5
Cлайд 13
* Биссектриса – это луч, который делит угол пополам Периметр многоугольника – это сумма длин всех сторон многоугольника При пересечении двух параллельных прямых накрест лежащие углы равны Если два угла в треугольнике равны, то треугольник - равнобедренный
Cлайд 14
Повторение (2) Ответ: 66. АВСD – прямоугольник, ∠1:∠2=1:2. Найти АС. * В А D С 33 1 2 ∠1=⅓ ∠ВАС ⇒ ∠1=⅓ ∙90⁰=30⁰ ⇒ СD=½АС ⇒ АС=2 СD= 66
Cлайд 15
* Прямоугольник – это параллелограмм с прямыми углами Катет, лежащий против угла в 30⁰, равен половине гипотенузы
Cлайд 16
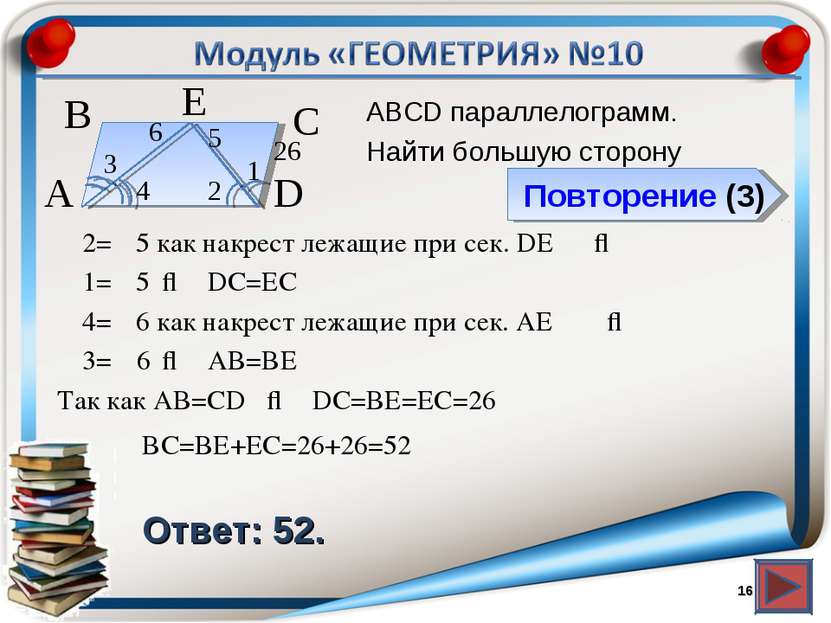
Повторение (3) Ответ: 52. АВСD параллелограмм. Найти большую сторону * 2 3 4 1 26 В А D С ∠2=∠5 как накрест лежащие при сек. DЕ ∠4=∠6 как накрест лежащие при сек. АЕ ⇒ DC=ЕC Е 6 5 ⇒ ⇒ ∠1=∠5 АВ=ВЕ ⇒ ∠3=∠6 DC=ВЕ=ЕС=26 ⇒ Так как АВ=СD ВC=ВЕ+ЕС=26+26=52
Cлайд 17
* Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны Если в треугольнике два угла равны, то треугольник равнобедренный Если отрезок точкой разделен на части, то его длина равна сумме его частей
Cлайд 18
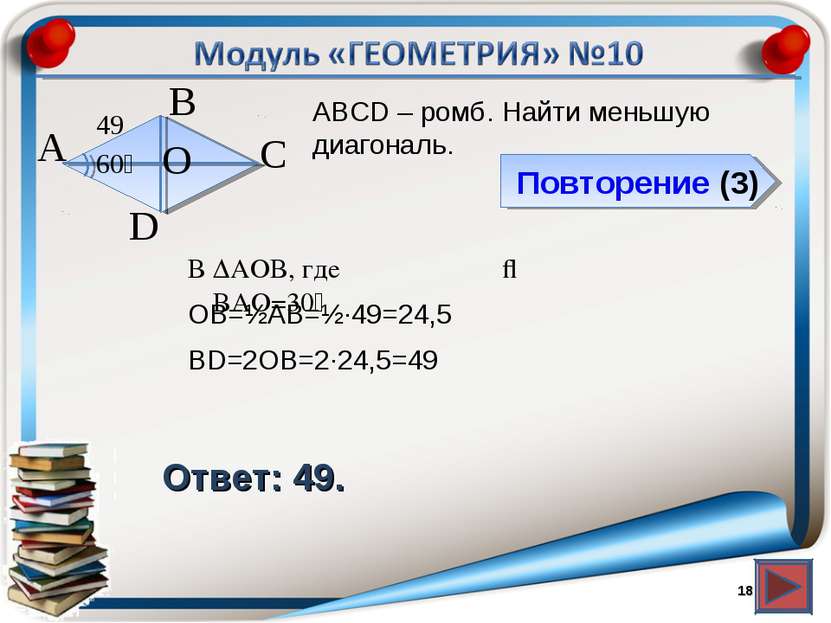
Повторение (3) Ответ: 49. АВСD – ромб. Найти меньшую диагональ. * В А D С 49 60⁰ О В ∆АОВ, где ∠ВАО=30⁰ ⇒ ОВ=½АВ=½∙49=24,5 ВD=2ОВ=2∙24,5=49
Cлайд 19
* Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам Катет прямоугольного треугольника, лежащий против угла в 30⁰ равен половине гипотенузы Диагонали параллелограмма (ромба) точкой пересечения делятся пополам
Cлайд 20
Повторение (3) Ответ: 22. * В А D С 44 12 М К Е ? По теореме Фалеса АЕ=ЕС ⇒ ЕК – средняя линия ∆АСD ⇒ ЕК=½АD=½∙44=22
Cлайд 21
* Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции Параллельные прямые, проведенные через концы равных отрезков на одной из сторон угла, отсекают равные отрезки на другой стороне угла Средняя линия треугольника равна половине третьей стороны треугольника
Cлайд 22
Повторение (3) Ответ: 103. АВСD – трапеция, СЕ||АВ. P∆CDЕ =69. Найти P трапеции * В А D С 34 Е Так как СЕ||АВ, то АВ=ЕС, АЕ=ВС=34 АD=АЕ+ЕD P∆CDЕ =CD+ЕD+СЕ P∆АВCD =АВ+ВС+CD+АD ⇒ P∆АВCD =P∆CDЕ +ВС=69+34=103
Cлайд 23
* Если в четырехугольнике противоположные стороны параллельны, то такой четырехугольник - параллелограмм В параллелограмме противоположные стороны равны Если отрезок точкой разделен на части, то его длина равна сумме его частей
Cлайд 24
Повторение (2) Ответ: 37. АВСD – трапеция * В А D С 29 21 М К ?
Cлайд 25
* Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции Средняя линия трапеции равна полусумме оснований трапеции
Cлайд 26
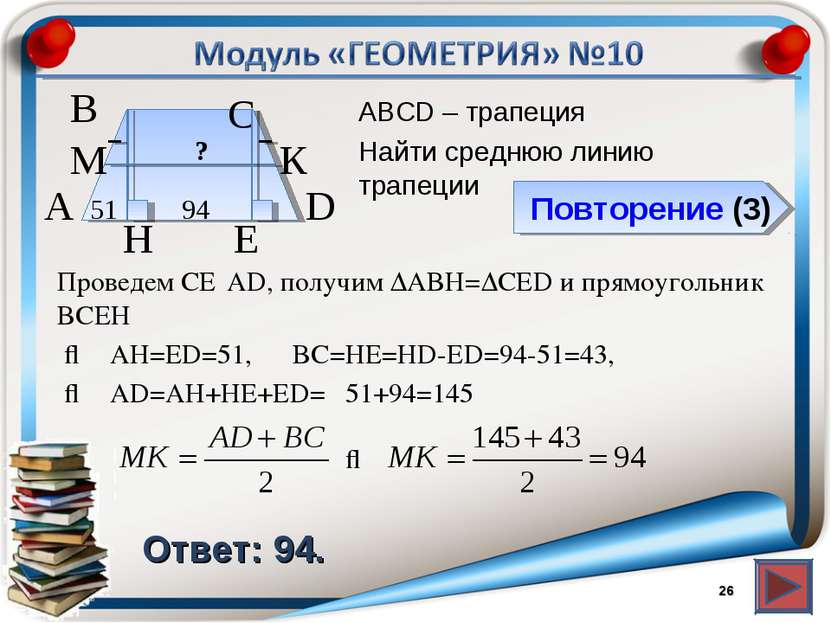
Повторение (3) Ответ: 94. АВСD – трапеция Найти среднюю линию трапеции * В А D С 94 51 H ? К М Проведем СЕ⍊AD, получим ∆ABH=∆CED и прямоугольник BCEH ⇒ AD=AH+HE+ЕD= E 51+94=145 ⇒ AH=ЕD=51, BC=HE=HD-ED=94-51=43, ⇒
Cлайд 27
* Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то треугольники равны Если отрезок точкой разделен на части, то его длина равна сумме длин его частей Средняя линия трапеции равна полусумме оснований трапеции
Cлайд 28
Повторение (3) Ответ: 9,5. E,F – середины диагоналей. Найти EF. * В А D С 34 15 М К Е F ⇒ ME и FK средние линии ∆ABС=∆DВС с общей стороной ВС ME=FK=½BC=½∙15=7,5 EF=MK-ME-FK=24,5-7,5-7,5=9,5
Cлайд 29
* Средняя линия трапеции равна полусумме оснований трапеции Средняя линия треугольника равна половине третьей стороны треугольника Если отрезок точкой разделен на части, то его длина равна сумме длин его частей
Cлайд 30
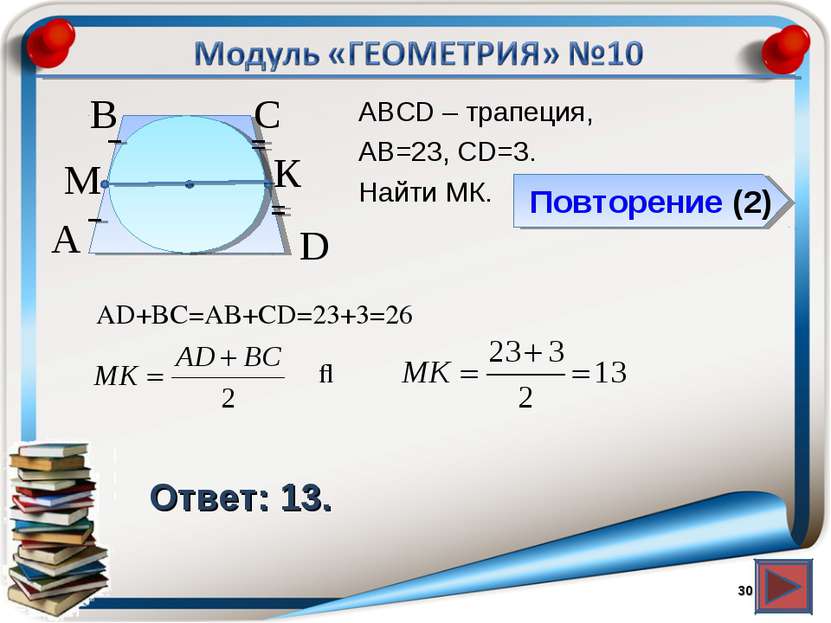
Повторение (2) Ответ: 13. АВСD – трапеция, АВ=23, CD=3. Найти МК. * В А D С М К AD+BC=AB+CD=23+3=26 ⇒
Cлайд 31
* Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны Средняя линия трапеции равна полусумме оснований трапеции
Cлайд 32
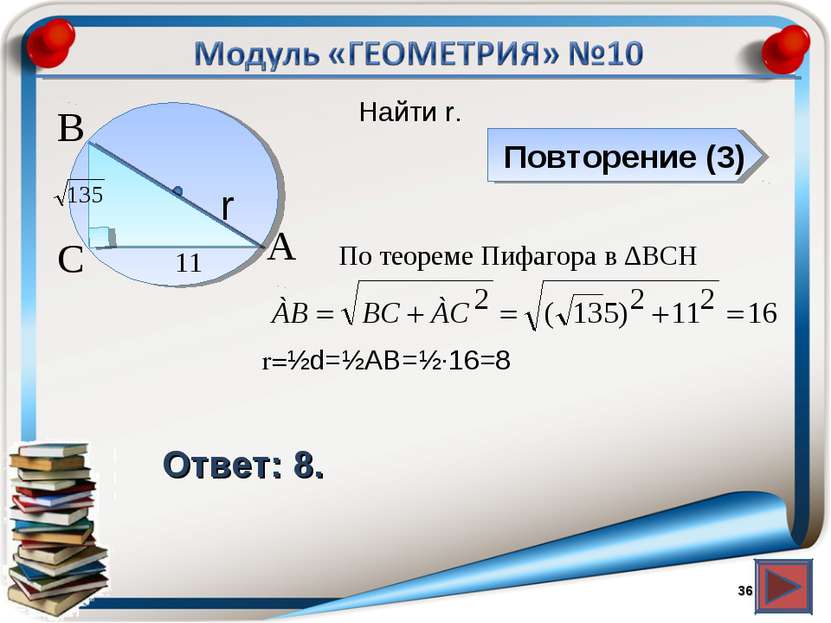
Повторение (3) Ответ: 2,5. АВСD – трапеция, P∆ABCD =100. Найти r. * В А D С r 45 AD+BC=AB+CD=½ P∆ABCD =½∙100 =50 AB=50-CD =50-45=5 r=½d=½AB=½∙5=2,5
Cлайд 33
* Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны Радиус окружности, проведенный в точку касания перпендикулярен касательной Радиус окружности равен половине диаметра
Cлайд 34
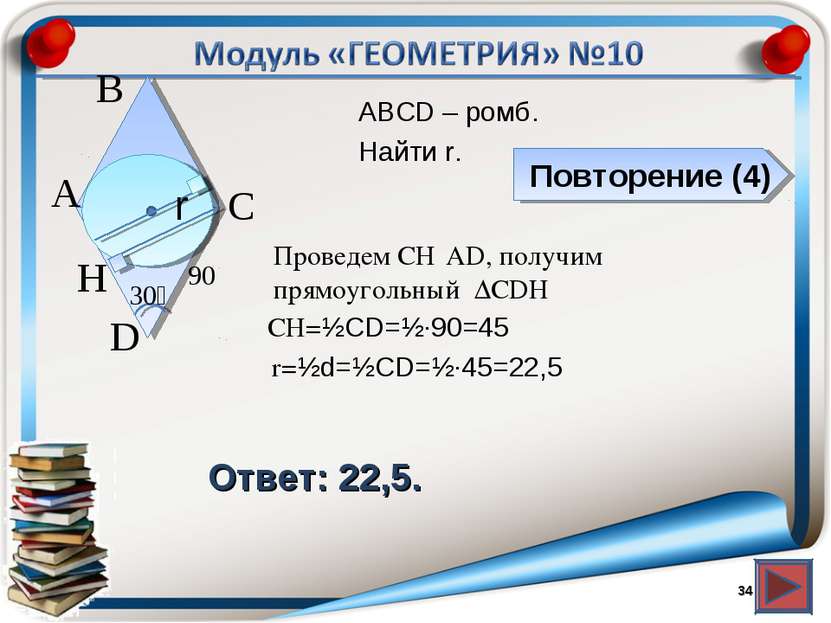
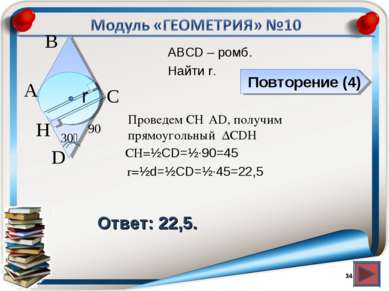Повторение (4) Ответ: 22,5. АВСD – ромб. Найти r. * В А D С r 90 30⁰ Проведем СH⍊AD, получим прямоугольный ∆CDH H CH=½CD=½∙90=45 r=½d=½CD=½∙45=22,5
Cлайд 35
* Радиус окружности, проведенный в точку касания перпендикулярен касательной Перпендикуляры между параллельными прямыми равны В прямоугольном треугольнике катет, лежащий против угла в 30⁰ равен половине гипотенузы Радиус окружности равен половине диаметра
Cлайд 36
Повторение (3) Ответ: 8. Найти r. * В А С r 11 По теореме Пифагора в ∆BCH r=½d=½АВ=½∙16=8
Cлайд 37
* Прямой угол, вписанный в окружность опирается на диаметр окружности В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Радиус окружности равен половине диаметра
Cлайд 38
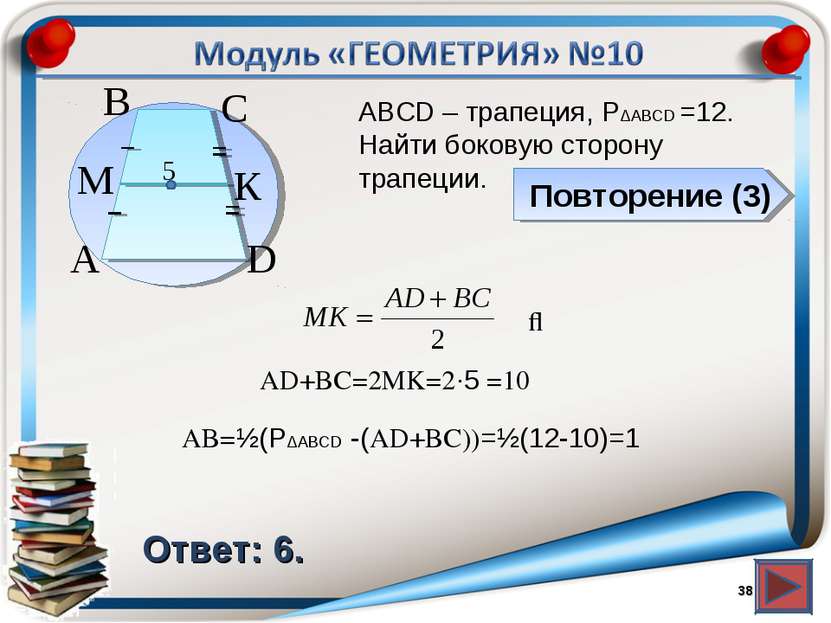
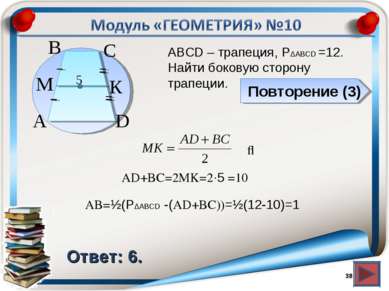Повторение (3) Ответ: 6. АВСD – трапеция, P∆ABCD =12. Найти боковую сторону трапеции. * В А С D К M 5 ⇒ AD+BC=2MK=2∙5 =10 AB=½(P∆ABCD -(AD+BC))=½(12-10)=1
Cлайд 39
* Средняя линия трапеции равна полусумме оснований трапеции Описать окружность можно только около равнобедренной трапеции Периметр многоугольника – это сумма длин всех сторон многоугольника
Cлайд 40
Автор данного шаблона: Ермолаева Ирина Алексеевна учитель информатики и математики МОУ «Павловская сош» с.Павловск Алтайский край http://www.uchportal.ru/load/160-1-0-18316 «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013. *
