X
Код презентации скопируйте его
Решение задач с параметрами
Скачать эту презентацию
Презентация на тему Решение задач с параметрами
Скачать эту презентациюCлайд 1
Решение задач с параметрами Выполнила: Матвиенко Елена Валентиновна – учитель математики ГООУ санаторной школы-интерната г.Петровска Саратовской области.
Cлайд 2
1. Найти все значения параметра а, при которых решением системы является вся прямая. 2. При каких значениях параметра р функция определена при всех хєR ? 3. При каких значениях параметра а система неравенств а) имеет единственное решение; б) не имеет решений; в) имеет бесконечно много решений?
Cлайд 3
1. Найти все значения параметра а, при которых решением системы является вся прямая. Решение. Так как квадратный трехчлен х2-х+1=(х2-2·0,5·х+0,25)+0,75= (х-0,5)2+0,75>0 при любом значении х, то получим систему неравенств: Оцените знаменатель дробей.
Cлайд 4
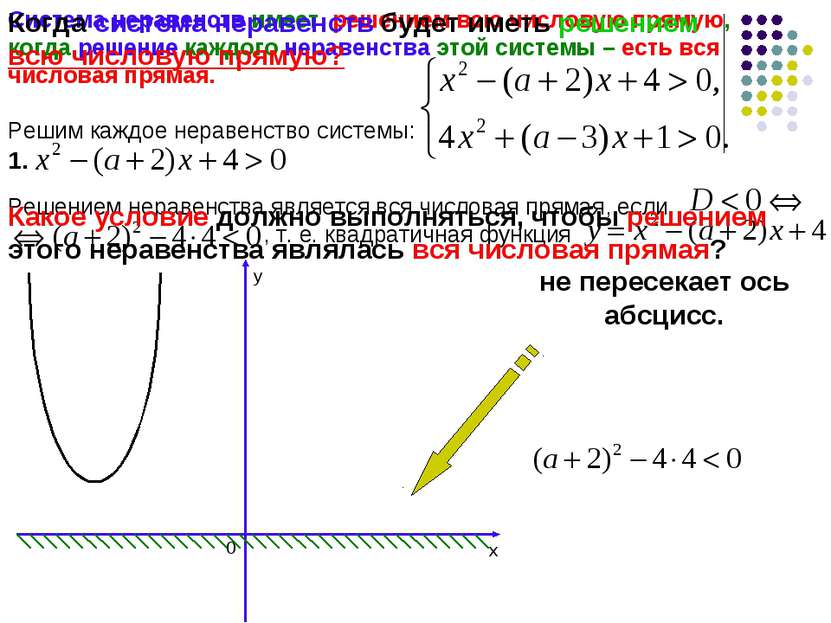
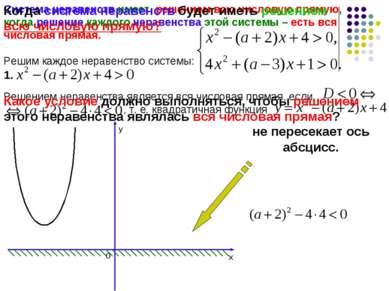Система неравенств имеет решением всю числовую прямую, когда решение каждого неравенства этой системы – есть вся числовая прямая. Решим каждое неравенство системы: 1. Решением неравенства является вся числовая прямая, если , т. е. квадратичная функция не пересекает ось абсцисс. х у 0 Когда система неравенств будет иметь решением всю числовую прямую? Какое условие должно выполняться, чтобы решением этого неравенства являлась вся числовая прямая?
Cлайд 5
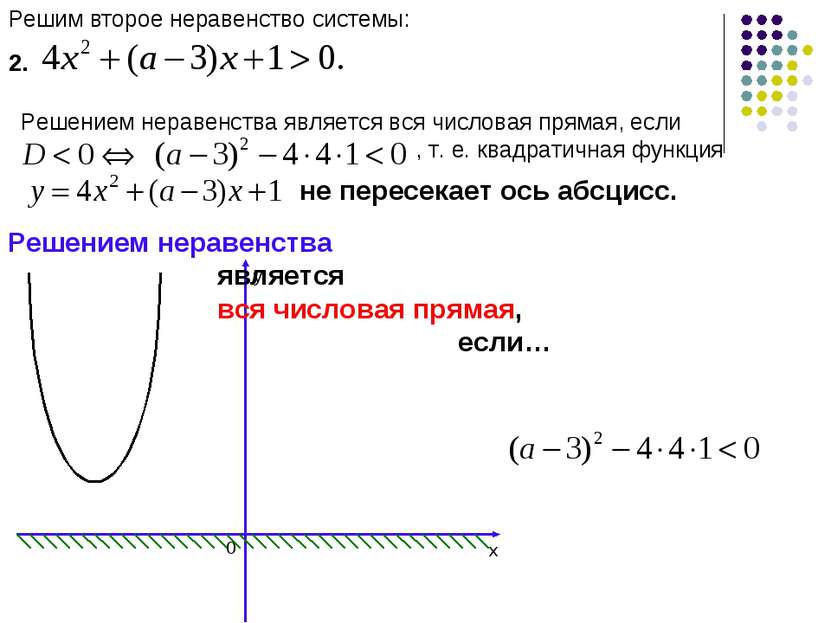
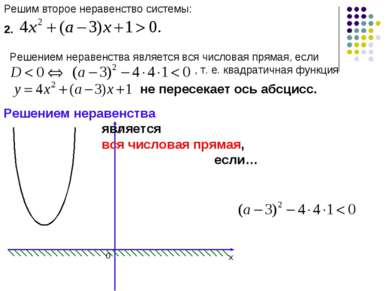Решим второе неравенство системы: 2. Решением неравенства является вся числовая прямая, если , т. е. квадратичная функция не пересекает ось абсцисс. х у 0 Решением неравенства является вся числовая прямая, если…
Cлайд 6
Решим систему неравенств: Ответ: (-1;2).
Cлайд 7
2. При каких значениях параметра р функция определена при всех хєR ? Решение. Область определения функции - множество действительных чисел, удовлетворяющих условию… Какие условия должны выполняться, чтобы решением этого неравенства являлась вся числовая прямая? Ответ:(-∞ ; -1].
Cлайд 8
Домашнее задание: 3. При каких значениях параметра а система неравенств а) имеет единственное решение; б) не имеет решений; в) имеет бесконечно много решений?
