X
Код презентации скопируйте его
Параллельность прямых и плоскостей (10 класс)
Скачать эту презентациюПрезентация на тему Параллельность прямых и плоскостей (10 класс)
Скачать эту презентациюCлайд 2
 Параллельные прямые в пространстве Определение: Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости. Значит, через две параллельные прямые можно провести плоскость и только одну. a ΙΙ b
Параллельные прямые в пространстве Определение: Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости. Значит, через две параллельные прямые можно провести плоскость и только одну. a ΙΙ b
Cлайд 3
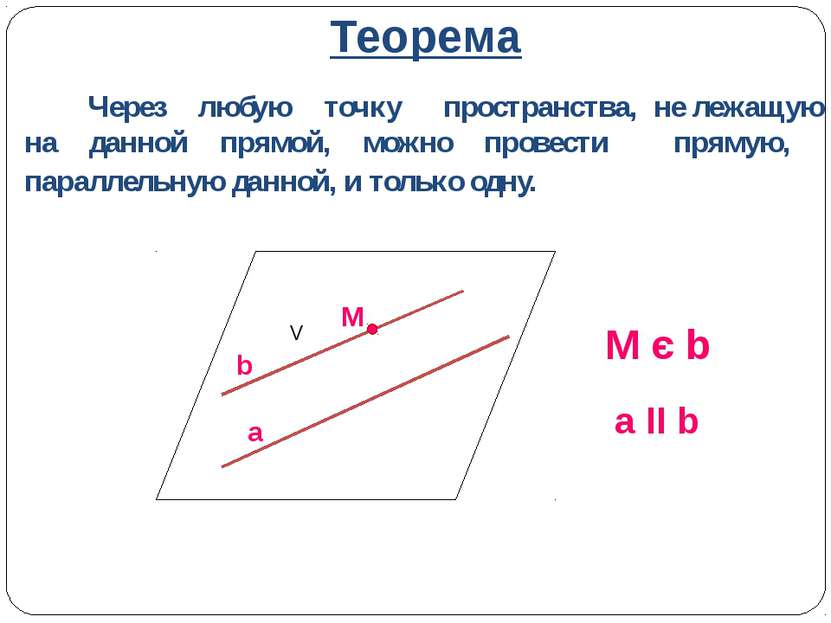
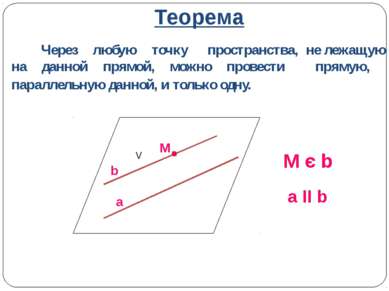 Теорема Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и только одну. M є b a ΙΙ b a V M b
Теорема Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и только одну. M є b a ΙΙ b a V M b
Cлайд 4
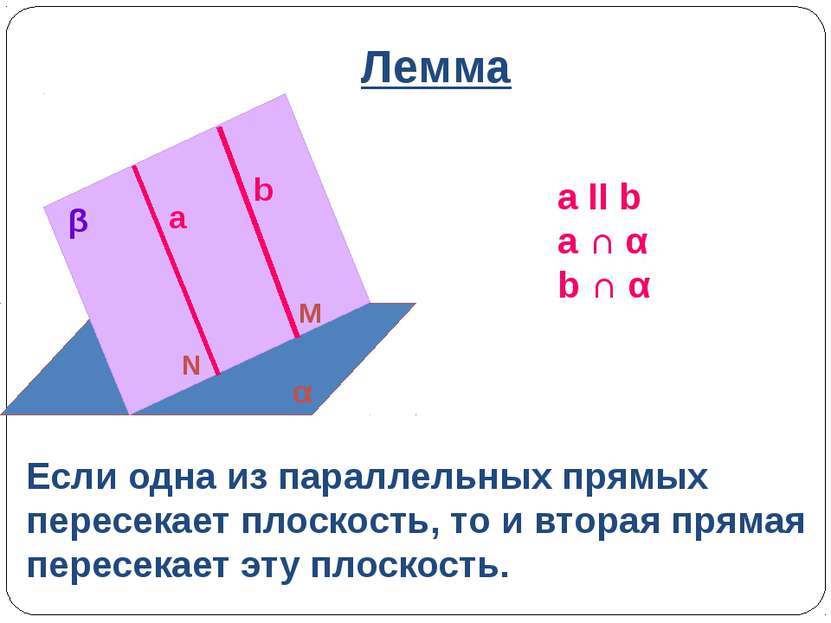
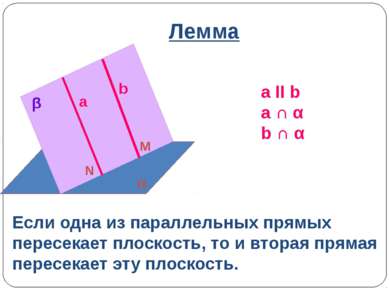 Лемма a ΙΙ b a ∩ α b ∩ α Если одна из параллельных прямых пересекает плоскость, то и вторая прямая пересекает эту плоскость. a b α β M N
Лемма a ΙΙ b a ∩ α b ∩ α Если одна из параллельных прямых пересекает плоскость, то и вторая прямая пересекает эту плоскость. a b α β M N
Cлайд 5
 ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Если две прямые параллельны третьей прямой, то они параллельны между собой. a ΙΙ b a ΙΙ c b ΙΙ c
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Если две прямые параллельны третьей прямой, то они параллельны между собой. a ΙΙ b a ΙΙ c b ΙΙ c
Cлайд 6
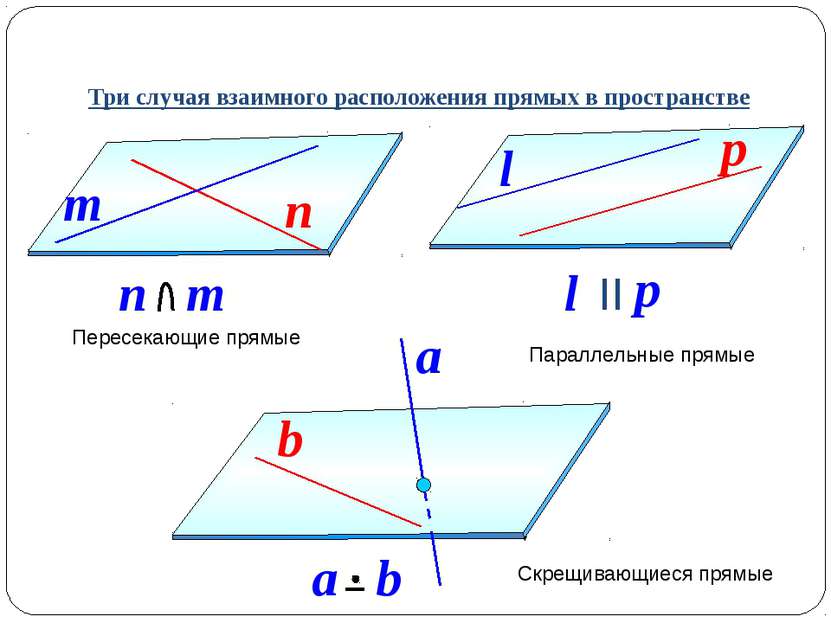
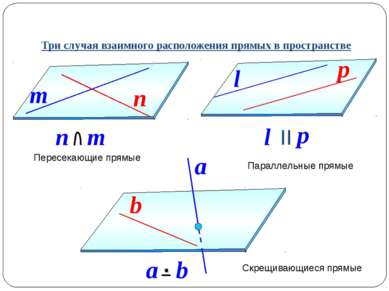 Три случая взаимного расположения прямых в пространстве Пересекающие прямые Параллельные прямые Скрещивающиеся прямые n m n m p l l p II a a b
Три случая взаимного расположения прямых в пространстве Пересекающие прямые Параллельные прямые Скрещивающиеся прямые n m n m p l l p II a a b
Cлайд 7
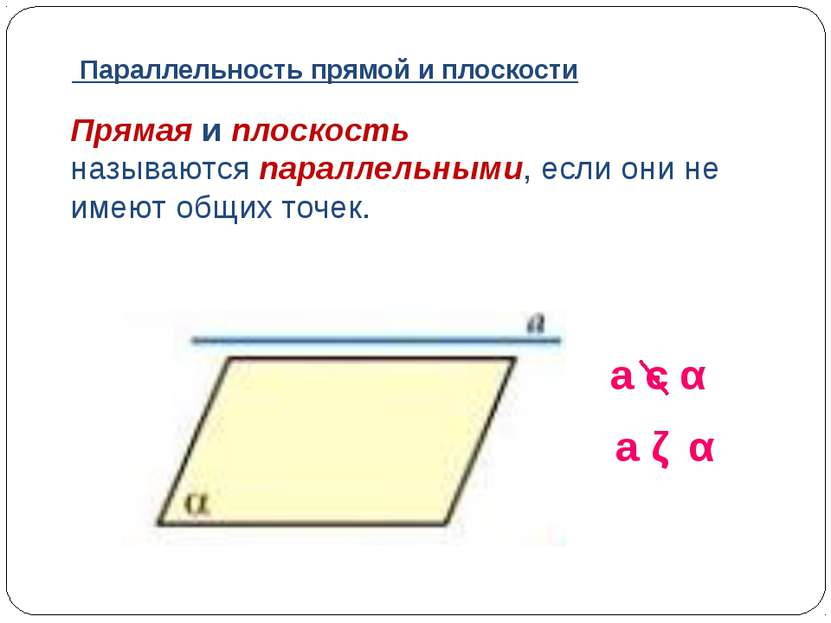
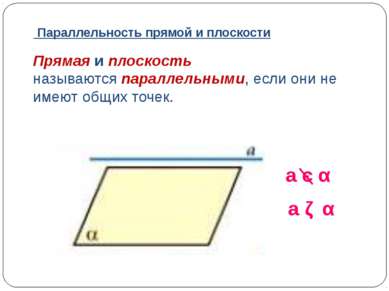 Прямая и плоскость называются параллельными, если они не имеют общих точек. a є α a ǁ α Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек. a є α a ǁ α Параллельность прямой и плоскости
Cлайд 8
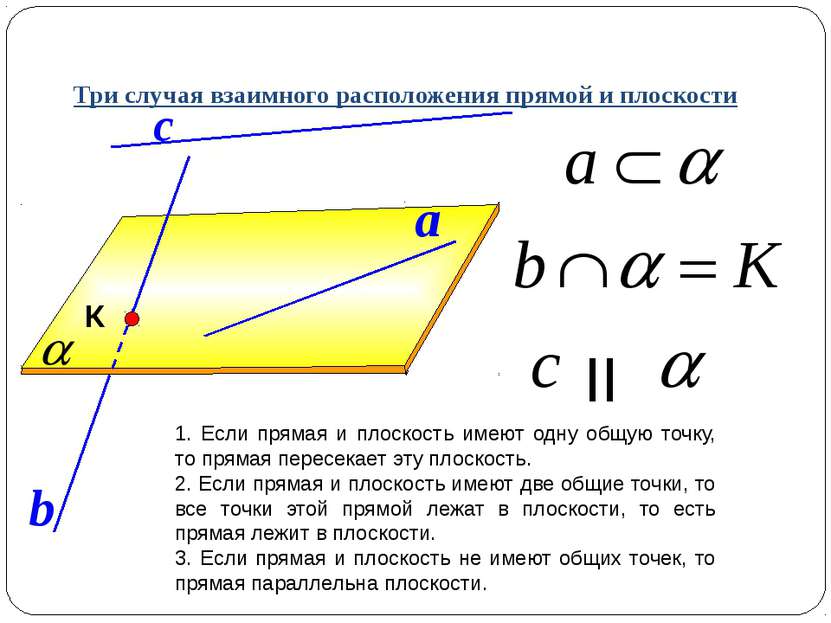
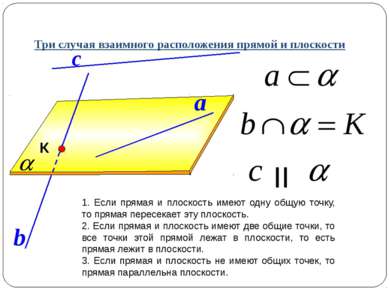 Три случая взаимного расположения прямой и плоскости 1. Если прямая и плоскость имеют одну общую точку, то прямая пересекает эту плоскость. 2. Если прямая и плоскость имеют две общие точки, то все точки этой прямой лежат в плоскости, то есть прямая лежит в плоскости. 3. Если прямая и плоскость не имеют общих точек, то прямая параллельна плоскости. b К a с II
Три случая взаимного расположения прямой и плоскости 1. Если прямая и плоскость имеют одну общую точку, то прямая пересекает эту плоскость. 2. Если прямая и плоскость имеют две общие точки, то все точки этой прямой лежат в плоскости, то есть прямая лежит в плоскости. 3. Если прямая и плоскость не имеют общих точек, то прямая параллельна плоскости. b К a с II
Cлайд 9
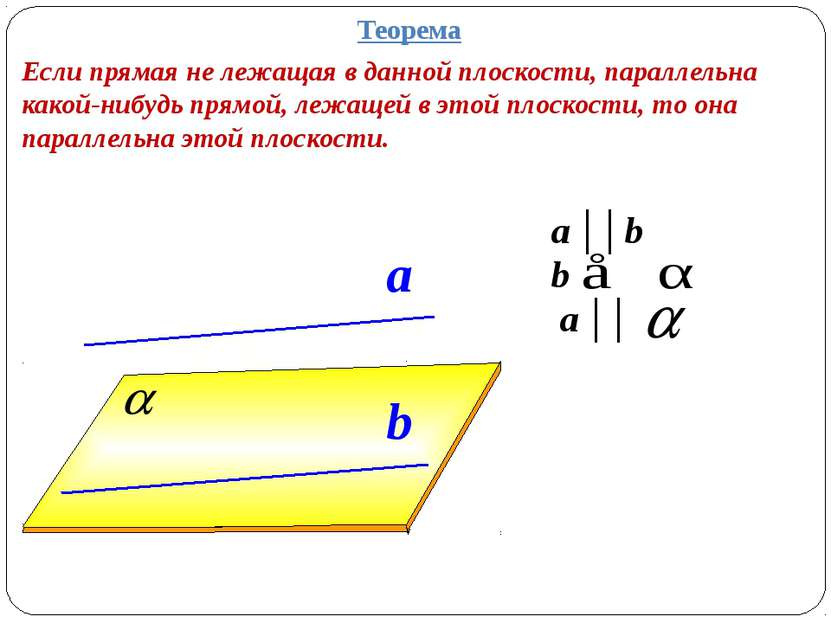
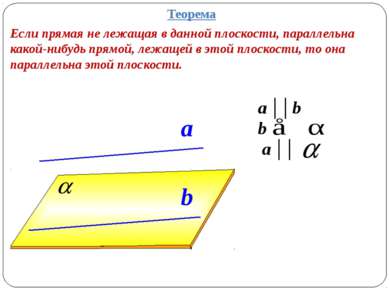 a ││b b a ││ a b Теорема Если прямая не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
a ││b b a ││ a b Теорема Если прямая не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
Cлайд 10
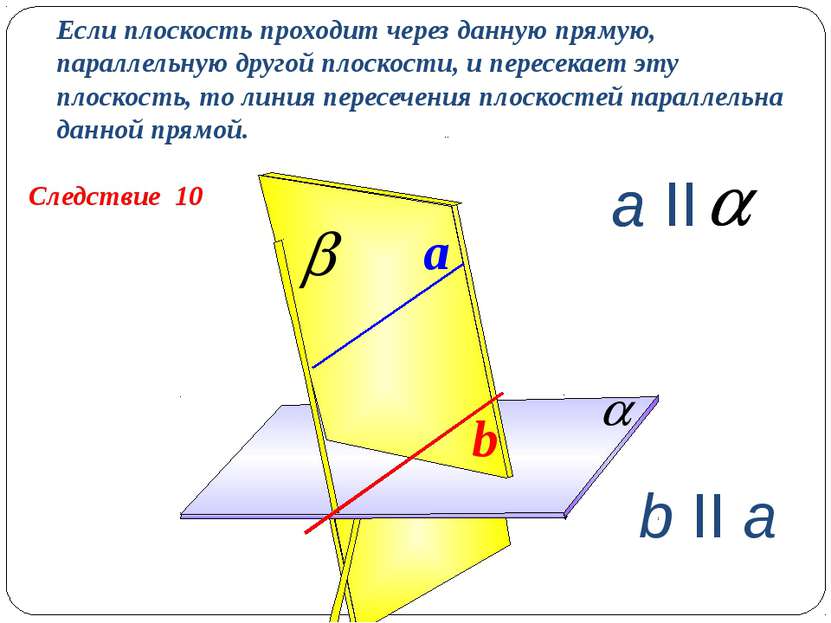
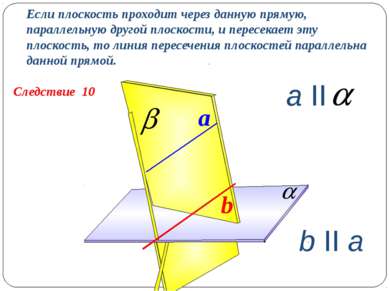 Следствие 10 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. a b II a b a II a II
Следствие 10 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. a b II a b a II a II
Cлайд 11
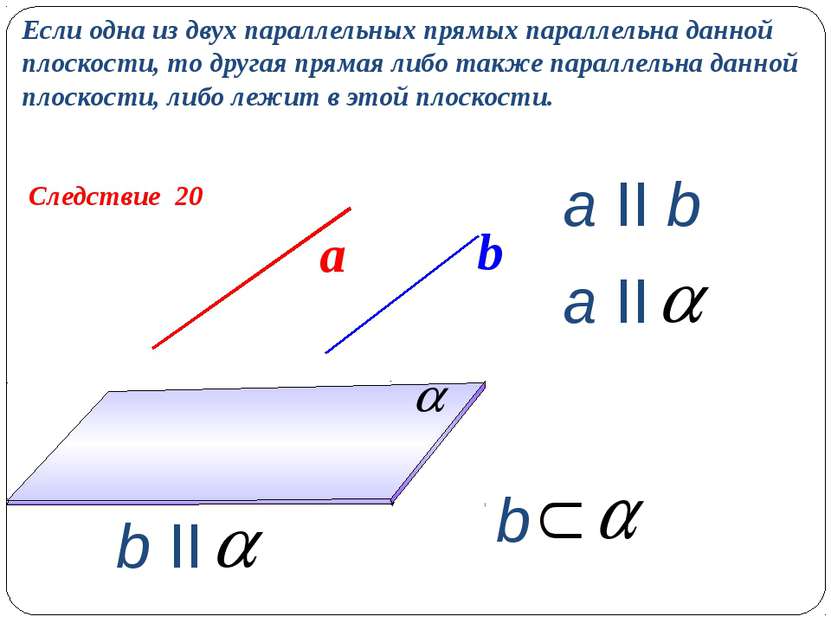
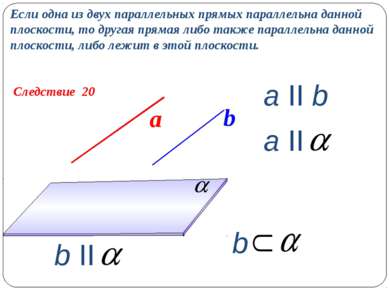 Следствие 20 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. a II b а b a II b II b
Следствие 20 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. a II b а b a II b II b
Cлайд 12
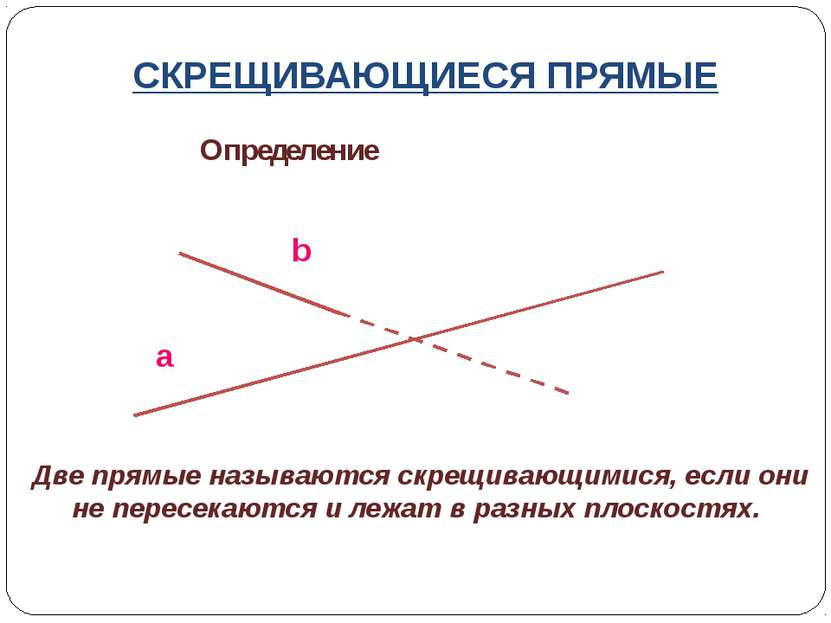
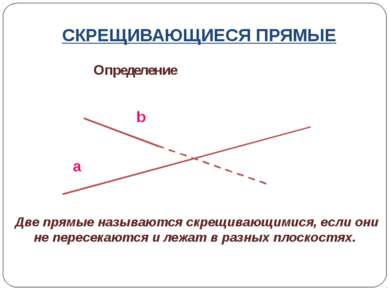 СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Определение a b Две прямые называются скрещивающимися, если они не пересекаются и лежат в разных плоскостях.
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Определение a b Две прямые называются скрещивающимися, если они не пересекаются и лежат в разных плоскостях.
Cлайд 13
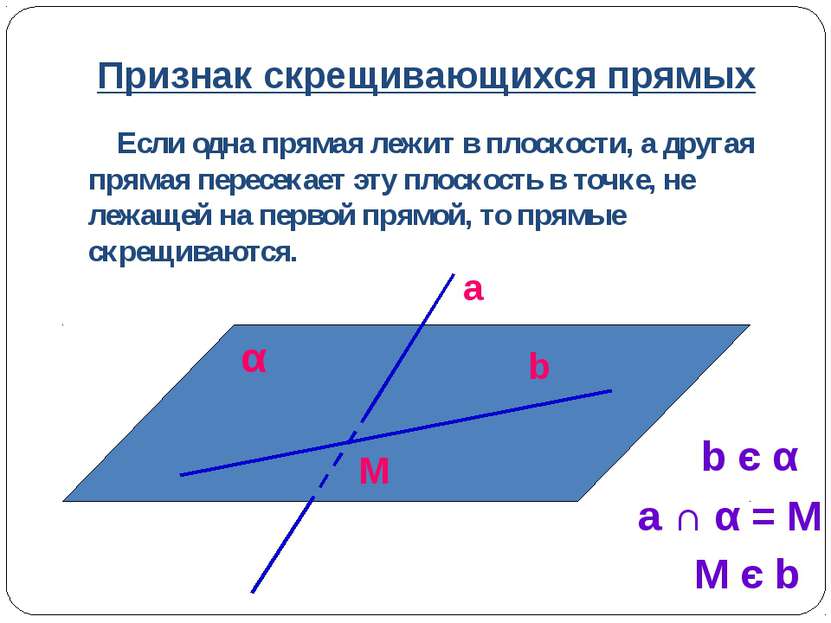
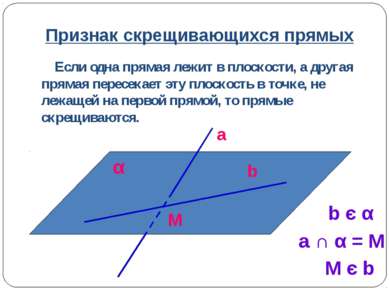 Признак скрещивающихся прямых Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещиваются. b є α a ∩ α = M M є b a b α M
Признак скрещивающихся прямых Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещиваются. b є α a ∩ α = M M є b a b α M
Cлайд 14
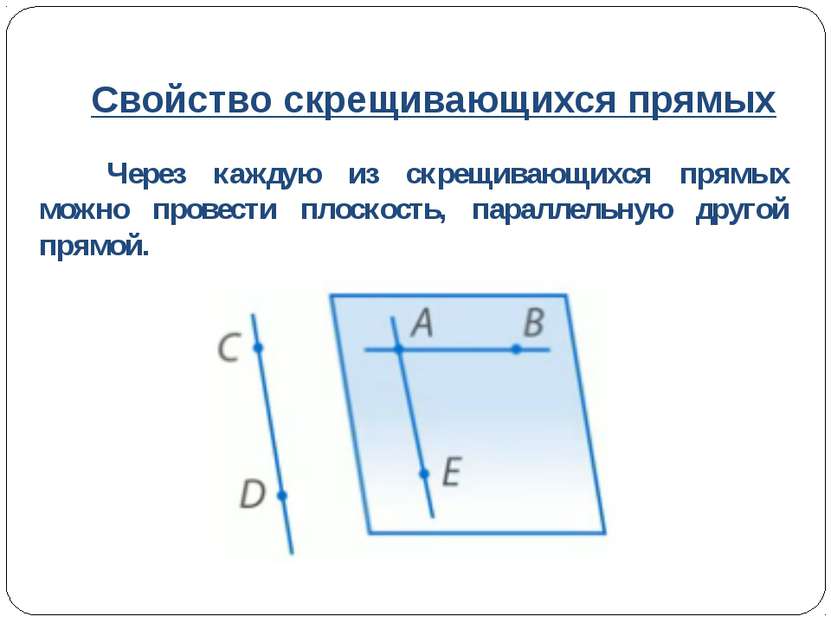
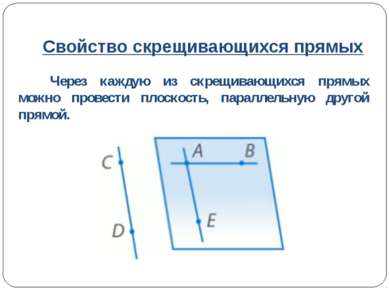 Свойство скрещивающихся прямых Через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
Свойство скрещивающихся прямых Через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
Cлайд 15
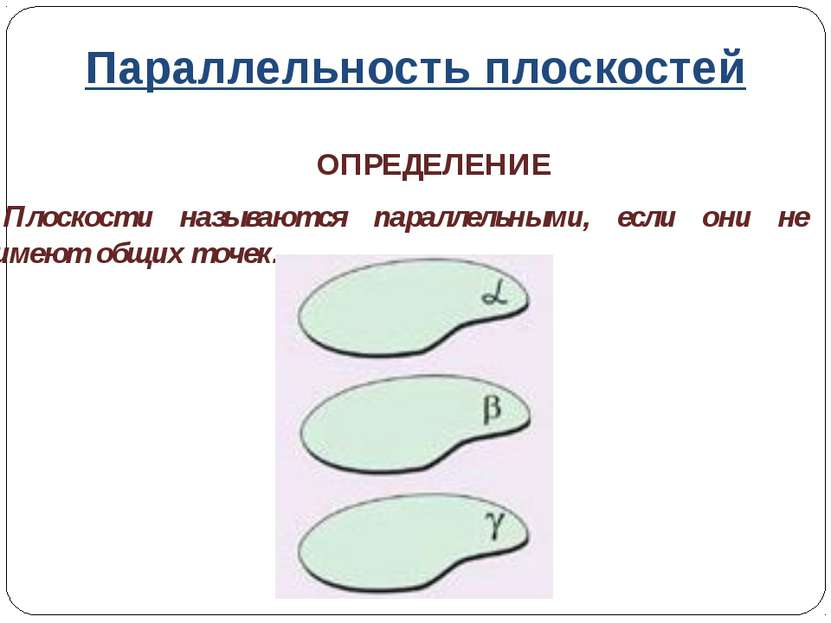
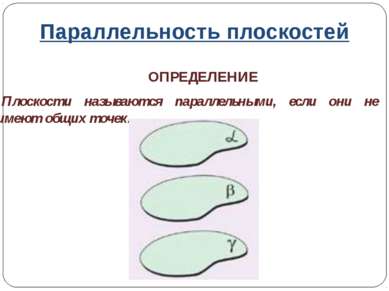 Параллельность плоскостей ОПРЕДЕЛЕНИЕ Плоскости называются параллельными, если они не имеют общих точек.
Параллельность плоскостей ОПРЕДЕЛЕНИЕ Плоскости называются параллельными, если они не имеют общих точек.
Cлайд 16
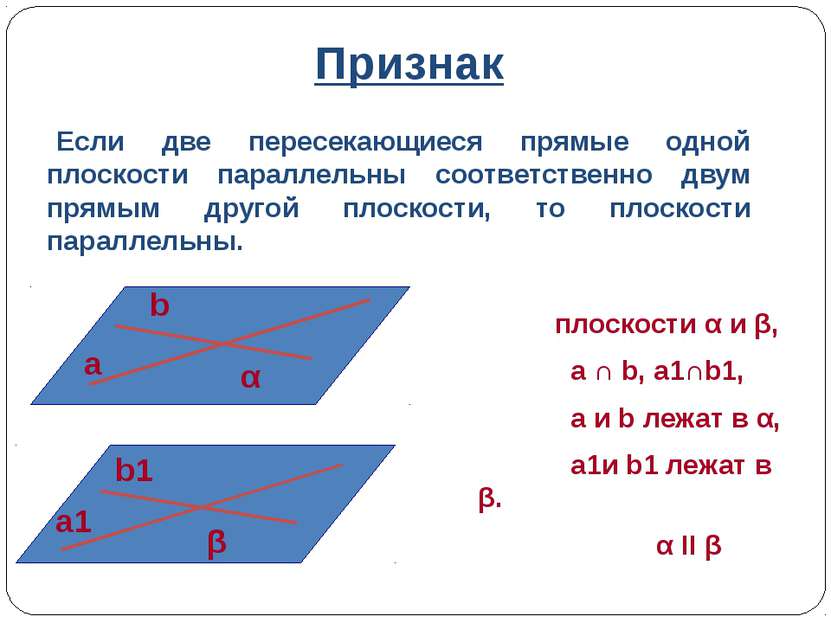
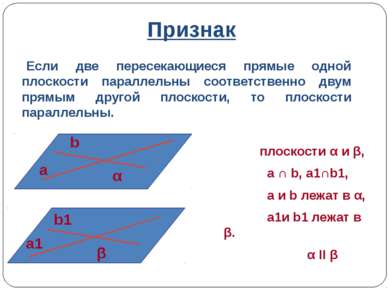 Признак плоскости α и β, a ∩ b, a1∩b1, a и b лежат в α, a1и b1 лежат в β. α II β Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны. a b α b1 a1 β
Признак плоскости α и β, a ∩ b, a1∩b1, a и b лежат в α, a1и b1 лежат в β. α II β Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны. a b α b1 a1 β
Cлайд 17
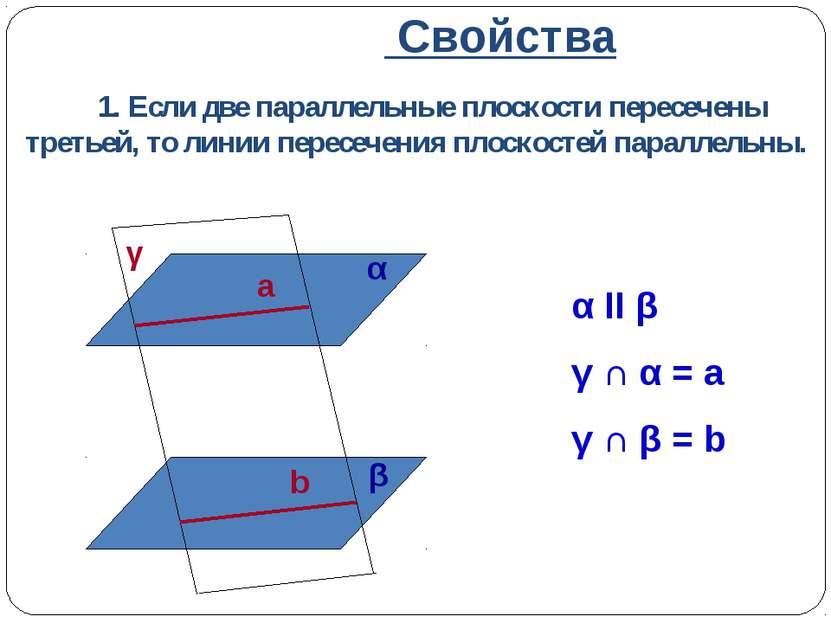
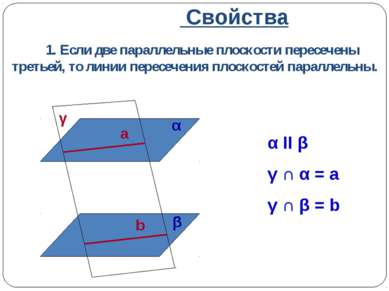 Свойства 1. Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны. α II β γ ∩ α = a γ ∩ β = b α β γ a b
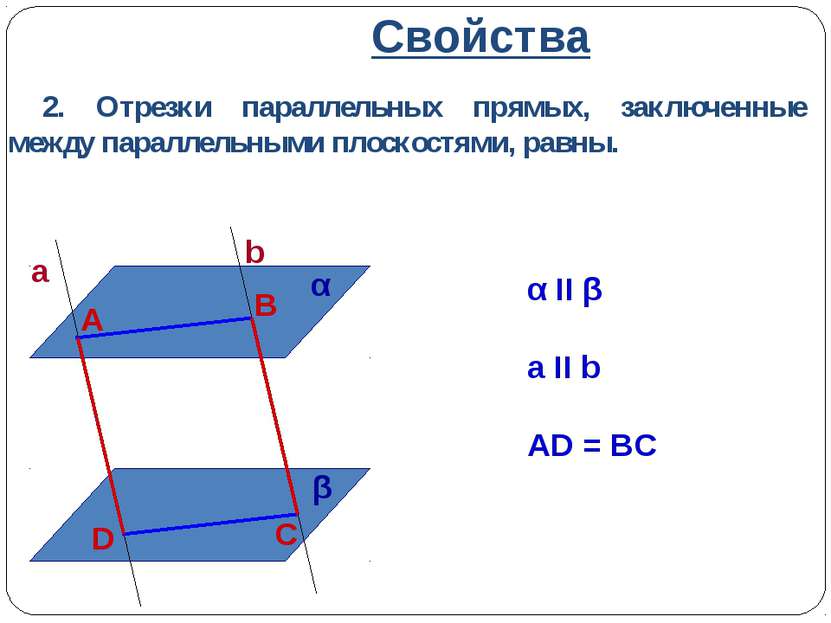
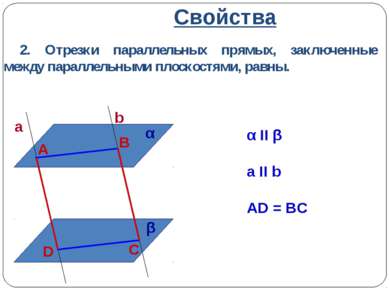
Свойства 1. Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны. α II β γ ∩ α = a γ ∩ β = b α β γ a b