X
Код презентации скопируйте его
Средняя линия трапеции
Скачать эту презентациюПрезентация на тему Средняя линия трапеции
Скачать эту презентациюCлайд 1
 Работа по теме « Средняя линия трапеции» Ученика 9-2 класса Школы №593 Андреева Георгия Преподаватель : Петрова Наталья Васильевна
Работа по теме « Средняя линия трапеции» Ученика 9-2 класса Школы №593 Андреева Георгия Преподаватель : Петрова Наталья Васильевна
Cлайд 2
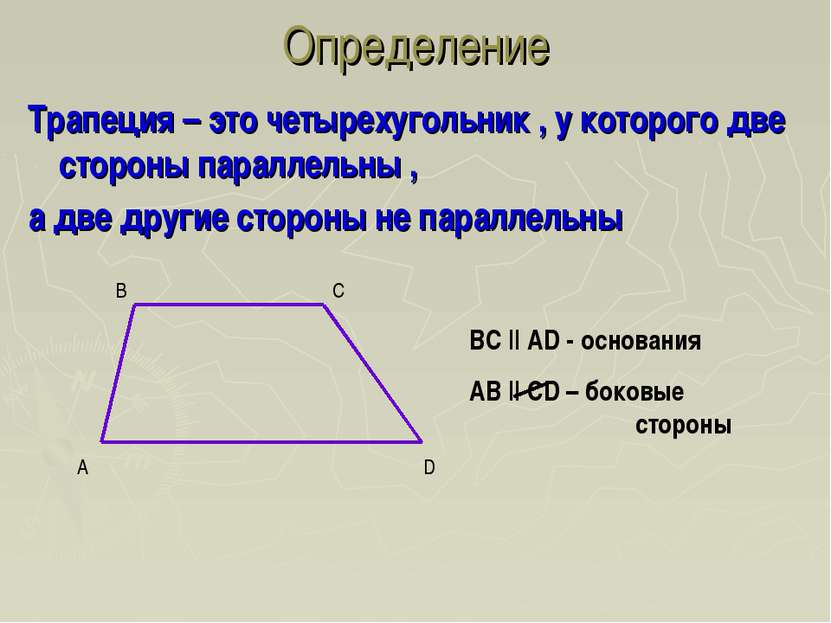
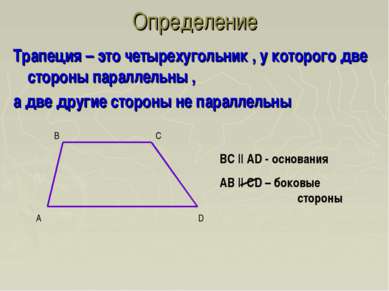 Трапеция – это четырехугольник , у которого две стороны параллельны , а две другие стороны не параллельны Определение
Трапеция – это четырехугольник , у которого две стороны параллельны , а две другие стороны не параллельны Определение
Cлайд 3
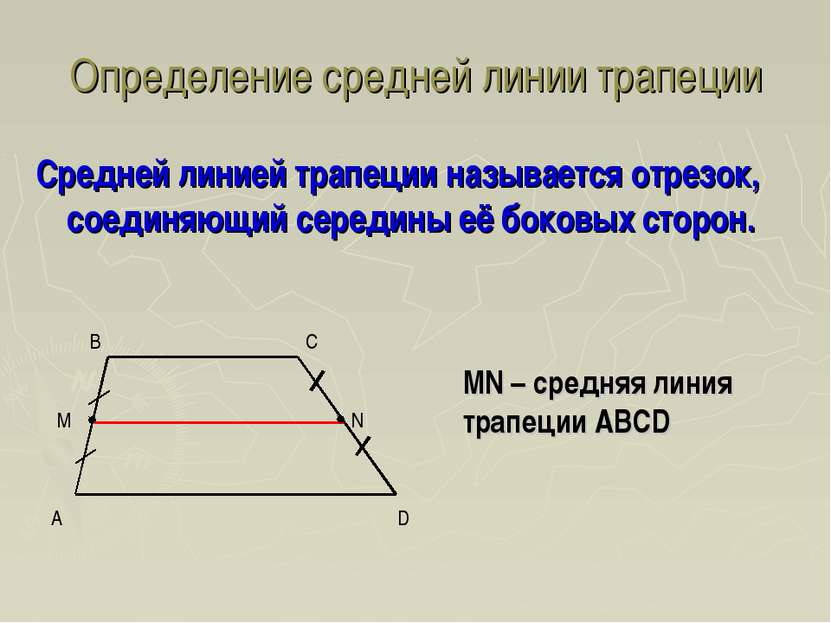
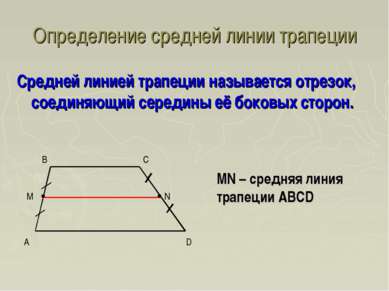 Определение средней линии трапеции Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. MN – средняя линия трапеции ABCD
Определение средней линии трапеции Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. MN – средняя линия трапеции ABCD
Cлайд 4
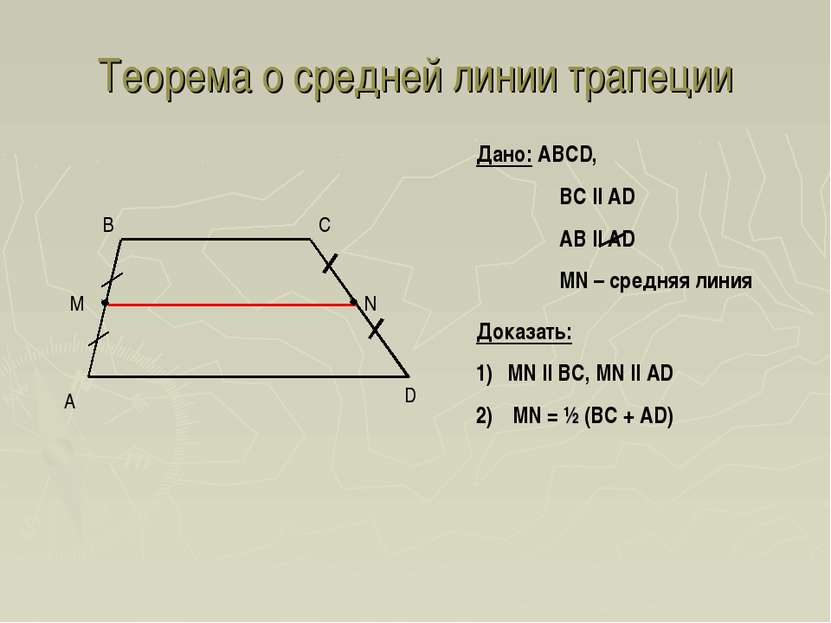
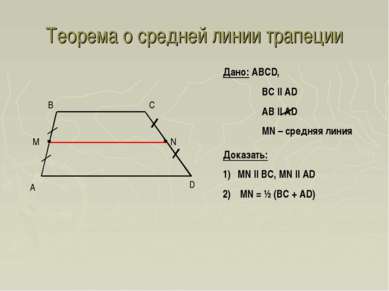 Теорема о средней линии трапеции A D B C Дано: ABCD, BC || AD AB || AD MN – средняя линия Доказать: MN || BC, MN || AD MN = ½ (BC + AD)
Теорема о средней линии трапеции A D B C Дано: ABCD, BC || AD AB || AD MN – средняя линия Доказать: MN || BC, MN || AD MN = ½ (BC + AD)
Cлайд 5
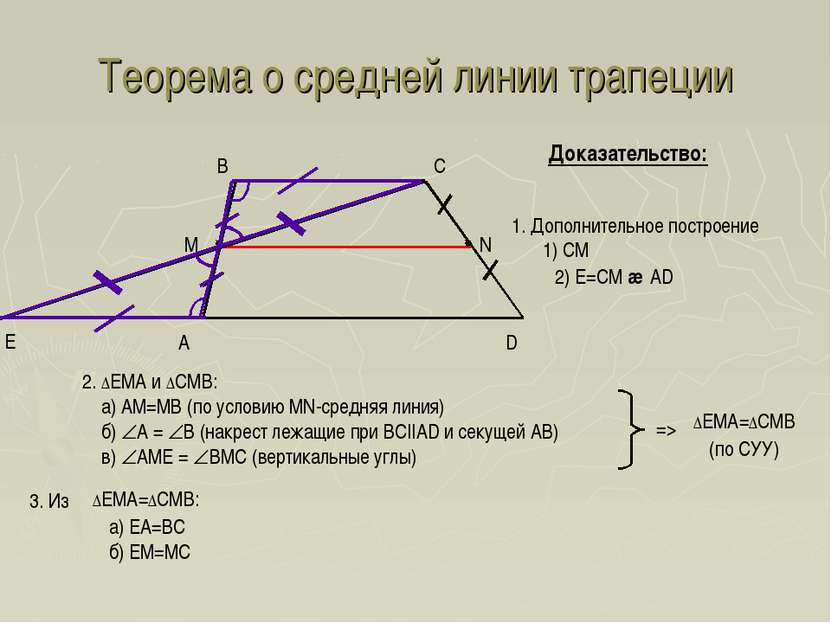
 Теорема о средней линии трапеции A D B C Доказательство: Е 1. Дополнительное построение 1) CM 2. ΔEMA и ΔCMB: а) AM=MB (по условию MN-средняя линия) б) A = B (накрест лежащие при BC||AD и секущей AB) в) AME = BMC (вертикальные углы) 2) E=CM ∩ AD а) EA=BC б) EM=MC
Теорема о средней линии трапеции A D B C Доказательство: Е 1. Дополнительное построение 1) CM 2. ΔEMA и ΔCMB: а) AM=MB (по условию MN-средняя линия) б) A = B (накрест лежащие при BC||AD и секущей AB) в) AME = BMC (вертикальные углы) 2) E=CM ∩ AD а) EA=BC б) EM=MC
Cлайд 6
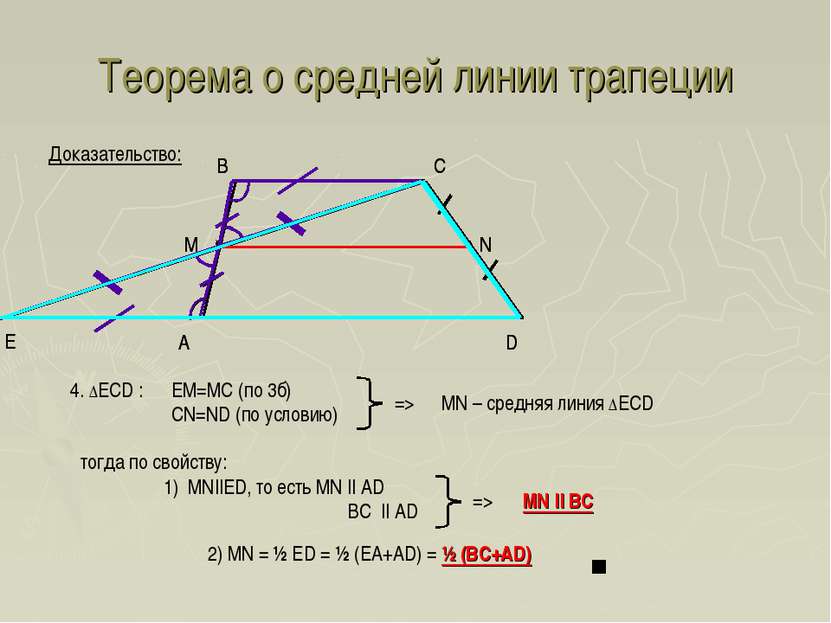
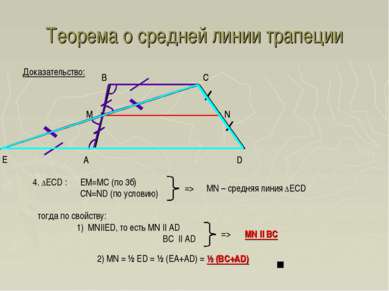 Теорема о средней линии трапеции A D B C Доказательство: Е 4. ΔECD : EM=MC (по 3б) CN=ND (по условию) тогда по свойству: 1) MN||ED, то есть MN || AD BC || AD 2) MN = ½ ED = ½ (EA+AD) = ½ (BC+AD) A D B C Е
Теорема о средней линии трапеции A D B C Доказательство: Е 4. ΔECD : EM=MC (по 3б) CN=ND (по условию) тогда по свойству: 1) MN||ED, то есть MN || AD BC || AD 2) MN = ½ ED = ½ (EA+AD) = ½ (BC+AD) A D B C Е
Cлайд 10
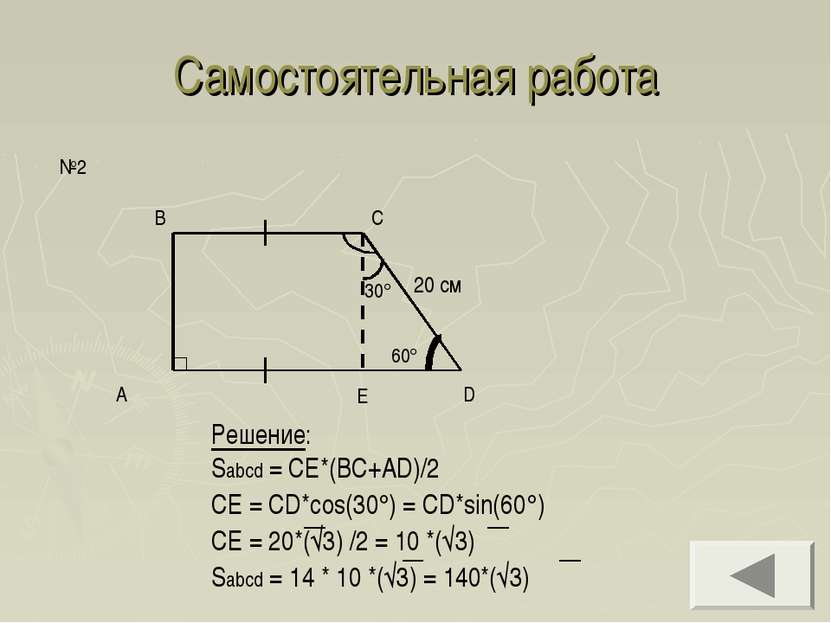
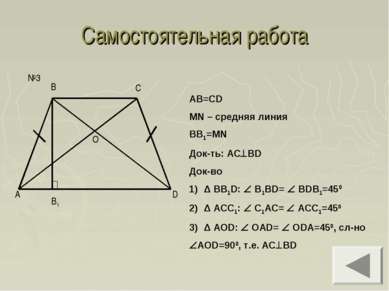
 Самостоятельная работа 5 см №1 Решение: BC = Х см AD = 1.5X см BC+AD = 10 см X + 1.5X = 10 X = 4 BC = 4 см AD = 6 см
Самостоятельная работа 5 см №1 Решение: BC = Х см AD = 1.5X см BC+AD = 10 см X + 1.5X = 10 X = 4 BC = 4 см AD = 6 см