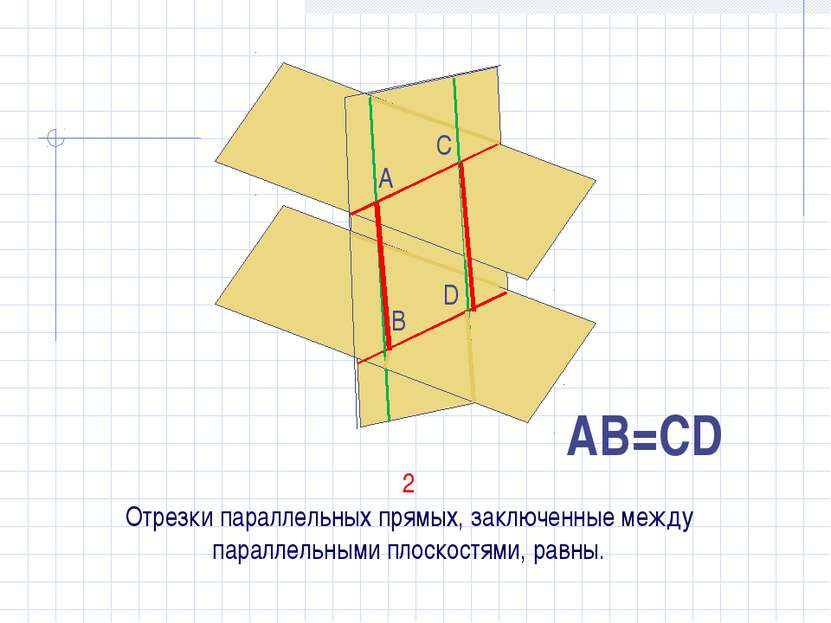
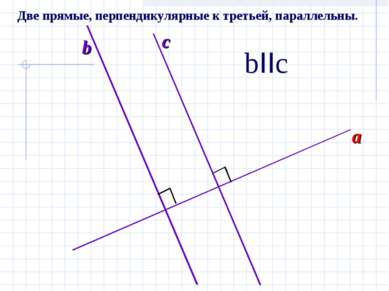
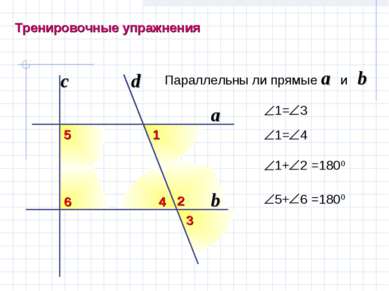
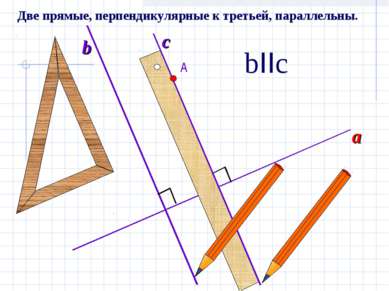
X
Код презентации скопируйте его
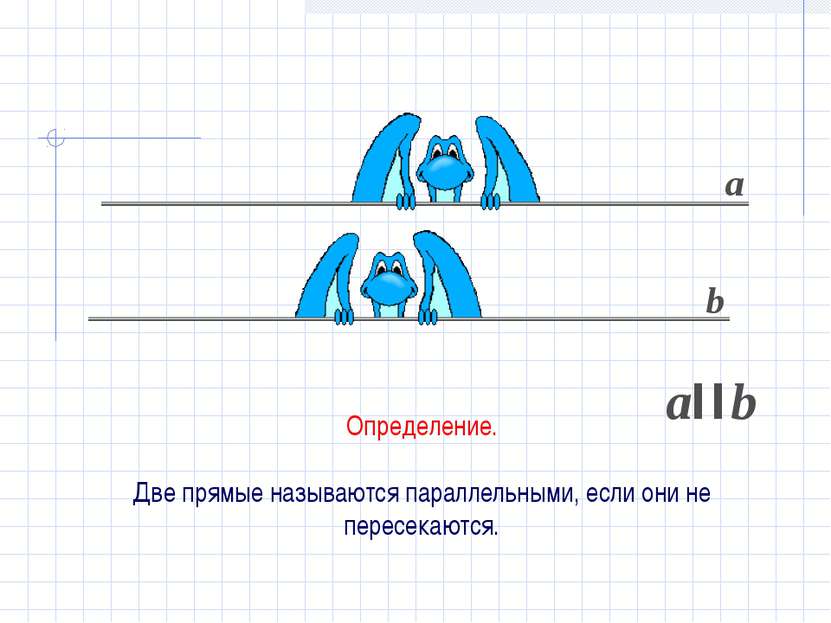
Параллельность
Скачать эту презентацию
Презентация на тему Параллельность
Скачать эту презентациюCлайд 1
Cлайд 2
Cлайд 3
Определение. Две прямые называются параллельными, если они не пересекаются. а b аIIb
Cлайд 4
Cлайд 5
a b c bIIc Две прямые, перпендикулярные к третьей, параллельны.
Cлайд 6
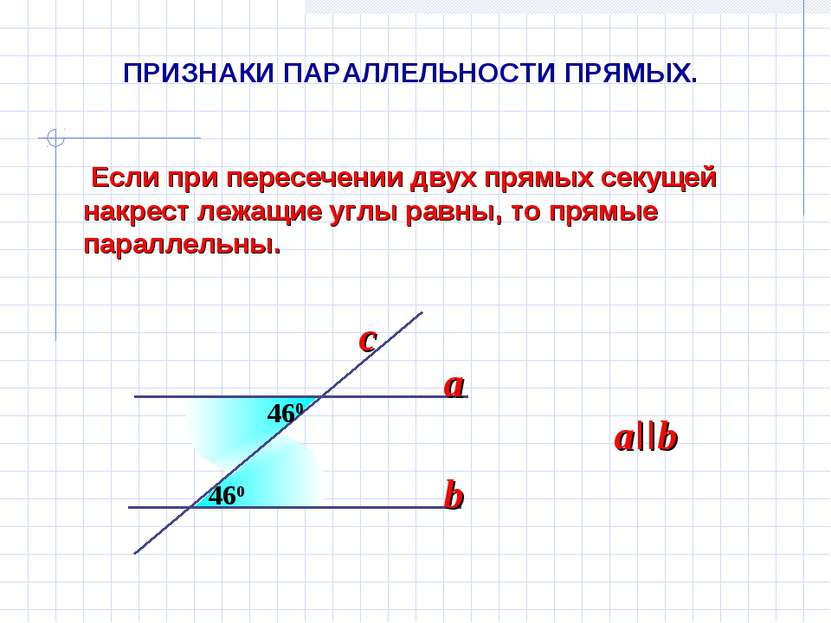
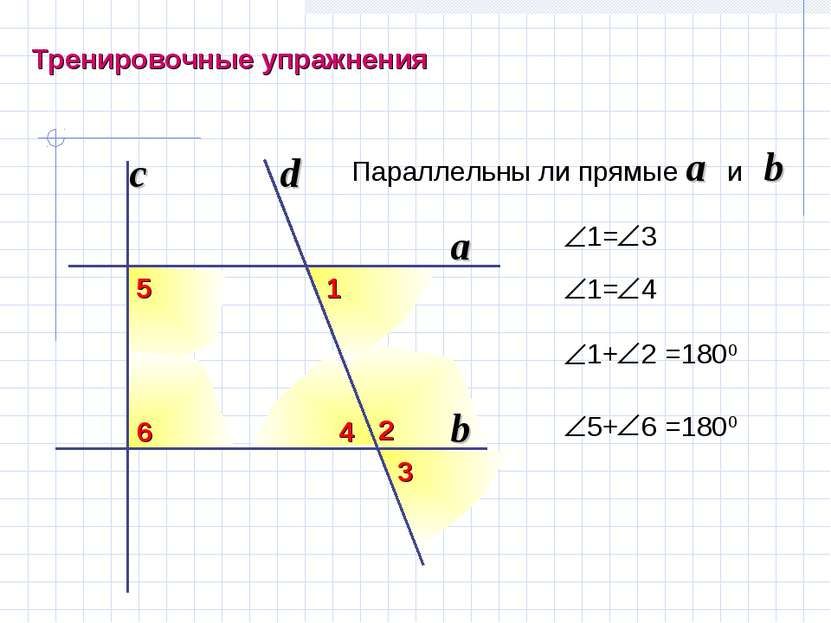
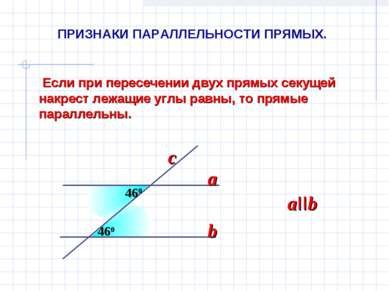Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 460 460 a b aIIb c ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.
Cлайд 7
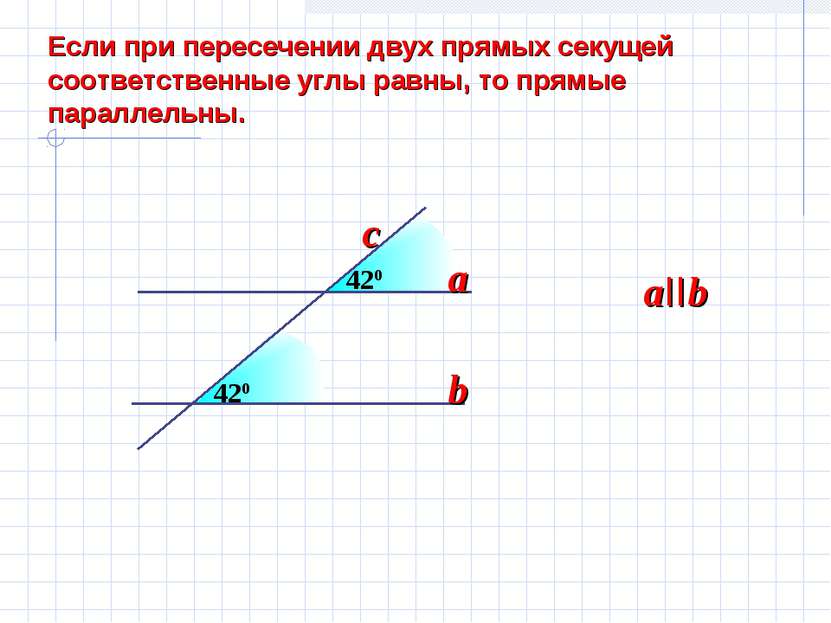
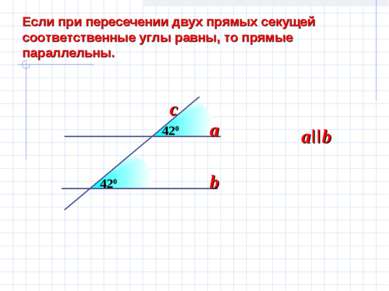420 Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 420 a b aIIb c
Cлайд 8
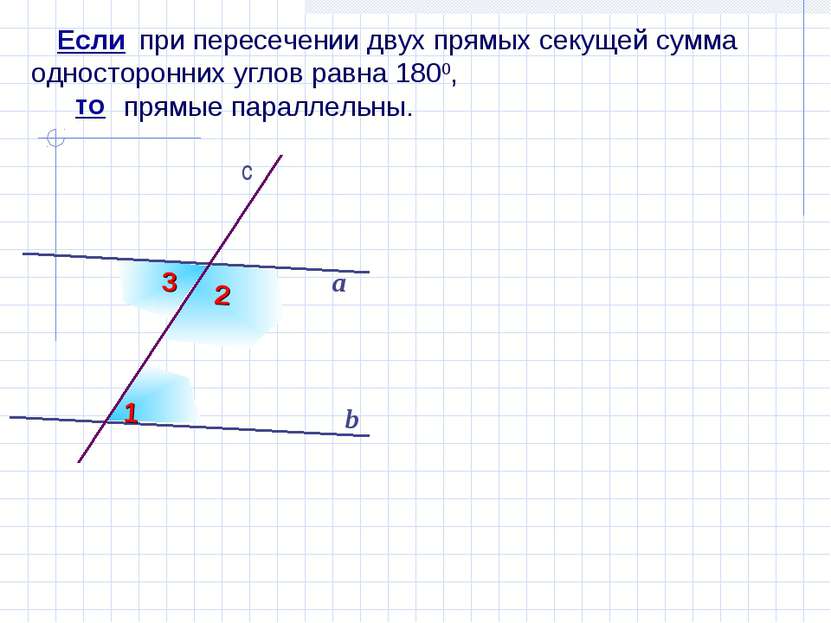
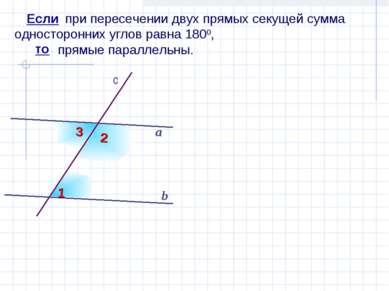при пересечении двух прямых секущей сумма односторонних углов равна 1800, прямые параллельны. b а Если то 1 2 c
Cлайд 9
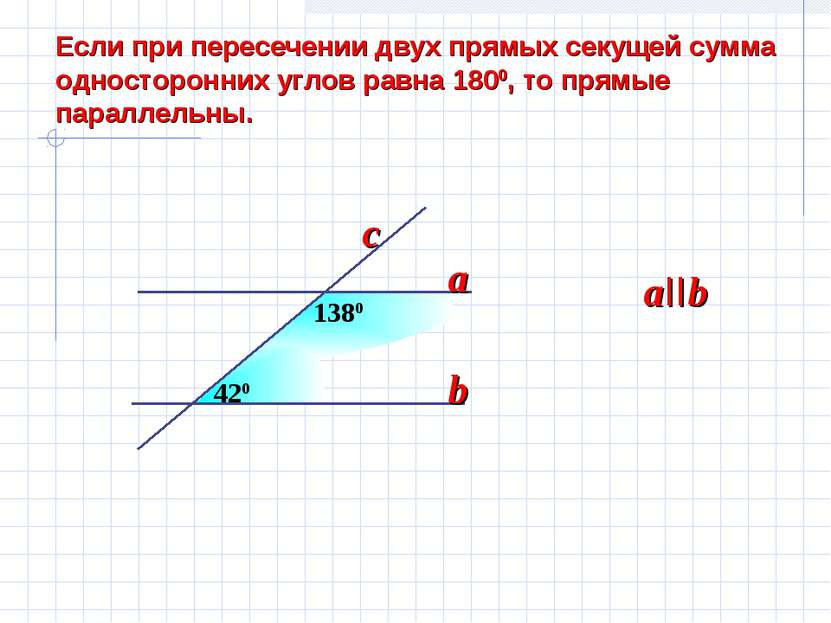
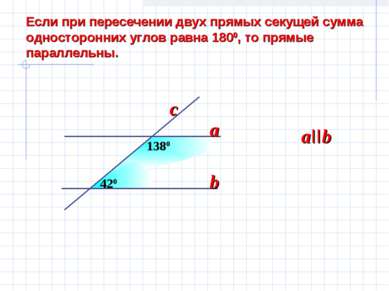Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны. 420 1380 a b aIIb c
Cлайд 10
Тренировочные упражнения Параллельны ли прямые a и b b a d c 1 3 2 4 6 5
Cлайд 11
А a b c bIIc Две прямые, перпендикулярные к третьей, параллельны.
Cлайд 12
b bIIc Практические способы построения параллельных прямых
Cлайд 13
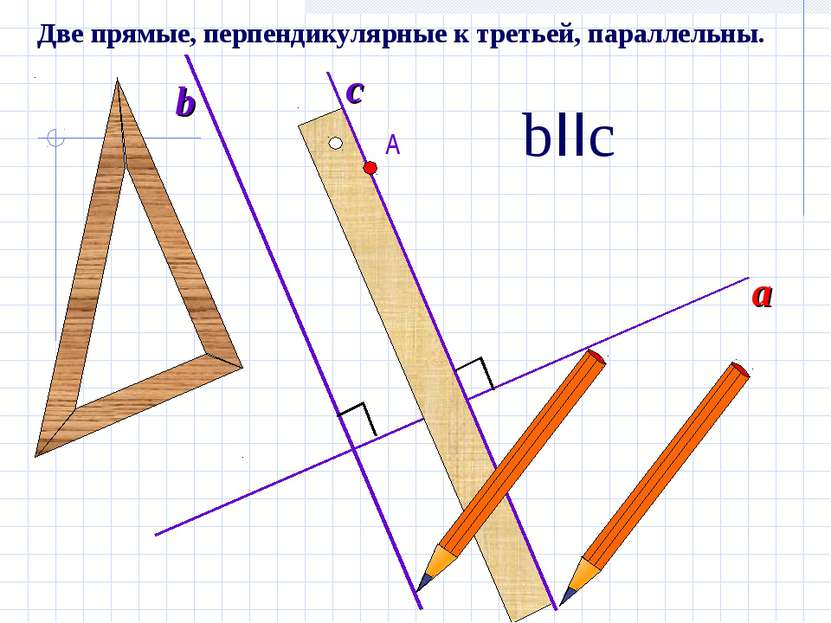
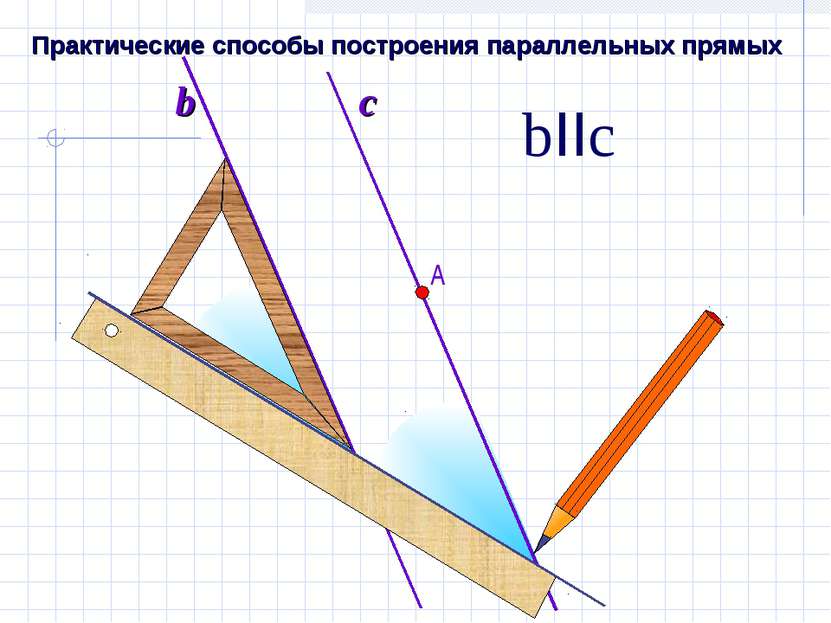
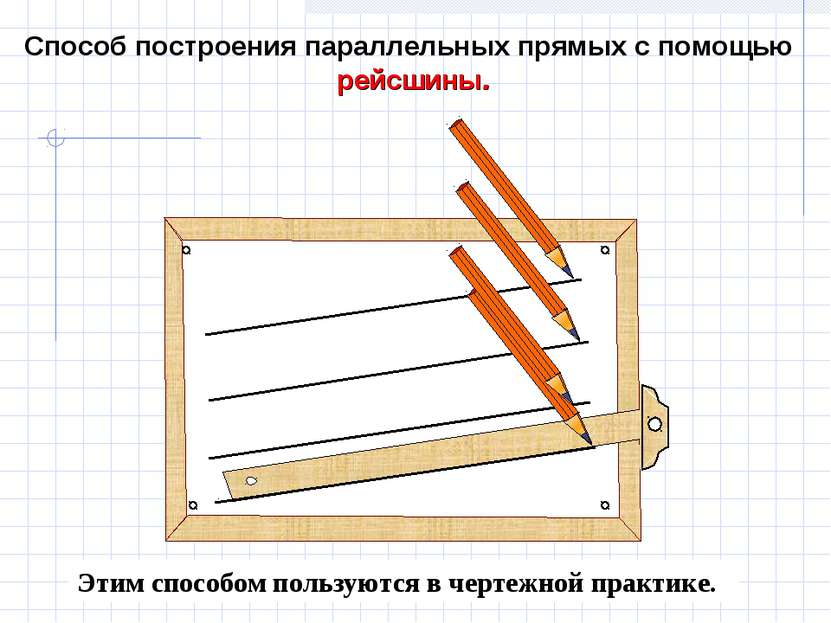
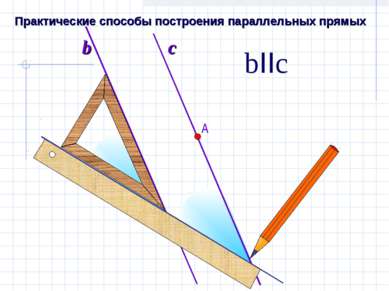
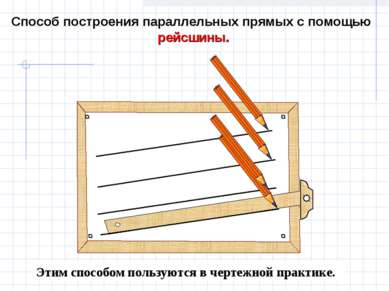Этим способом пользуются в чертежной практике. Способ построения параллельных прямых с помощью рейсшины.
Cлайд 14
Cлайд 15
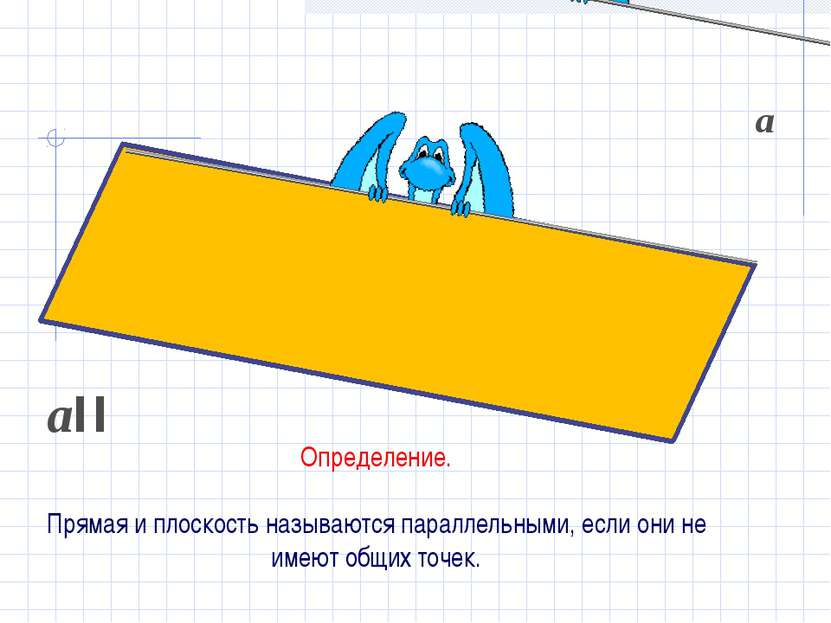
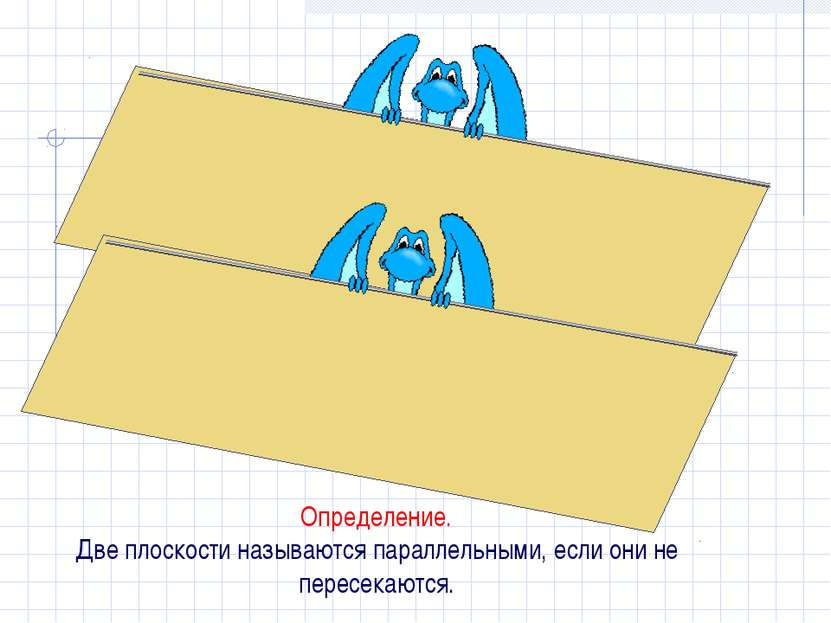
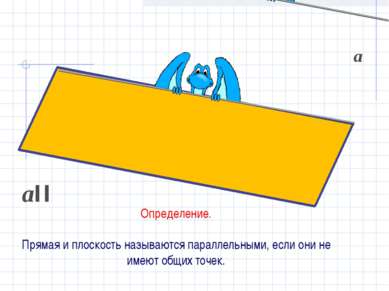Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек. аIIβ а β
Cлайд 16
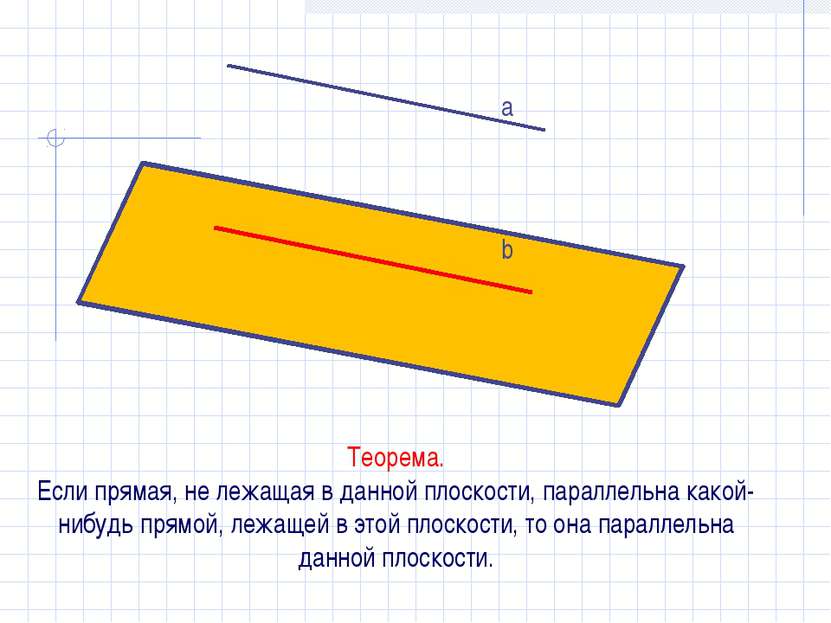
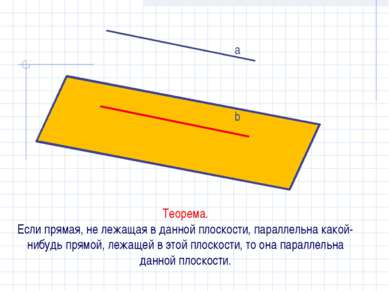Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. a b β
Cлайд 17
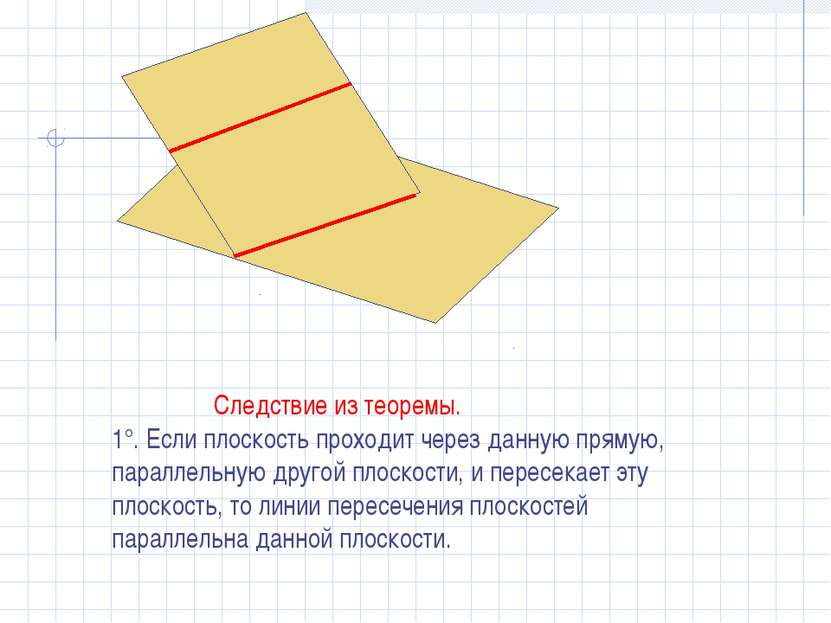
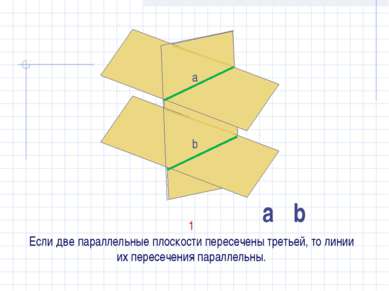
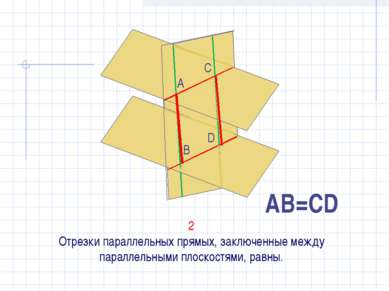
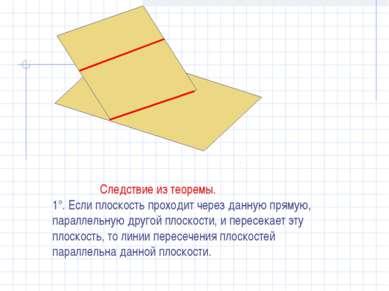Следствие из теоремы. 1°. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линии пересечения плоскостей параллельна данной плоскости. β
Cлайд 18
Следствие из теоремы. 2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Cлайд 19
Cлайд 20
β α Определение. Две плоскости называются параллельными, если они не пересекаются.
Cлайд 21
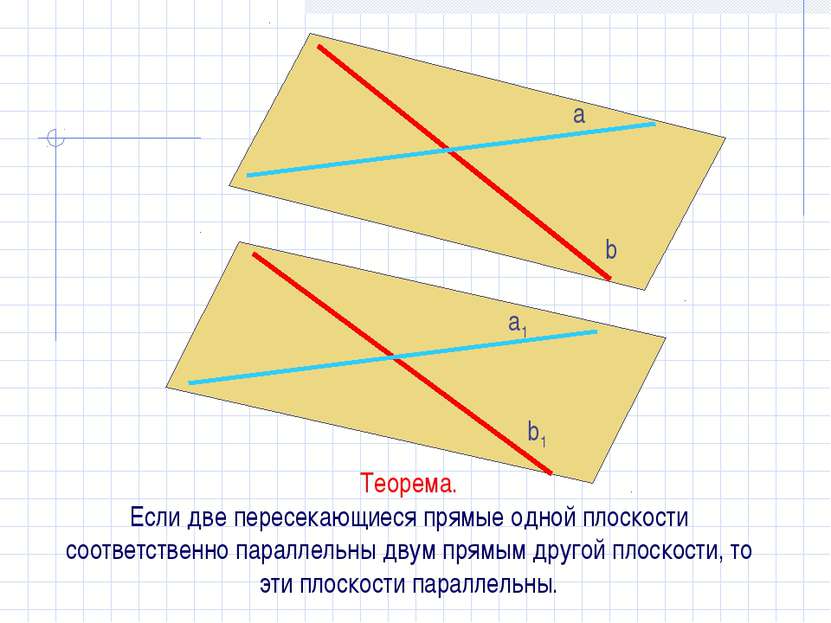
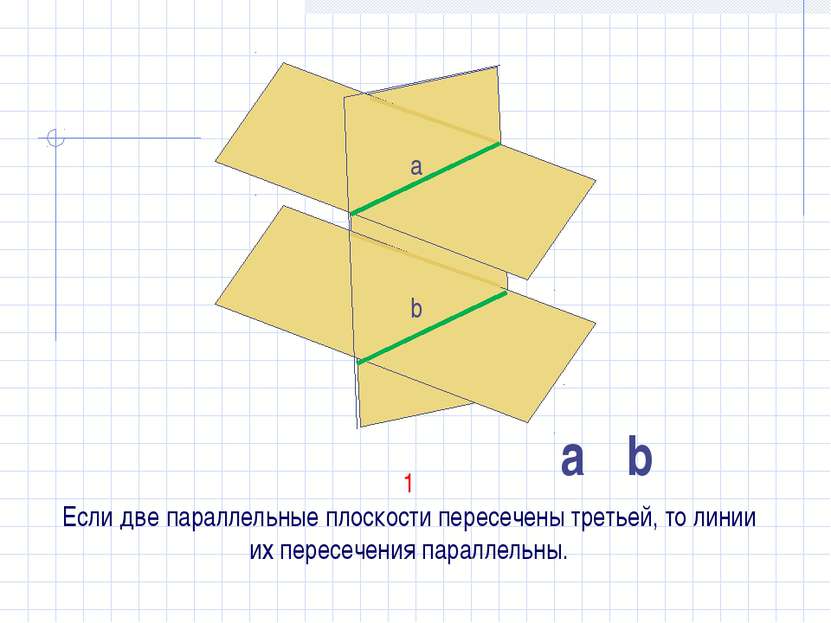
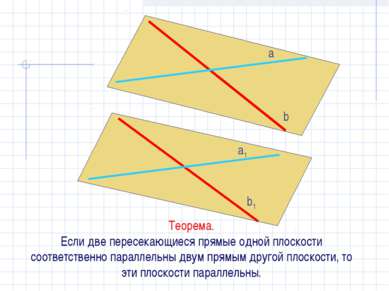Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. α β a b a1 b1 α׀׀β
Cлайд 22
Cлайд 23
1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. α β γ a b a׀׀b
Cлайд 24
2 Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. AB=CD
