X
Код презентации скопируйте его
Перпендикулярные прямые в пространстве
Скачать эту презентацию
Презентация на тему Перпендикулярные прямые в пространстве
Скачать эту презентациюCлайд 1
«Перпендикулярные прямые в пространстве» «Перпендикулярность прямой и плоскости» Тема урока: МОУ СОШ №256 г.Фокино
Cлайд 2
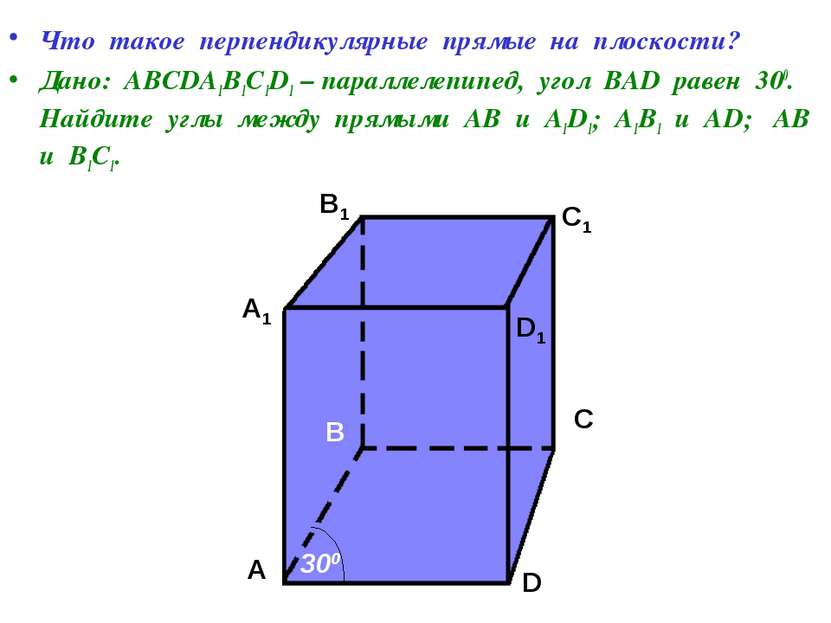
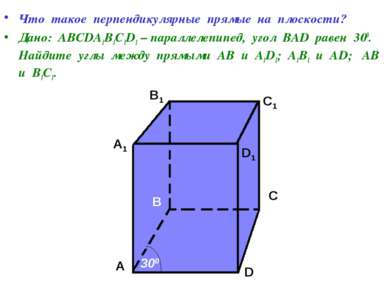Что такое перпендикулярные прямые на плоскости? Дано: АВСDA1B1C1D1 – параллелепипед, угол ВАD равен 300. Найдите углы между прямыми АВ и А1D1; А1В1 и АD; АВ и В1С1. А А1 В В1 С С1 D D1 300
Cлайд 3
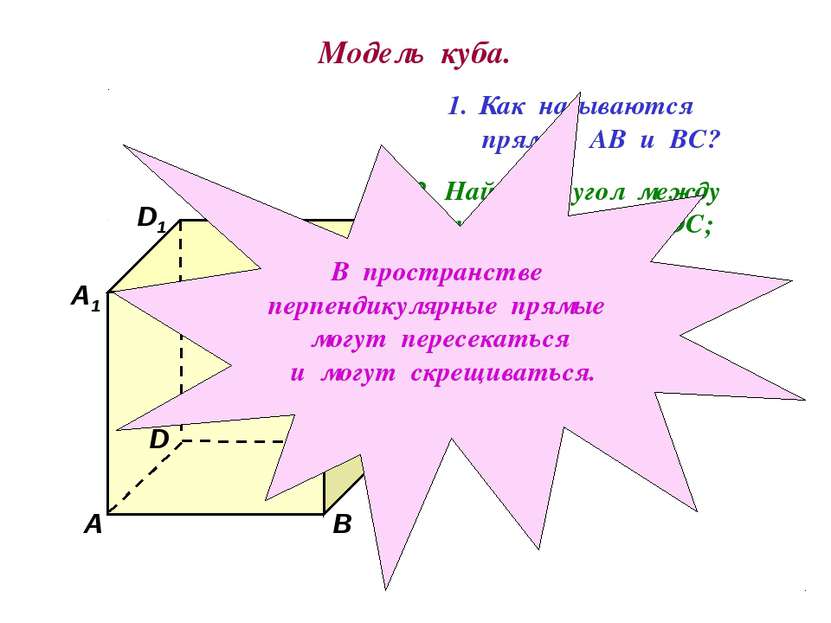
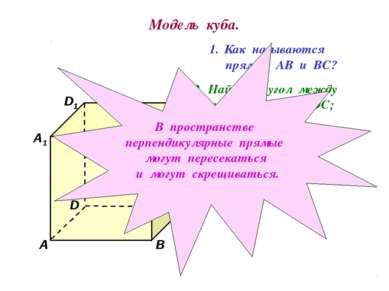Модель куба. D1 В А1 А D С1 С В1 Как называются прямые АВ и ВС? Найдите угол между прямыми АА1 и DC; ВВ1 и АD. В пространстве перпендикулярные прямые могут пересекаться и могут скрещиваться.
Cлайд 4
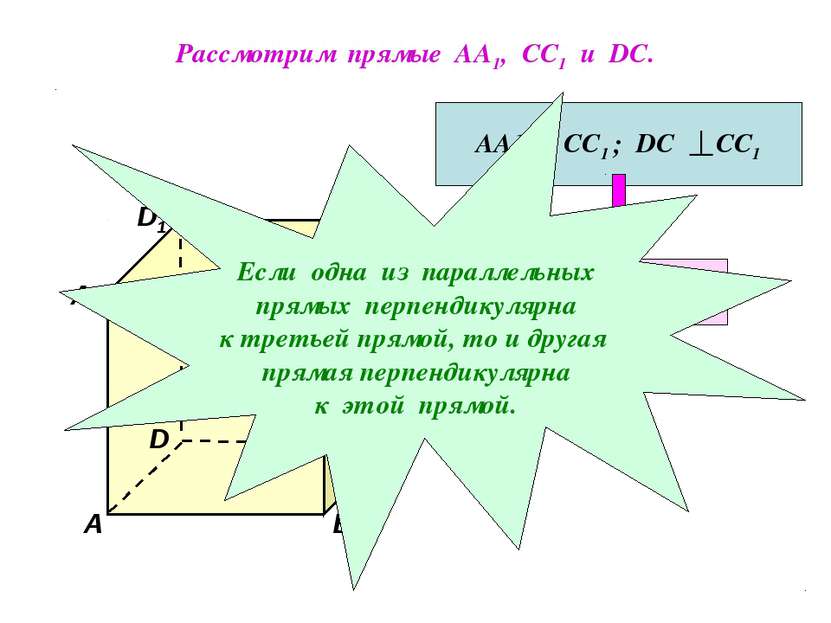
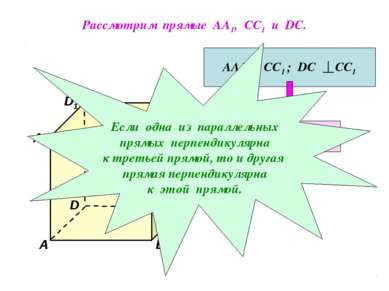Рассмотрим прямые АА1, СС1 и DC. D1 В А1 А D С1 С В1 АА1 СС1 ; DC СС1 АА1 DC Если одна из параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Cлайд 5
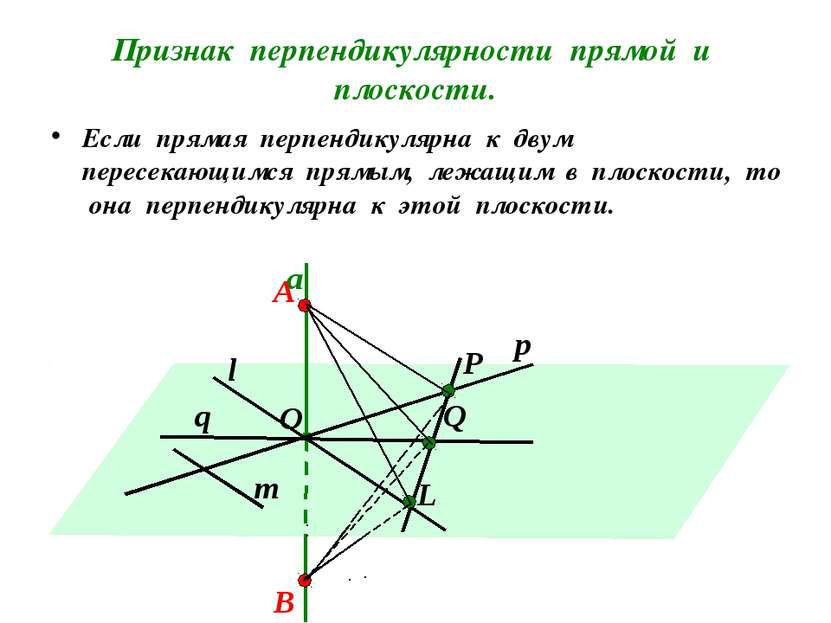
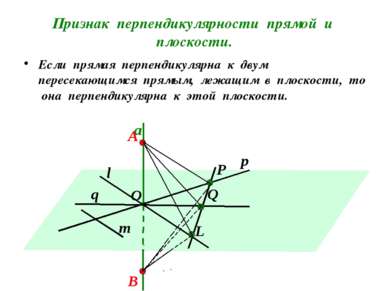
Найдите угол между прямой АА1 и прямыми плоскости (АВС): АВ, АD, АС, ВD, МN. D1 В А1 А D С1 С В1 N М 900 900 900 900 900 Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Cлайд 6
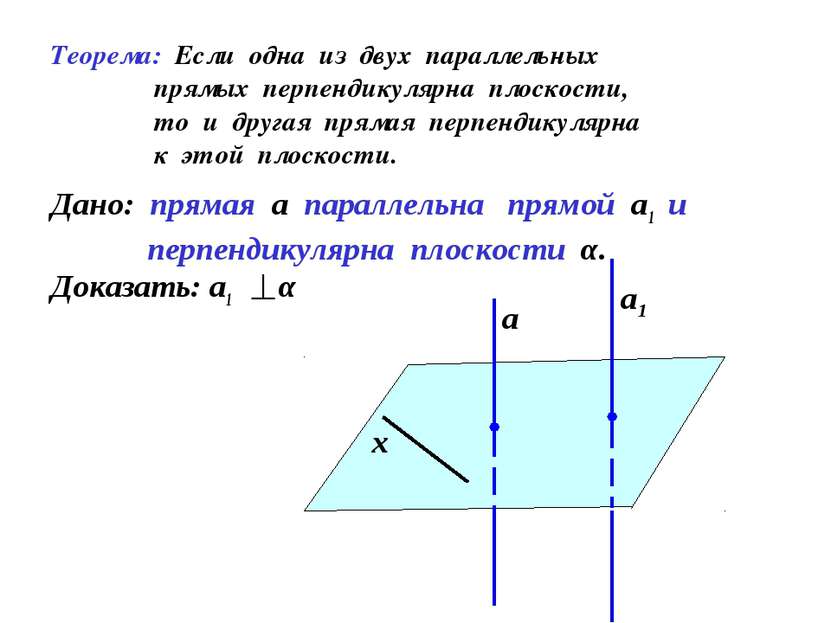
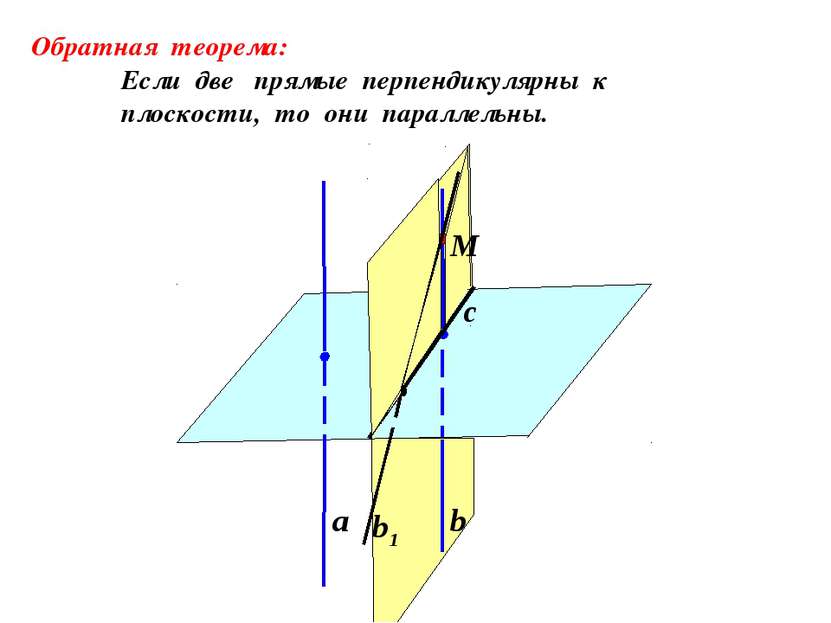
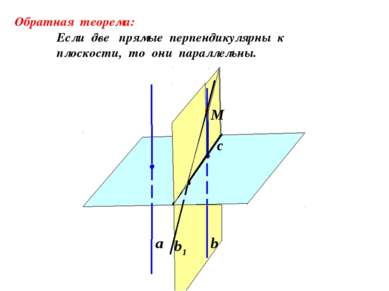
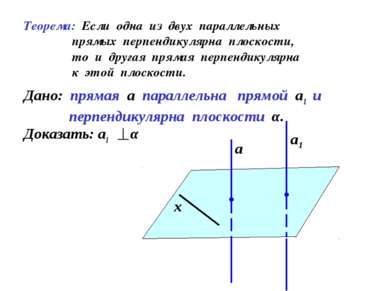Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости. Дано: прямая а параллельна прямой а1 и перпендикулярна плоскости α. Доказать: а1 α а а1 х
Cлайд 7
а b b1 Обратная теорема: Если две прямые перпендикулярны к плоскости, то они параллельны. M c
Cлайд 8
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. а р q O m l А B Q Р L
