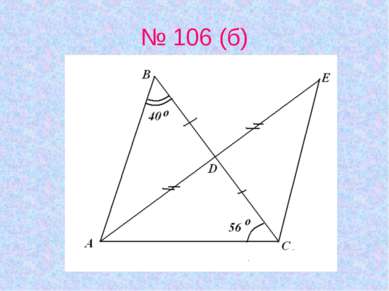
X
Код презентации скопируйте его
Медианы, биссектрисы и высоты треугольника
Скачать эту презентацию
Презентация на тему Медианы, биссектрисы и высоты треугольника
Скачать эту презентациюCлайд 1
Медианы, биссектрисы и высоты треугольника Урок 15.
Cлайд 2
Цели урока: Ввести понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника. Доказать теорему о перпендикуляре Научить строить медианы, биссектрисы и высоты треугольника.
Cлайд 3
Ход урока. огр. момент Проверка домашнего задания. Повторение. Анализ самостоятельной работы. Изучение нового материала.
Cлайд 4
Практическое задание Начертите прямую а и отметьте точку А, не лежащую на прямой
Cлайд 5
Практическое задание Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения обозначьте Н.
Cлайд 6
Теорема о перпендикуляре: Из точки, не лежащей . на прямой, можно провести перпендикуляр к этой прямой и притом только один Отрезок АН – перпендикуляр, проведённый из точки А к прямой а, если: АН ^ a A П a, НО a
Cлайд 7
Дано: а – прямая, A О a Доказать: из точки А к прямой а можно провести перпендикуляр; из точки А к прямой а можно провести единственный перпендикуляр;
Cлайд 8
Практическое задание Постройте треугольник АВС, соедините вершину А с серединой противолежащей стороны М
Cлайд 9
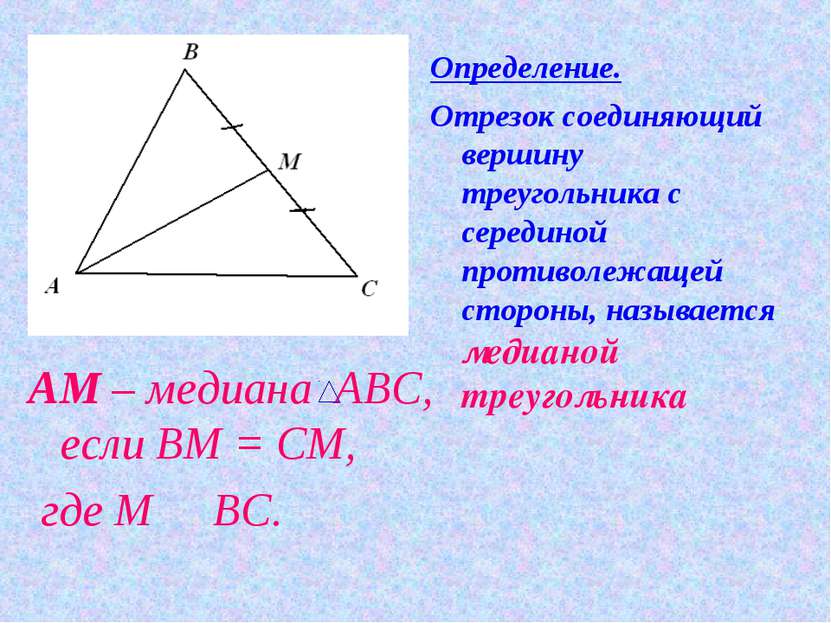
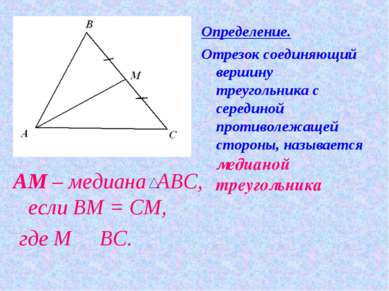АМ – медиана АВС, если ВМ = СМ, где М О ВС. Определение. Отрезок соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника
Cлайд 10
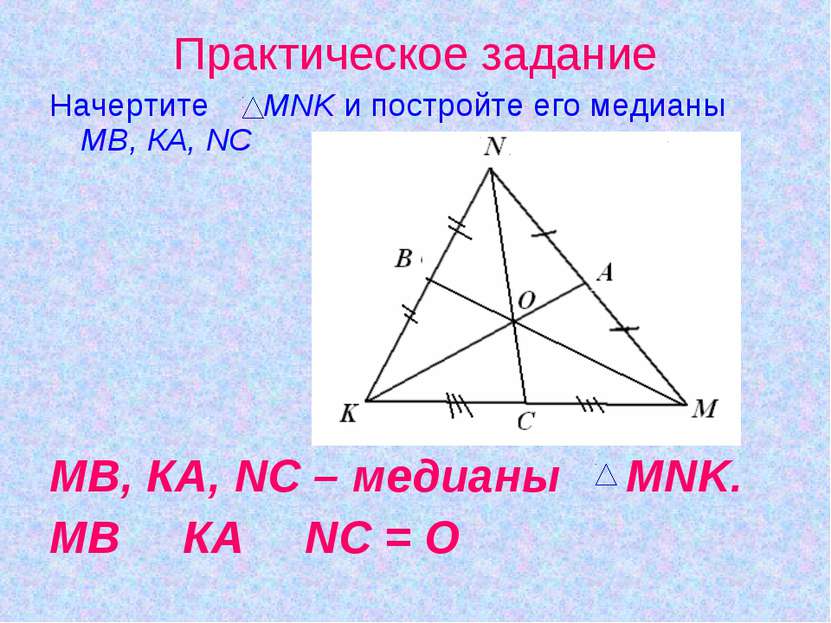
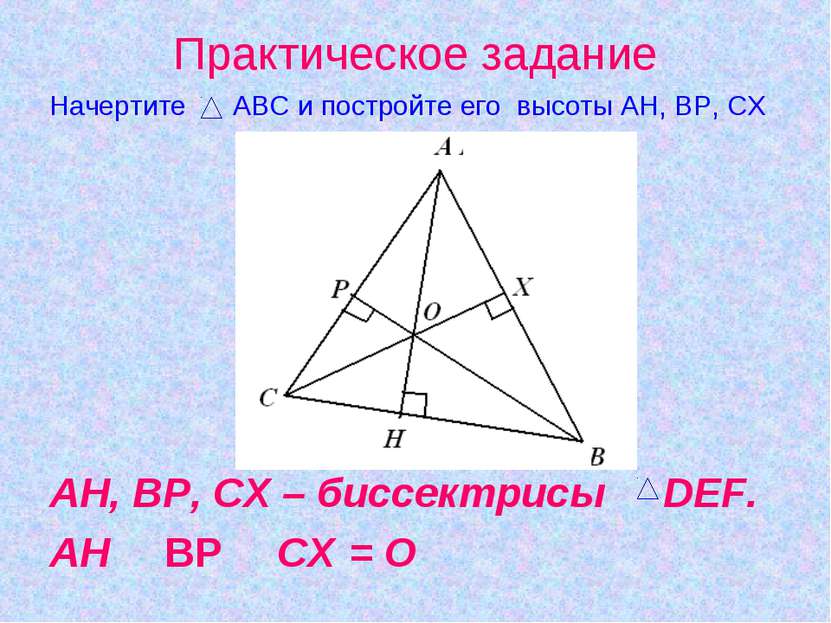
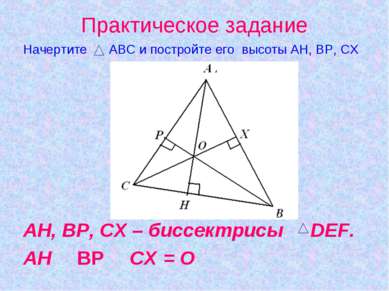
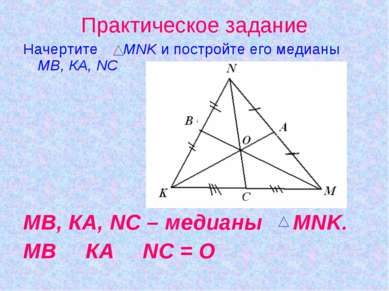Практическое задание Начертите MNK и постройте его медианы МВ, КА, NС МВ, КА, NС – медианы MNK. МВ З КА З NС = О
Cлайд 11
Практическое задание Постройте треугольник АВС, Проведите биссектрису угла В, точку пересечения биссектрисы с противолежащей стороны обозначьте L.
Cлайд 12
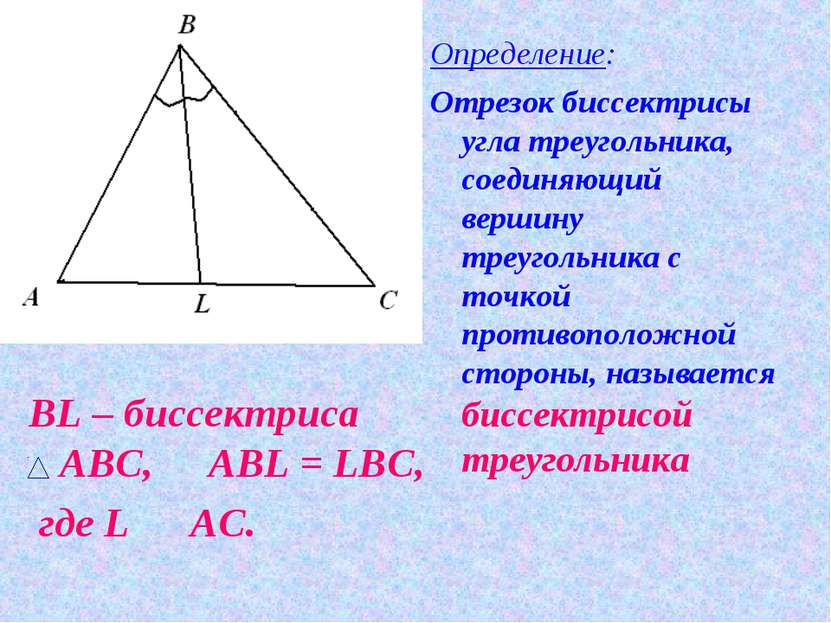
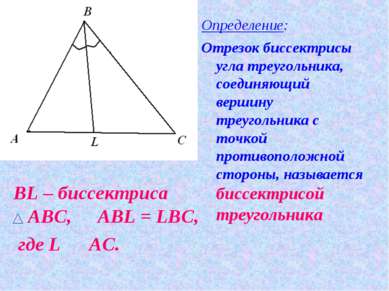BL – биссектриса АВС, Р AВL = LBС, где L О AС. Определение: Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
Cлайд 13
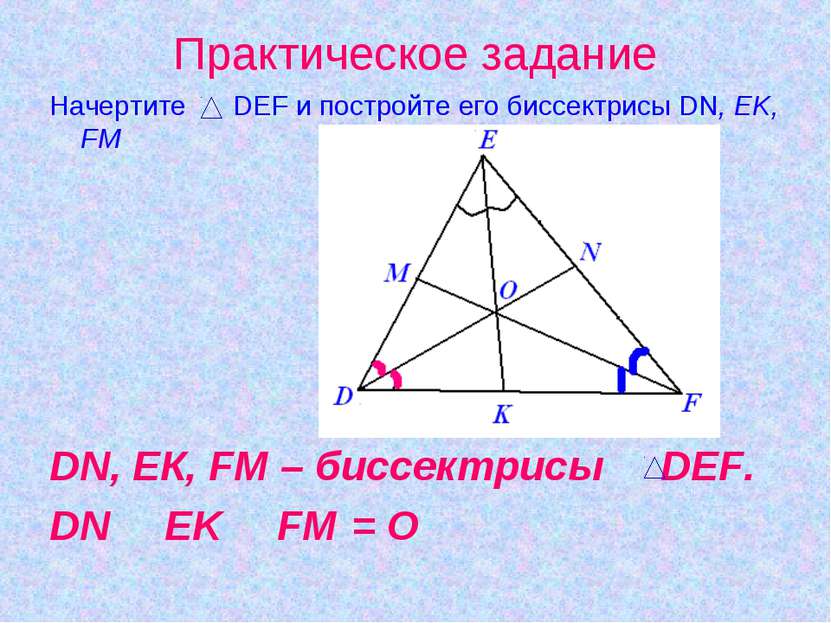
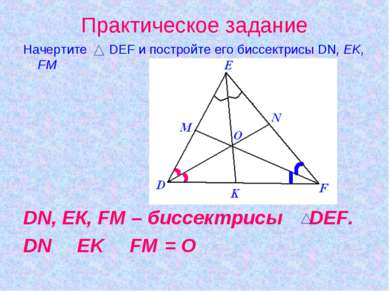Практическое задание Начертите DEF и постройте его биссектрисы DN, EK, FM DN, EК, FM – биссектрисы DEF. DN З EK З FM = О
Cлайд 14
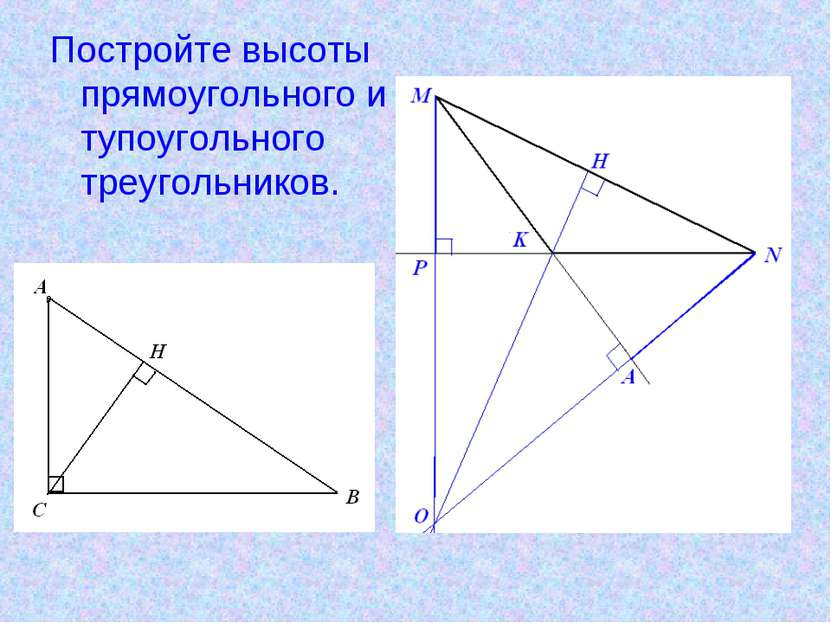
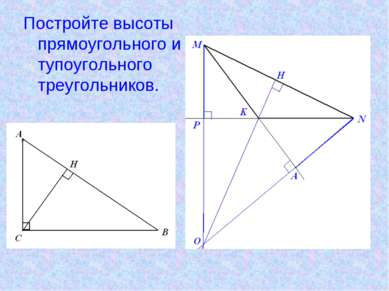
Практическое задание Постройте треугольник АВС, Проведите перпендикуляр АН из точки А к стороне ВС.
Cлайд 15
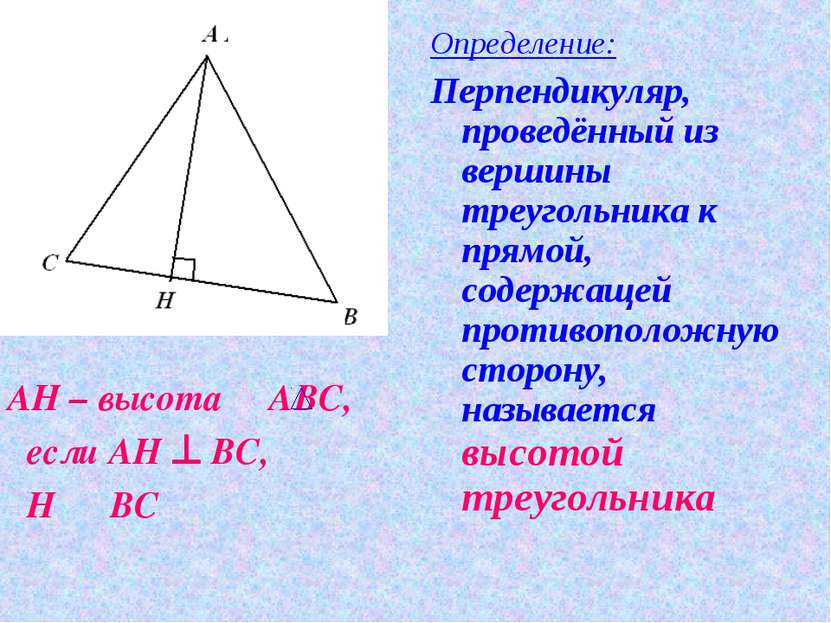
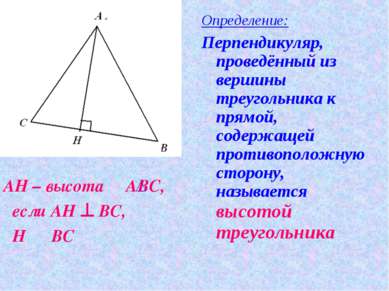АН – высота АВС, если АН ^ ВС, Н О ВС Определение: Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
Cлайд 16
Практическое задание Начертите АВС и постройте его высоты АН, ВР, СХ АН, ВР, СХ – биссектрисы DEF. АН З ВР З СХ = О
Cлайд 17
Постройте высоты прямоугольного и тупоугольного треугольников.
Cлайд 18
Решение задач Устно решите № 60 (а) № 63 из рабочей тетради
Cлайд 19
Письменно решите № 105 (б)
Cлайд 20
№ 105 (б)
Cлайд 21
№ 106 (б)
Cлайд 22
Домашнее задание П. 16, 17 1 уровень - № 61, 62 из рабчей тетради, № 105(а) из учебника 2 уровень - № 64, 65 из рабочей тетради, № 106(а), 100 из учебника
