X
Код презентации скопируйте его
График с точкой разрыва
Скачать эту презентацию
Презентация на тему График с точкой разрыва
Скачать эту презентациюCлайд 1
График с точкой разрыва
Cлайд 2
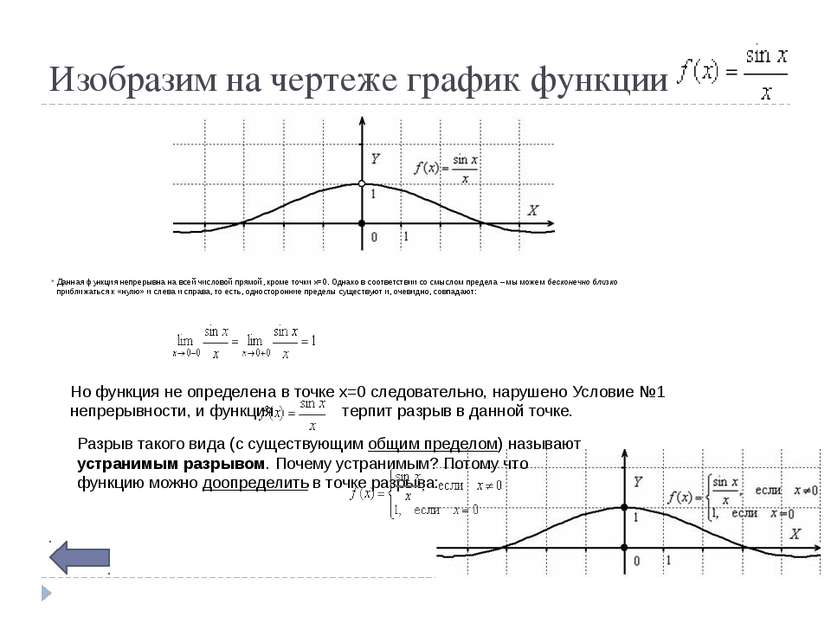
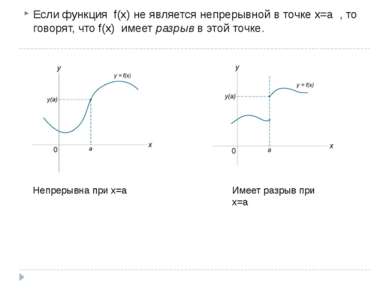Изобразим на чертеже график функции Данная функция непрерывна на всей числовой прямой, кроме точки x=0. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают: Но функция не определена в точке x=0 следовательно, нарушено Условие №1 непрерывности, и функция терпит разрыв в данной точке. Разрыв такого вида (с существующим общим пределом) называют устранимым разрывом. Почему устранимым? Потому что функцию можно доопределить в точке разрыва:
Cлайд 3
Определение: функция непрерывна в точке k , если предел функции в данной точке равен значению функции в этой точке: Определение детализируется в следующих условиях: 1) Функция должна быть определена в точке k, то есть должно существовать значение f(k). 2) Должен существовать общий предел функции . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: . 3) Предел функции в данной точке должен быть равен значению функции в этой точке:
Cлайд 4
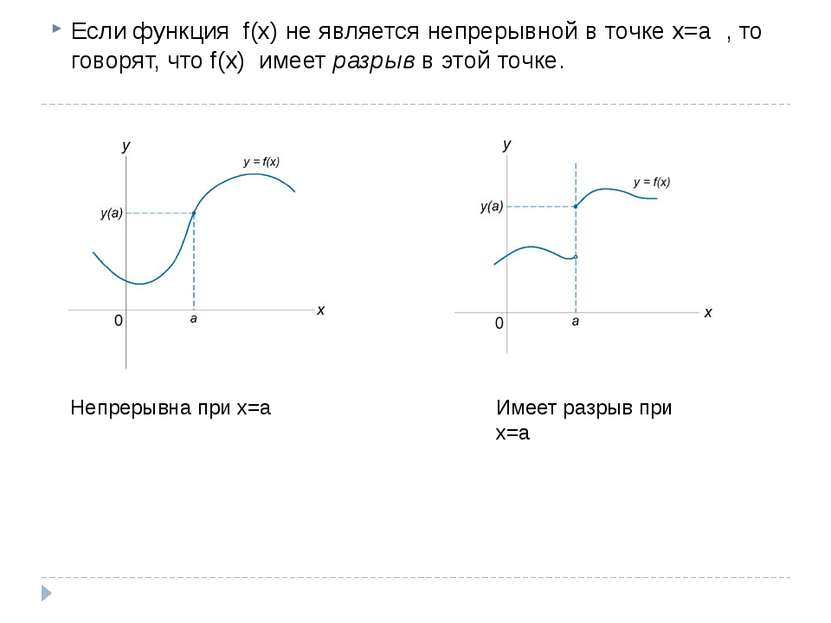
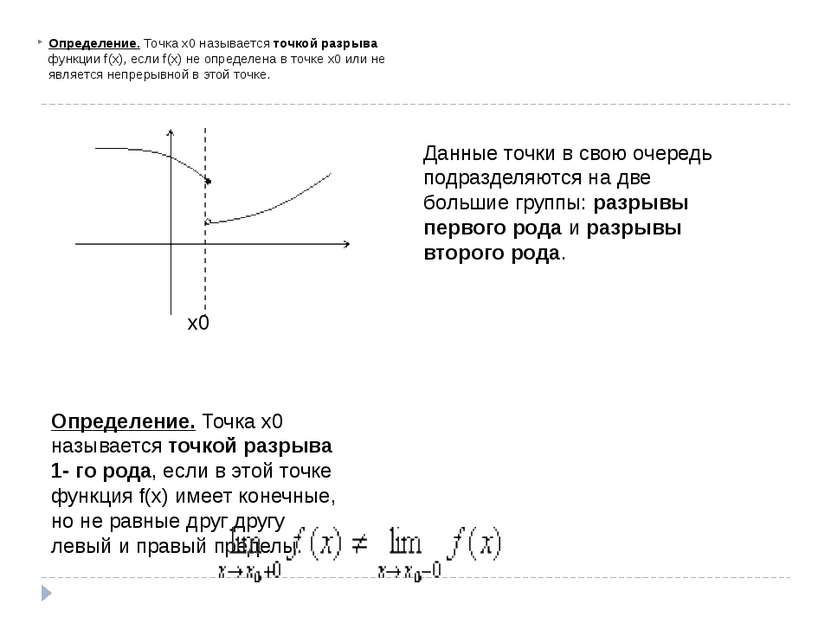
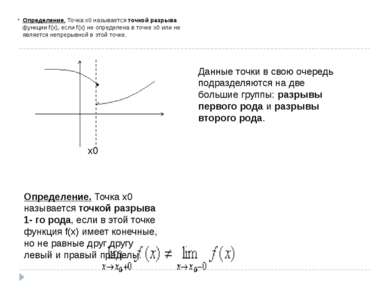Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке. x0 Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы. Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода.
Cлайд 5
Пример. Функция f(x) =– имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к. 1 X Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Cлайд 6
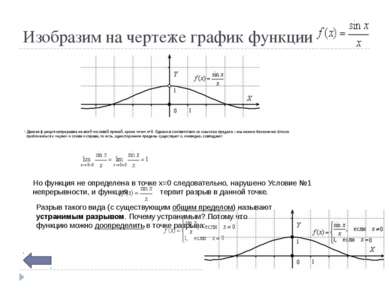Пример. Найти точки разрыва функции Решение. Функция определена и непрерывна при всех x , за исключением точки , где существует разрыв. Исследуем точку разрыва. Так как значения односторонних пределов конечны, то, следовательно, в точке существует разрыв первого рода. График функции схематически показан на рисунке
Cлайд 7
Построение графиков функции с разрывом в Excel Построить график функции , где x в диапазоне от -10 до 10 с шагом 1, a=3, b=4
Cлайд 8
