X
Код презентации скопируйте его
Двоичная система счисления (9 класс)
Скачать эту презентацию
Презентация на тему Двоичная система счисления (9 класс)
Скачать эту презентациюCлайд 1
Степанова М.М., учитель информатики и математики, вторая квалификационная категория МОУ «Гимназия №52»
Cлайд 2
"Мысль выражать все числа десятью знаками, придавая им кроме значения по форме еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна." П.Лаплас
Cлайд 3
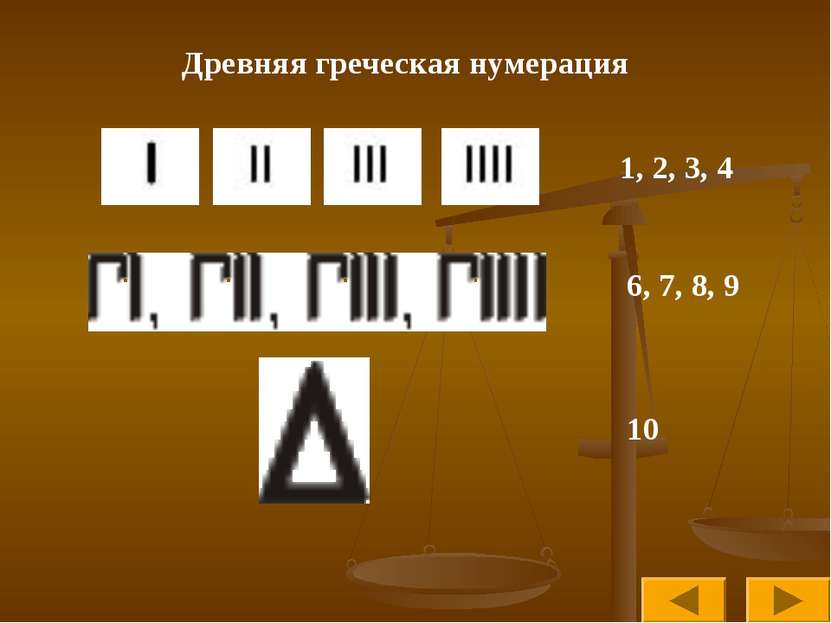
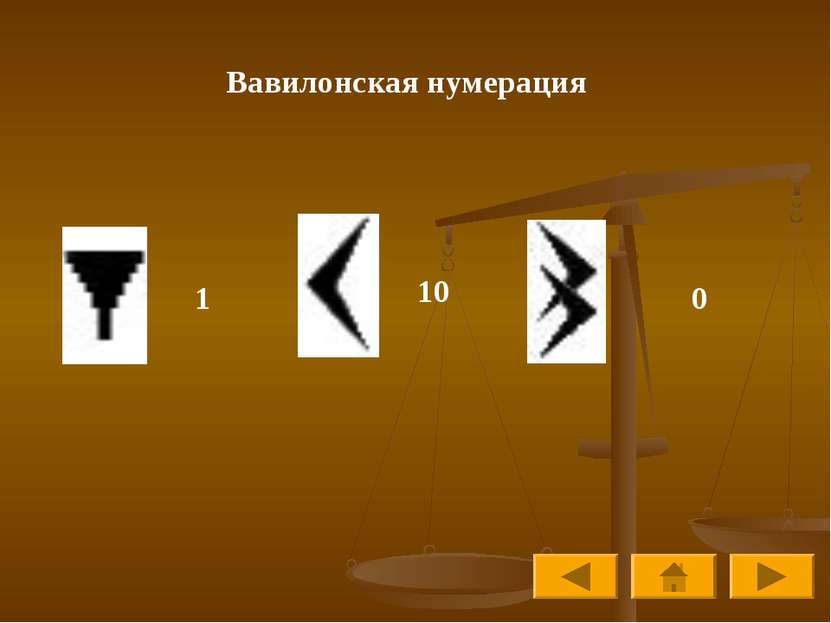
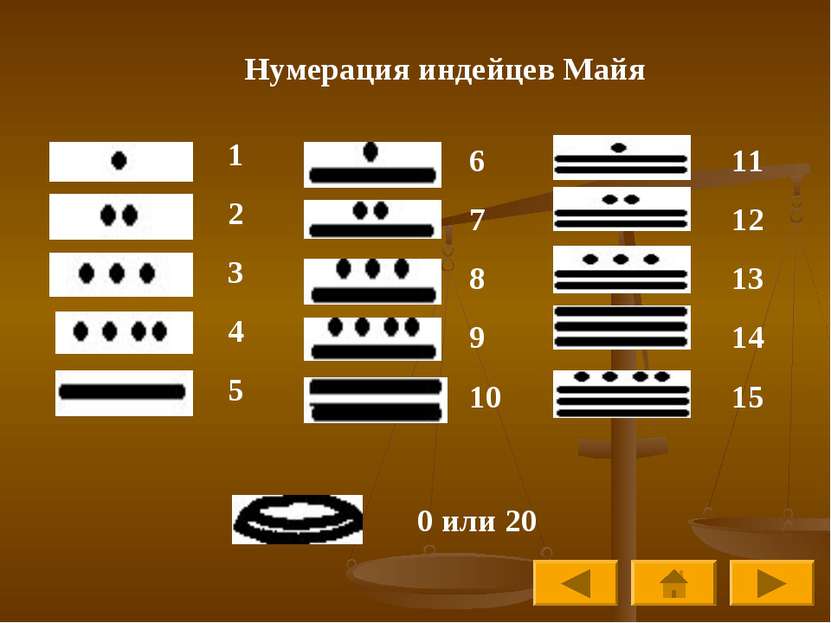
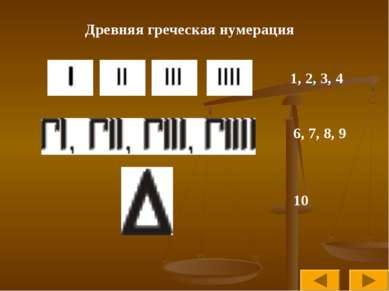
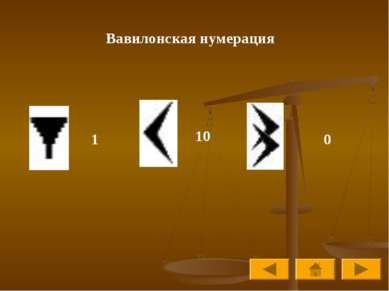
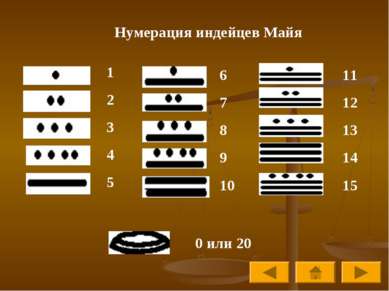
Наиболее известные нумерации мира Древнеегипетская нумерация Древнегреческая нумерация Вавилонская нумерация Нумерация индейцев Майя Старо-Китайская нумерация Славянская кириллическая нумерация Славянская глаголическая нумерация Латинская нумерация Современная арабская нумерация
Cлайд 4
Египетская нумерация 1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем должно быть столько же палочек сколько и в верхнем, или на одну больше.
Cлайд 5
10. Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. 100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.
Cлайд 6
Древняя греческая нумерация 1, 2, 3, 4 6, 7, 8, 9 10
Cлайд 7
Cлайд 8
Вавилонская нумерация 1 10 0
Cлайд 9
Нумерация индейцев Майя 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 или 20
Cлайд 10
Китайская нумерация ° 1 2 3 4 5 6 7 8 9 0 10 100 1000
Cлайд 11
Славянская кириллическая нумерация
Cлайд 12
Славянская глаголическая нумерация 1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 200 300 400 500 600 700 800 900 1000
Cлайд 13
Латинская (Римская) нумерация I 1 V 5 X 10 L 50 C 100 D 500 M 1000
Cлайд 14
Арабская системы счисления Впервые такая система, вернее ее зачатки появилась в Древнем Вавилоне, почти в то же время она была изобретена в Китае, потом в Индии, откуда перекочевала на Аравийский полуостров, а затем и в Европу. Здесь эту систему счисления назвали Арабской, и под этим именем она разошлась по всему миру. Так что, говоря "арабские числа" надо иметь в виду, ну, хотя бы индийские.
Cлайд 15
Позиционные системы счисления Система счисления Алфавит языка Десятичная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Двоичная 0, 1 Восьмеричная 0, 1, 2, 3, 4, 5, 6, 7 Шестнадцатеричная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15)
Cлайд 16
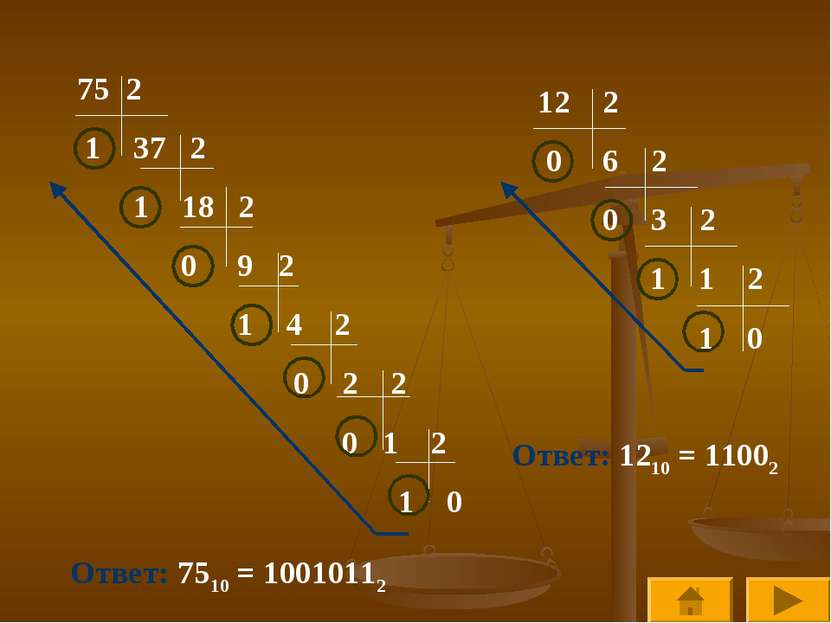
Правило. Для перевода целого числа N в систему счисления с основанием q необходимо разделить N на q с остатком. Затем неполное частное, полученное от этого деления снова разделить на q с остатком и т.д., пока последнее частное не станет равным нулю. Получившиеся остатки выписать в обратном порядке.
Cлайд 17
Примеры: Переведем числа 75 и 12 из десятичной системы счисления в двоичную.
Cлайд 18
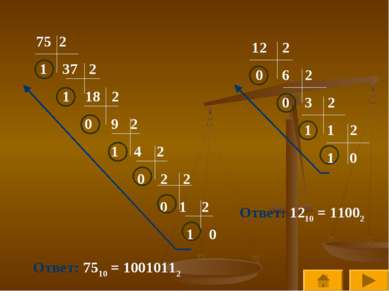2 1 37 2 1 18 2 0 9 2 1 4 2 0 2 2 0 1 2 1 0 Ответ: 7510 = 10010112 12 2 0 6 2 0 3 2 1 1 2 1 0 Ответ: 1210 = 11002
Cлайд 19
Задание. Переведите десятичные числа в двоичную. 1 вариант - 25 и 42 2 вариант - 35 и 30
Cлайд 20
Ответы: 2510 = 110012 3510 = 1000112 4210 =1010102 3010 = 111102
Cлайд 21
Правило. Для перевода правильной десятичной дроби N в систему счисления с основанием q необходимо умножить N на q, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, до тех пор пока дробная часть не станет равной нулю или не будет достигнута требуемая точность. Получившиеся результате произведения целые части дроби выписать сверху вниз.
Cлайд 22
Примеры: Переведем число 0,1875 и 0,12 (с точностью до 6 знаков) из десятичной системы счисления в двоичную.
Cлайд 23
0 1875 0 375 0 75 1 5 1 0 Ответ: 0,187510 = 0,00112 0 12 0 24 0 48 0 96 1 92 1 84 1 68 … … Ответ: 0,1210 = 0,0001112
Cлайд 24
Задание. Переведите десятичные дробные числа в двоичную. 1 вариант - 0,25 и 0,3 (с точностью 4 знака) 2 вариант - 0,75 и 0,4 (с точностью 4 знака)
Cлайд 25
Ответы: 0,2510 = 0,012 0,7510 = 0,112 0,310 = 0,01002 0,410 = 0,01102
Cлайд 26
Правило. Для перевода числа х (хq = апап-1…а0,а-1а-2…а-т) из системы счисления с основанием q (q=2, 8 или 16) в десятичную систему счисления необходимо вычислить значение многочлена х10=ап qп+ ап-1 qп-1+…+а0 q0+а-1 q-1+а-2 q-2+…+а-т q-т.
Cлайд 27
Примеры: Переведем число 111001,12 в десятичную систему счисления. 111001,12 = 1. 25 + 1.24 + 1.23 + 0.22 + 0.21 + 1.20 + 1.2-1 = 57,510 Решения:
Cлайд 28
Задание: Переведите числа в десятичную систему счисления. 1 вариант - 1 111, 012 2 вариант - 10 000, 0012
Cлайд 29
Ответы: 1 111, 012 = 15, 2510 10 000, 0012 = 16, 12510
Cлайд 30
Домашнее задание. Переведите числа из десятичной системы счисления в двоичную: 100,45 99 0,8125 2. Переведите число в десятичную систему счисления: 110 000, 1112
Cлайд 31
Дополнительное задание. Переведите в двоичную. 200410 и 300410 Ответы: 200410 = 11 111 010 1002 300410 = 101 110 111 1002
Cлайд 32
1 2 3 4 5 6 7 8 9 к л а в и а т у р а д ж о й с т и к м о н и т о р п р и н т е р п а м я т ь т ю н е р д и с к е т а с к а н е р п р о ц е с с о р
