X
Код презентации скопируйте его
Двоичная система счисления
Скачать эту презентацию
Презентация на тему Двоичная система счисления
Скачать эту презентациюCлайд 1
Двоичная система счисления
Cлайд 2
Повторим тему «Системы счисления»
Cлайд 3
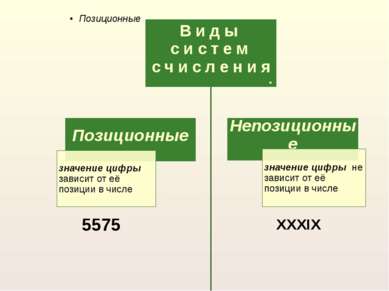
Основные понятия систем счисления Система счисления - это способ записи чисел и связанные с ними способы выполнения вычислений. Число - это некоторая величина Цифра - это символы, участвующие в записи числа Алфавит - совокупность различных цифр, используемых для записи числа
Cлайд 4
5575 XXXIX
Cлайд 5
Единичная («палочная») система счисления (период палеолита, 10-11 тысяч лет до н.э.) Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе.
Cлайд 6
= 3 4 5 Иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Древнеегипетская система счисления (ок.2850 до н.э.)
Cлайд 7
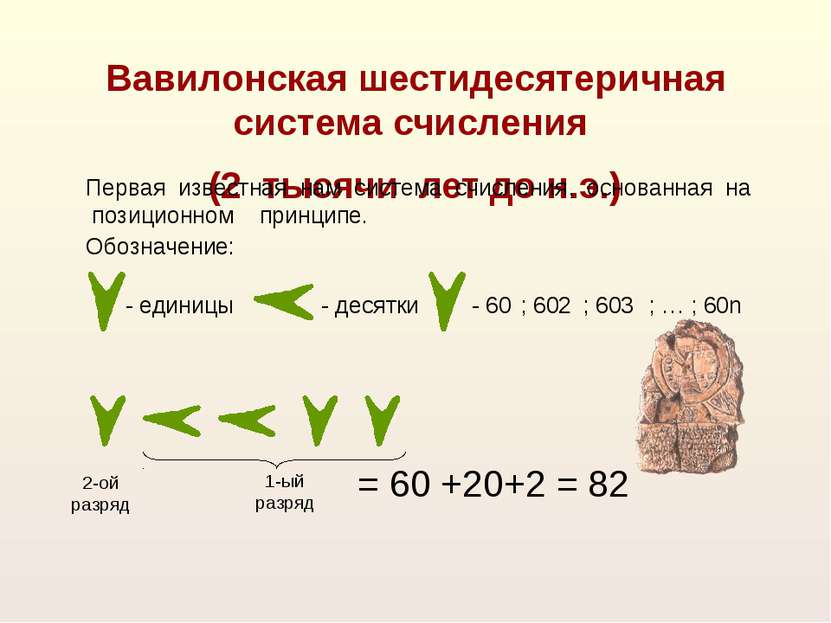
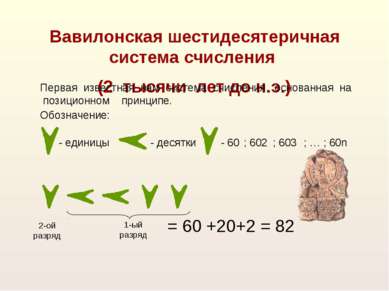= 60 +20+2 = 82 2-ой разряд 1-ый разряд Вавилонская шестидесятеричная система счисления (2 тысячи лет до н.э.) Первая известная нам система счисления, основанная на позиционном принципе. - единицы - десятки Обозначение:
Cлайд 8
X X X I I = 32 D X L I I = 542 Значение цифры не зависит от ее положения в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа - прибавляется. Например, IX = 9, а XI=11. Какие числа записаны римскими цифрами? Величина числа определяется как сумма или разность цифр в числе. Римская система счисления (500 лет до н.э.) В качестве цифр в римской системе используются:
Cлайд 9
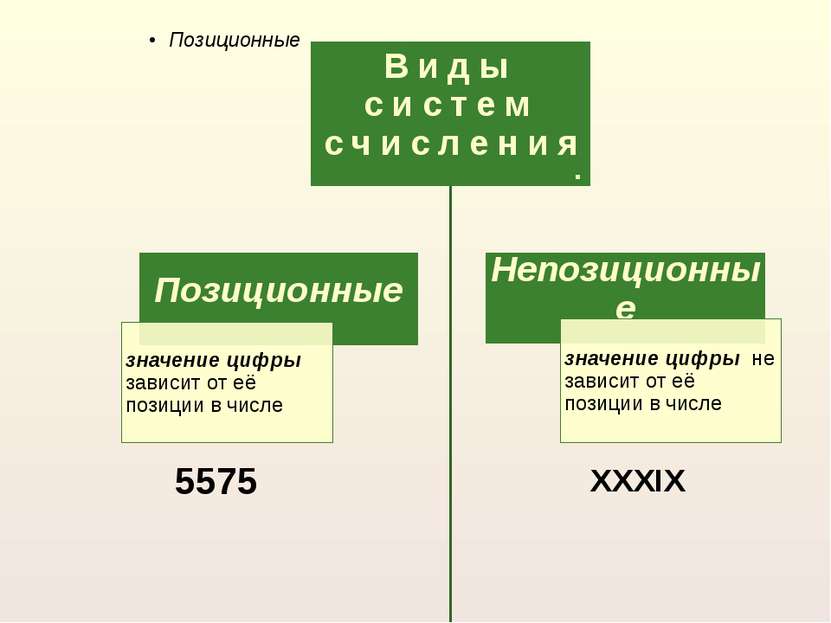
– основание (p) Набор всех цифр для записи числа – алфавит Количество цифр для записи числа Позиционные системы могут иметь различный алфавит (2,3,4 знака). Позиционные системы счисления Каждая позиционная система счисления имеет определенный алфавит и основание.
Cлайд 10
Алфавиты систем счисления Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из р цифр. При р > 10 к десяти арабским цифрам добавляют латинские буквы. Позиция цифры в числе называется разрядом. Основание Название Алфавит р= 2 Двоичная 0 1 р= 3 Троичная 0 1 2 р= 8 Восьмеричная 0 1 2 3 4 5 6 7 р= 16 Шестнадцатеричная 0 1 2 3 4 5 6 7 8 9A B C D E F
Cлайд 11
Представление информации в компьютере В каждой такой «клетке» хранится только одно из двух значений : нуль или единица. Каждая «клетка» памяти компьютера называется битом. Цифры 0 и 1, хранящиеся в «клетках» компьютера, называются значениями битов. 0 1 и Машинную память удобно представить в виде листа в клетку.
Cлайд 12
5555=5000+500+50+5=5*1000+5*100+5*10+5*1=5*103+5*102+5*101+5*100 456327=4*100000+5*10000+6*1000+3*100+2*10+7*1=4*105+5*104+6*103+3*102+2*101+7*100 Рассмотрим десятичную систему счисления Развёрнутая форма записи числа
Cлайд 13
Позиция цифры в числе называется разрядом. Aq = an-1 qn-1 + … + a1 q1 + a0 q0 + a-1 q-1 + … + a-m q-m, где q — основание системы счисления (количество используемых цифр) Aq — число в системе счисления с основанием q a — цифры многоразрядного числа Aq n (m) — количество целых (дробных) разрядов числа Aq Развёрнутая форма записи числа
Cлайд 14
11012=1*23+1*22+0*21+1*20=1*8+1*4+0*2+1*1=13 111000112=? Рассмотрим двоичную систему счисления Перевод двоичного числа в десятичное
Cлайд 15
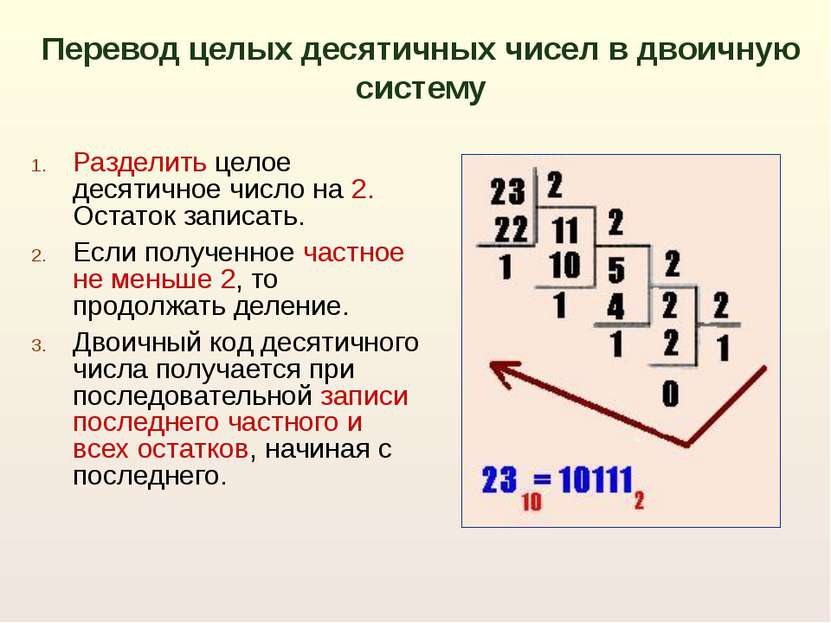
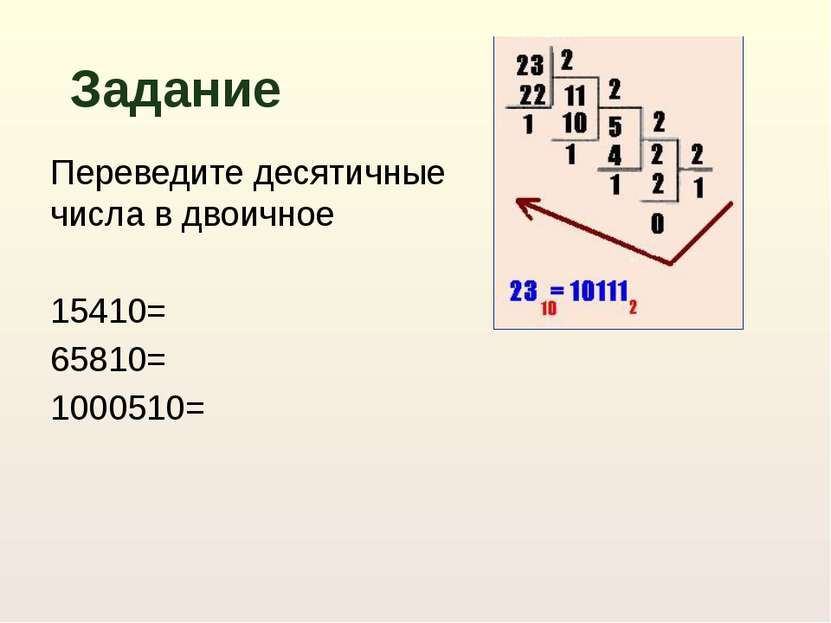
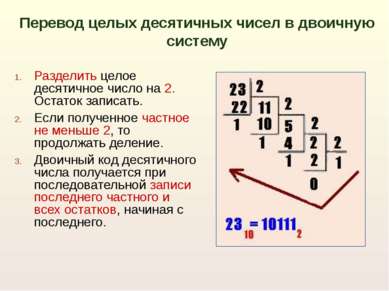Разделить целое десятичное число на 2. Остаток записать. Если полученное частное не меньше 2, то продолжать деление. Двоичный код десятичного числа получается при последовательной записи последнего частного и всех остатков, начиная с последнего. Перевод целых десятичных чисел в двоичную систему
Cлайд 16
Переведите десятичные числа в двоичное 15410= 65810= 1000510= Задание
Cлайд 17
Арифметика двоичных чисел 0+0= 0+1= 1+0= 1+1= 0*0= 0*1= 1*0= 1*1= 0 10 0 0 0 1 1 1
Cлайд 18
§16 Стр. 100 задание 4, 5 и 6 Домашнее задание
