X
Код презентации скопируйте его
Применение линейного программирования в математических моделях
Скачать эту презентацию
Презентация на тему Применение линейного программирования в математических моделях
Скачать эту презентациюCлайд 1
*/23 Лекция 3. Применение линейного программирования в математических моделях Содержание лекции: Принцип оптимальности в планировании и управлении Задача линейного программирования Симплексный метод Экономические приложения линейного программирования Программное обеспечение линейного программирования
Cлайд 2
*/23 Литература Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — глава 2. Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001. Канторович Л.В. Экономический расчёт наилучшего использования ресурсов. М.: Изд-во АН СССР, 1960. Светлов Н.М., Светлова Г.Н. Построение и решение оптимизационных моделей средствами программ MS Excel и XA: Методические указания для студентов экономического факультета / РГАУ – МСХА имени К.А. Тимирязева. М., 2005. http://svetlov.timacad.ru/umk1/xa_1.doc Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 3
*/23 3.1. Принцип оптимальности в планировании и управлении Принцип оптимальности предполагает следующее: наличие определённых ресурсов наличие определённых технологических возможностей цель хозяйственной деятельности извлечение прибыли удовлетворение потребностей предотвращение угрозы накопление знаний и т.д. Суть принципа: планировать хозяйственную деятельность таким образом, чтобы при имеющихся ресурсах и технологиях не существовало способа достичь цели в большей степени, чем это предусматривает план В полной мере этот принцип может быть реализован только с помощью экономико-математических моделей Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 4
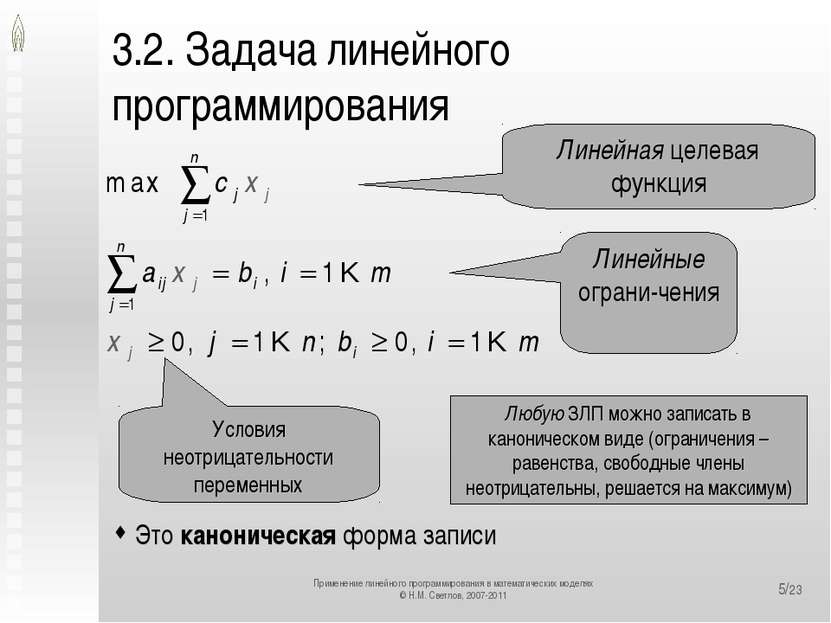
*/23 3.2. Задача линейного программирования Это развёрнутая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности переменных Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 5
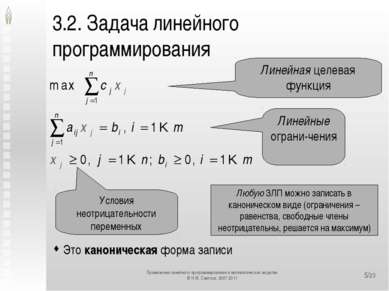*/23 3.2. Задача линейного программирования Это каноническая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности переменных Любую ЗЛП можно записать в каноническом виде (ограничения – равенства, свободные члены неотрицательны, решается на максимум) Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 6
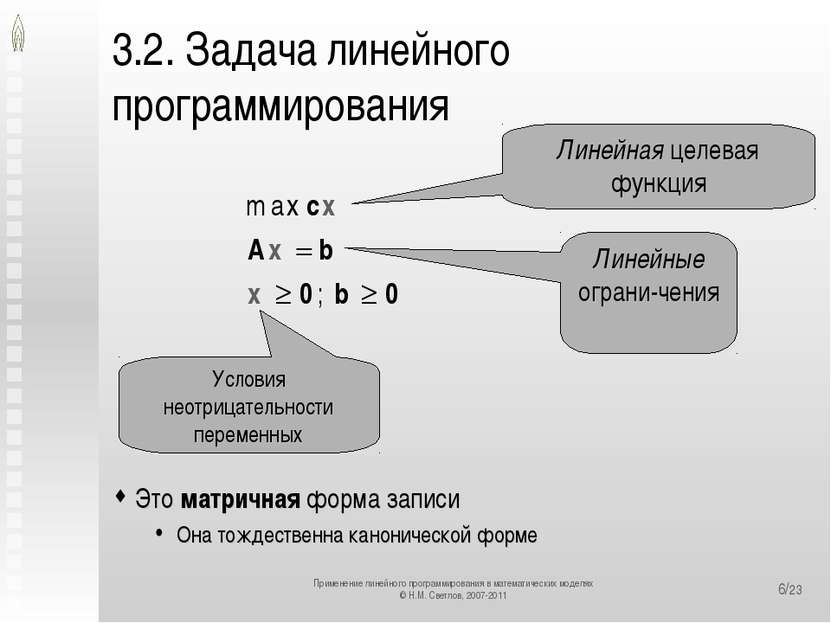
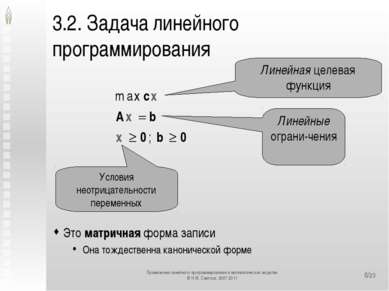*/23 3.2. Задача линейного программирования Это матричная форма записи Она тождественна канонической форме Линейная целевая функция Линейные ограни-чения Условия неотрицательности переменных Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 7
*/23 3.2. Задача линейного программирования Это стандартная форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности переменных Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 8
*/23 3.2. Любой вектор x, удовлетворяющий ограничениям и условиям неотрицательности (безотносительно к целевой функции), называется допустимым решением Если допустимых решений не существует, говорят, что система ограничений несовместна Областью допустимых решений (ОДР) называется множество, включающее все допустимые решения данной ЗЛП Допустимое решение x*, доставляющее наибольшее значение целевой функции среди всех допустимых решений данной ЗЛП, называется оптимальным решением часто его называют просто решением ЗЛП Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 9
*/23 3.2. ЗЛП может: не иметь ни одного оптимального решения допустимой области не существует – система ограничений не совместна z = max(x1+x2|x1+5x2 1, x1+x2 5, x1 0, x2 0) допустимая область существует, но не ограничивает целевую функцию z = max(2x1+x2|0.1x1+0.1x2 5, x1 0, x2 0) иметь одно оптимальное решение z = max(x1+x2|0.1x1+0.2x2 5, x1 0, x2 0) x1=50, x2 =0; z = 50 иметь бесконечно много оптимальных решений z = max(x1+x2|0.1x1+0.1x2 5, x1 0, x2 0) x1=50, x2 =0; z = 50 … x1=0, x2 =50; z = 50 Компактная запись Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 10
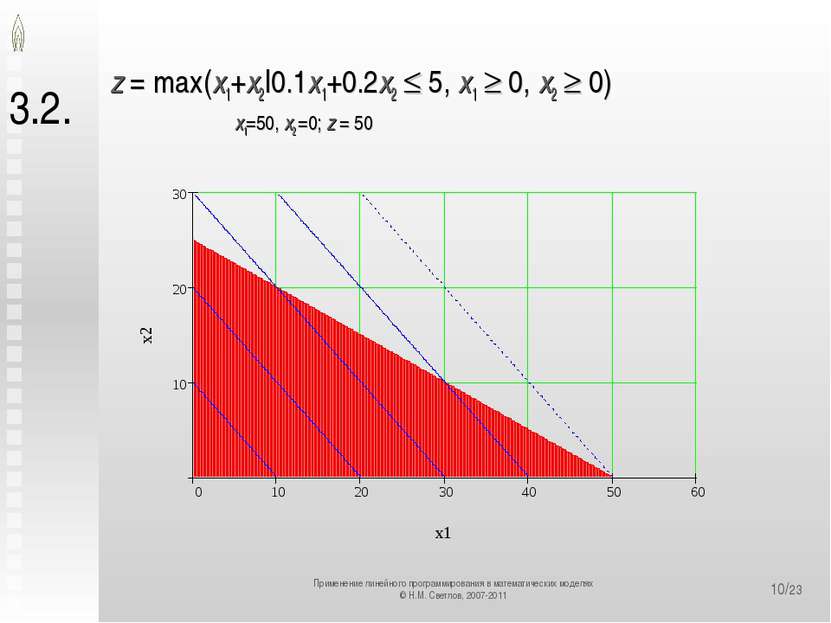
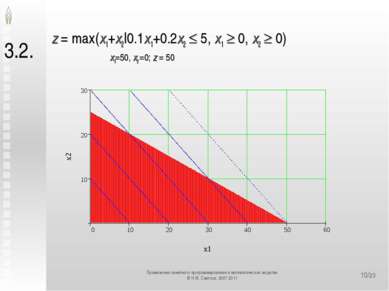*/23 3.2. z = max(x1+x2|0.1x1+0.2x2 5, x1 0, x2 0) x1=50, x2 =0; z = 50 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 11
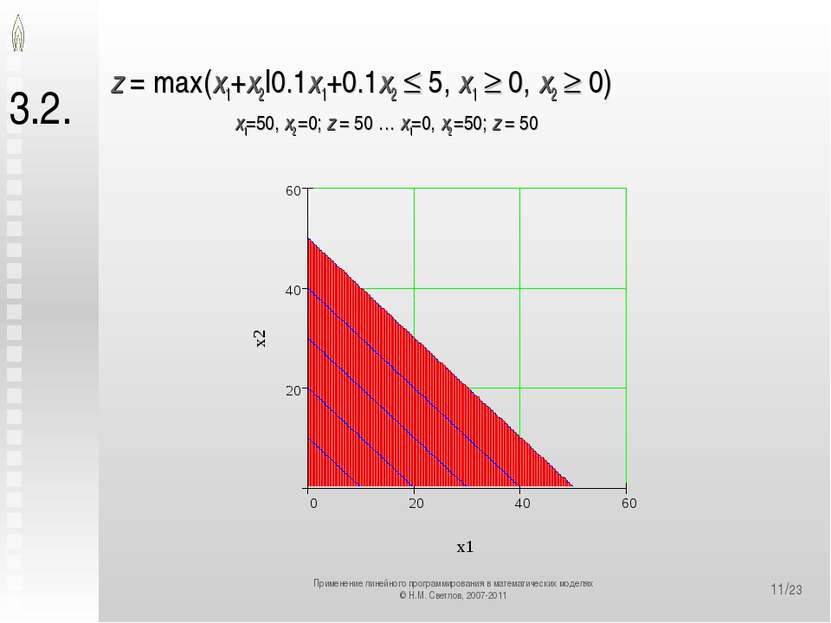
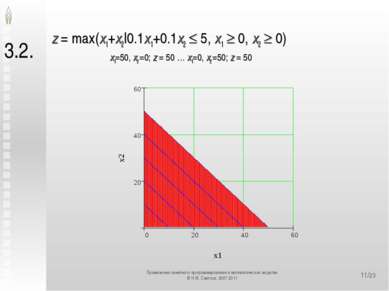*/23 3.2. z = max(x1+x2|0.1x1+0.1x2 5, x1 0, x2 0) x1=50, x2 =0; z = 50 … x1=0, x2 =50; z = 50 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 12
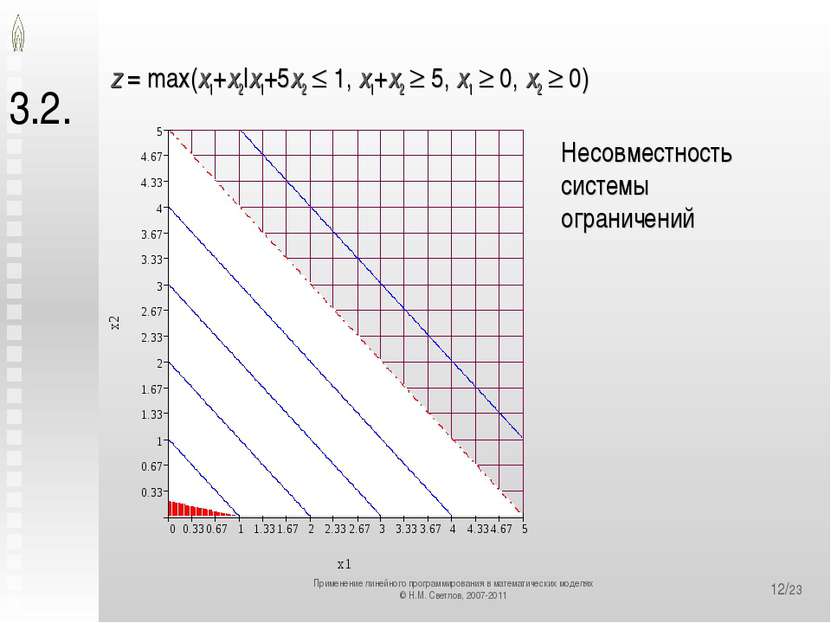
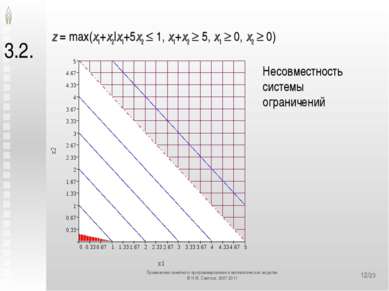*/23 3.2. z = max(x1+x2|x1+5x2 1, x1+x2 5, x1 0, x2 0) Несовместность системы ограничений Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 13
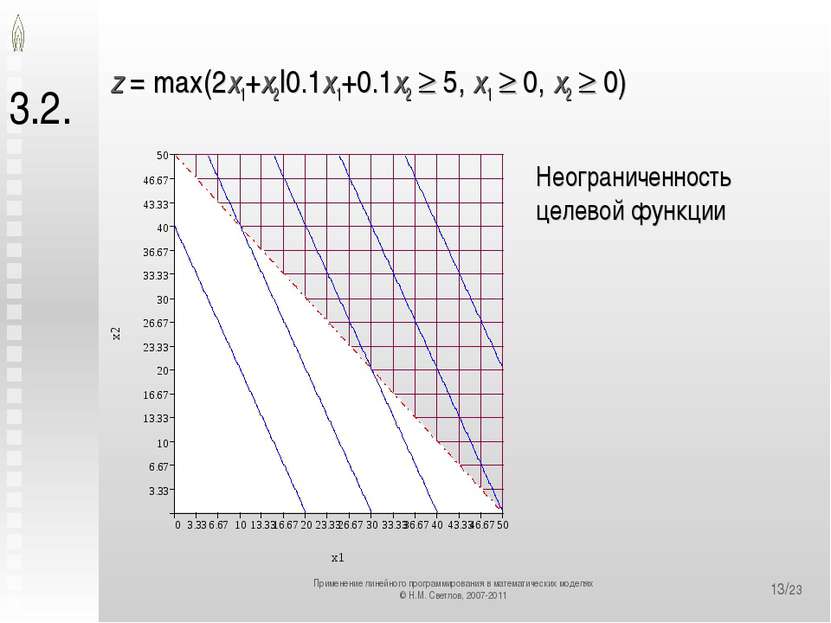
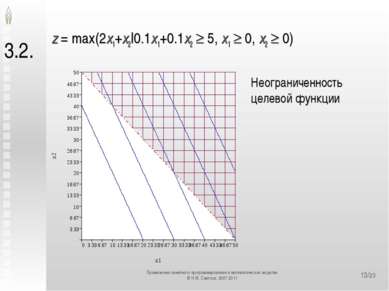*/23 3.2. z = max(2x1+x2|0.1x1+0.1x2 5, x1 0, x2 0) Неограниченность целевой функции Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 14
*/23 3.3. Симплексный метод Исходные условия применения симплексного метода ЗЛП записана в канонической форме Её ограничения линейно независимы Известно опорное решение, в котором: имеется не более m ненулевых переменных задача содержит n переменных и m ограничений все ограничения выполняются m переменных, называемых базисными (среди которых все ненулевые) выражены через: n–m переменных, называемых свободными (каждая равна нулю) свободный член ограничения Результат этой процедуры записан в начальную (первую, исходную) симплексную таблицу Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 15
*/23 3.3. z = max(x1+x2|0.1x1+0.2x2 5, x1–2x2 75, x1 0, x2 0) x1=50, x2 =0; z = 50 Каноническая форма: max x1+x2 0.1x1+0.2x2+x3 = 5 x1–2x2 +x4 = 75 x1 0, x2 0, x3 0, x4 0 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 j =1 j = 2 j = 3 i =1 j = 4 i =2 b cj , ci 1 1 0 0 0 i = 1 0.1 0.2 1 0 5 i = 2 1 -2 0 1 75 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 16
*/23 В таблице выделены жирным шрифтом 3.3. Разрешающий столбец: столбец с наибольшим положительным cj если положительного cj нет, достигнут оптимум Разрешающая строка: для всех положительных aij в выбранном столбце считаем bi /aij если положительных нет, ц.ф. не ограничена выбираем строку, где это значение минимально Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 j =1 j = 2 j = 3 i =1 j = 4 i =2 b cj , ci 1 1 0 0 0 i = 1 0.1 0.2 1 0 5 i = 2 1 -2 0 1 75 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 17
*/23 3.3. Выполняем обыкновенные жордановы исключения во всей таблице: для строк i i' : aijнов = aij – ai'jaij' /ai'j' , где i' и j' – координаты выбранных (разрешающих) строки и столбца для строки i =i' : aijнов = aij /ai'j' Положительных cj больше нет – достигнут оптимум (в больших задачах для этого требуются тысячи итераций) Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 j =1 i =1 (50) j = 2 (0) j = 3 (0) j = 4 i =2 (25) b cj , ci 0 -1 -10 0 -50 i = 1 1 2 10 0 50 i = 2 0 -4 -10 1 25 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 18
*/23 3.3. Опорное решение может быть получено по следующей процедуре: Выбираем произвольный набор базисных переменных и выражаем их через свободные Если строк с отрицательными свободными членами нет – опорное решение получено; иначе – п.3. Одну из таких строк выбираем в качестве вспомогательной целевой функции и проводим по ней процедуру решения на минимум, используя алгоритм симплекс-метода Если в качестве разрешающей выбирается строка с отрицательным свободным членом, то разрешающий элемент тоже должен быть отрицательным для всех aij в выбранном столбце считаем bi /aij наименьшее положительное значение этого отношения указывает разрешающую строку если положительных нет, выбираем другую строку с отрицательным свободным членом в качестве вспомогательной целевой функции если таковых не находится, опорных решений не существует (целевая функция не ограничена множеством допустимых решений) Если оптимум достигнут при отрицательном свободном члене – система ограничений несовместна; иначе – п.5 Как только достигнуто положительное значение свободного члена, переходим к п.2. Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 19
*/23 3.3. В некоторых случаях алгоритм симплексного метода может зацикливаться. Пути преодоления этой проблемы описаны в рекомендуемой литературе. Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 20
*/23 3.4. Экономические приложения линейного программирования Матрица потребности в ресурсах для обеспечения единичного объёма производства в каждой отрасли. Строки – ресурсы, столбцы – отрасли. Объёмы невоспроизводимых ресурсов (земельные угодья, трудовые ресурсы, запасы полезных ископаемых и т.п.), имеющиеся в распоряжении народного хозяйства Матрица затрат (+) и выпуска (-) ресурсов при единичном объёме производства в каждой отрасли. Строки – ресурсы, столбцы – отрасли. Вектор, состоящий из нулей Матрица выпуска (+) конечной продукции при единичном объёме производства в каждой отрасли. Строки – виды продукции, столбцы – отрасли. Вектор объёмов потребления каждого вида конечной продукции при единичном (стандартном) уровне удовлетворения потребностей Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 21
*/23 3.4. Экономические приложения линейного программирования Вектор цен продукции (за вычетом НДС), руб./ед. Вектор цен ресурсов (включая НДС), руб./ед. Матрица затрат ресурсов на производство и реализацию единицы продукции, ед.рес./ед.прод. Вектор наличия (начальных запасов) ресурсов Матрица объёмов обязательств, выполняемых вследствие реализации единицы продукции каждого вида Объёмы обязательств, имеющихся у предприятия и учитываемых при оптимальном планировании (выполнение которых зависит от составленного плана) Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
Cлайд 22
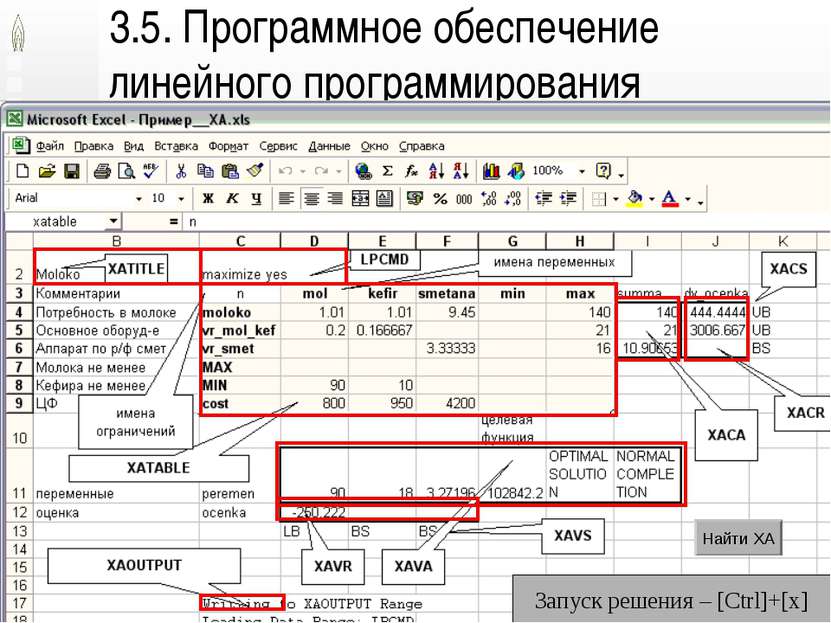
Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007 */23 3.5. Программное обеспечение линейного программирования Запуск решения – [Ctrl]+[x] Найти XA Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007
Cлайд 23
*/23 3.5. Два способа установки XA Если есть права доступа к каталогу C:\WINDOWS копируем туда файлы CXA32.DLL и CAXA32.DLL Иначе копируем файлы CXA32.DLL и CAXA32.DLL в ту папку, в которой решаем модель после вызова файла модели нажимаем кнопку и указываем расположение любого из этих файлов это действие повторяется при каждом вызове Excel Антивирус Касперского блокирует выполнение XA При первом вызове программы следует в ответ на предупреждение антивируса дать ему указание разрешать выполнение данной программы Найти XA Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011 Применение линейного программирования в математических моделях © Н.М. Светлов, 2007-2011
