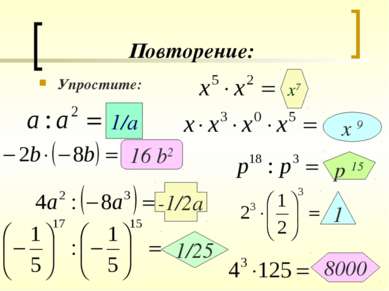X
Код презентации скопируйте его
Функция у = х п и ее свойства
Скачать эту презентацию
Презентация на тему Функция у = х п и ее свойства
Скачать эту презентациюCлайд 1
Функция у = х п и ее свойства. МОУ СОШ №256 г.Фокино Каратанова Марина Николаевна.
Cлайд 2
Повторение: Какое выражение надо подставить вместо * , чтобы получилось тождество: 1. х 4 х10 х 3 х 4 2. 3. 4.
Cлайд 3
Повторение: Упростите: х7 1/а х 9 16 b2 р 15 -1/2а 1 1/25 8000
Cлайд 4
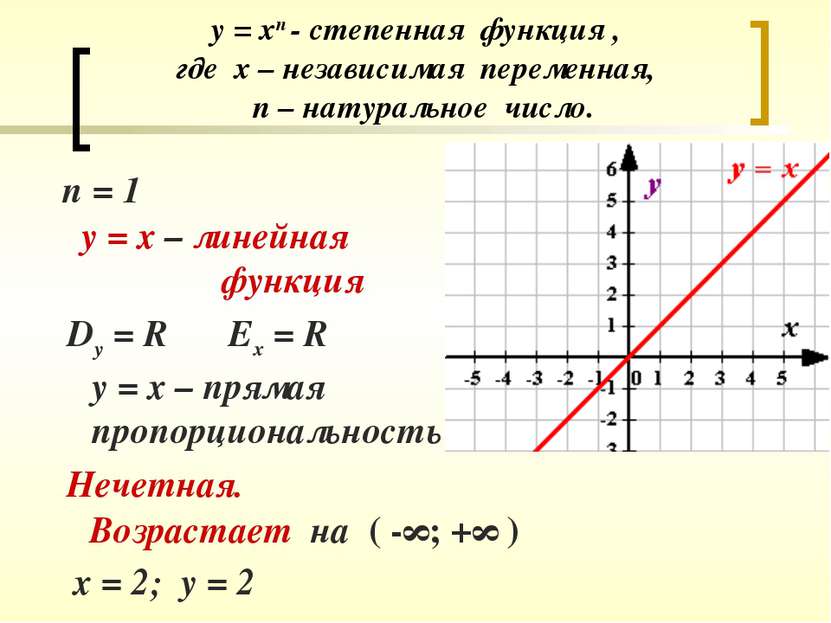
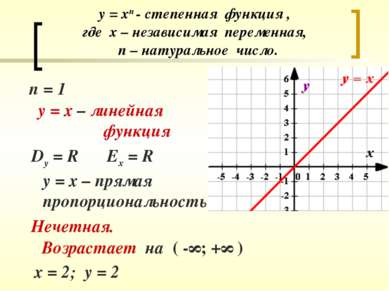у = хп - степенная функция , где х – независимая переменная, п – натуральное число. п = 1 у = х – линейная функция Dy = R у = х – прямая пропорциональность х = 2; у = 2 Нечетная. Ех = R Возрастает на ( -∞; +∞ )
Cлайд 5
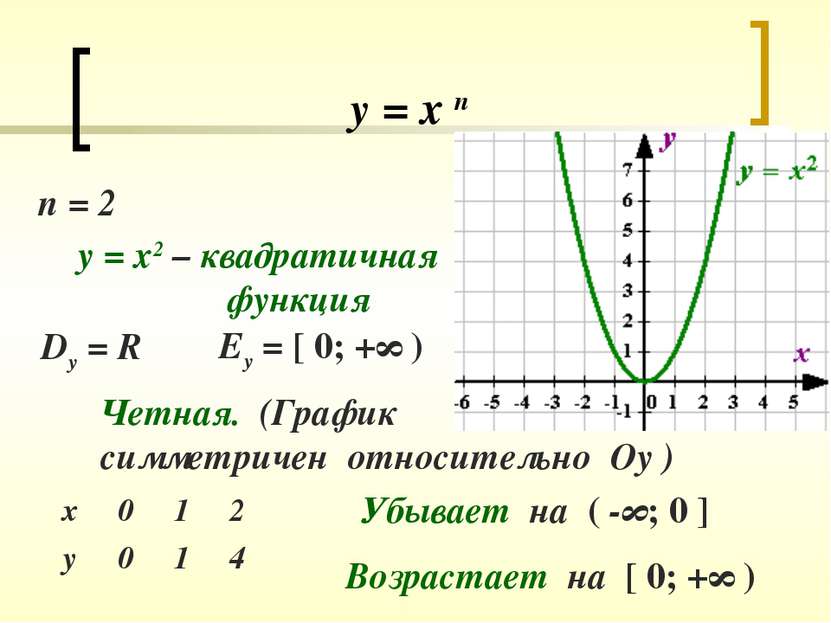
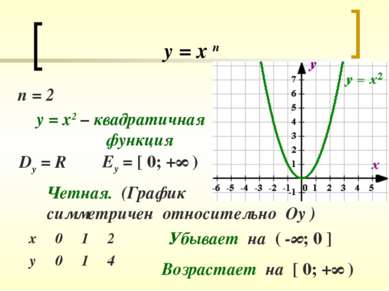у = х п п = 2 у = х2 – квадратичная функция Dy = R Еу = [ 0; +∞ ) Четная. (График симметричен относительно Оу ) Убывает на ( -∞; 0 ] Возрастает на [ 0; +∞ )
Cлайд 6
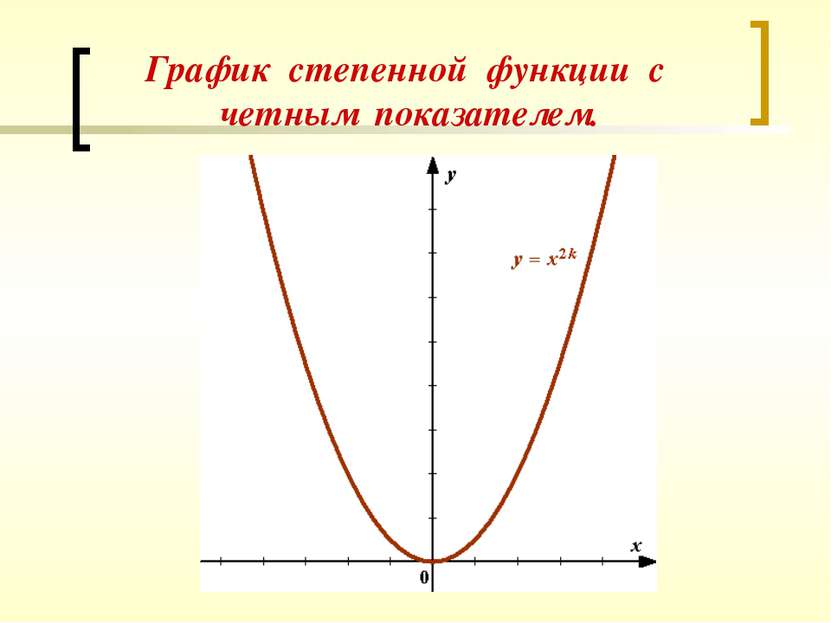
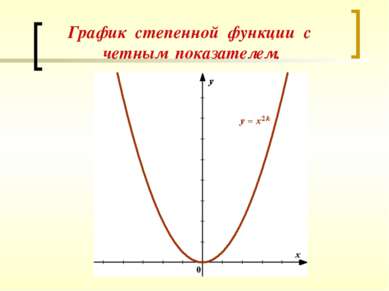
Свойства степенной функции у = х п при п = 2 k. y = х2k ; Dy = R При х = 0 у = 0. График функции проходит через начало координат. При х ≠ 0 у > 0. График функции расположен в I и II координатных четвертях. у( -х ) = ( -х )2k = х2k = у( х ) – четная. График функции симметричен относительно оси ординат. Функция возрастает в промежутке [ 0; +∞ ) и убывает в промежутке ( -∞; 0 ]. Ех = [ 0; +∞ ) Проходит ли график функции через начало координат? В каких четвертях будет расположен график функции? Определите, функция четная или нечетная. На каких промежутках функция возрастает? Убывает? Какова область значений функции?
Cлайд 7
График степенной функции с четным показателем.
Cлайд 8
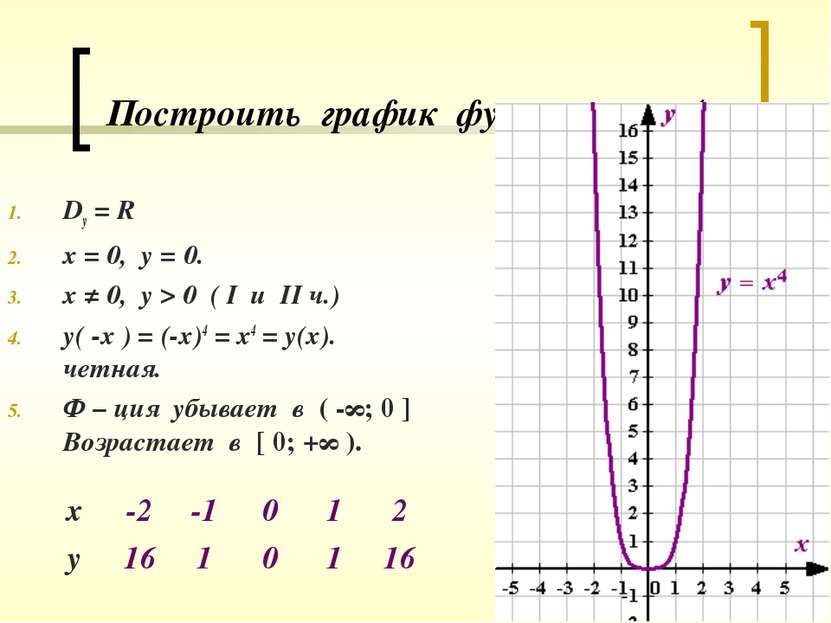
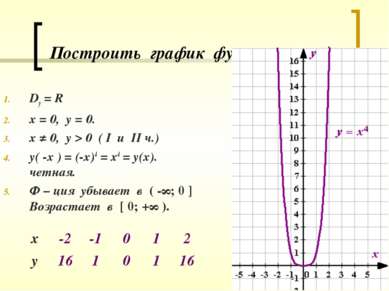Построить график функции у = х4. Dy = R х = 0, у = 0. х ≠ 0, у > 0 ( I u II ч.) у( -х ) = (-х)4 = х4 = у(х). Функция четная. Ф – ция убывает в ( -∞; 0 ] Возрастает в [ 0; +∞ ).
Cлайд 9
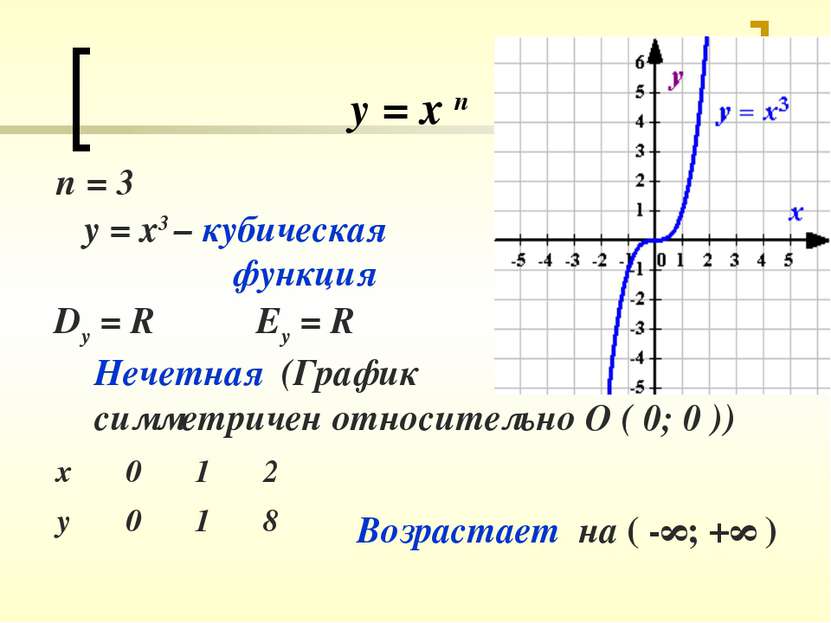
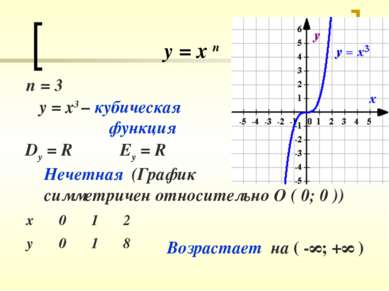у = х п n = 3 y = x3 – кубическая функция Dy = R Ey = R Нечетная (График симметричен относительно О ( 0; 0 )) Возрастает на ( -∞; +∞ )
Cлайд 10
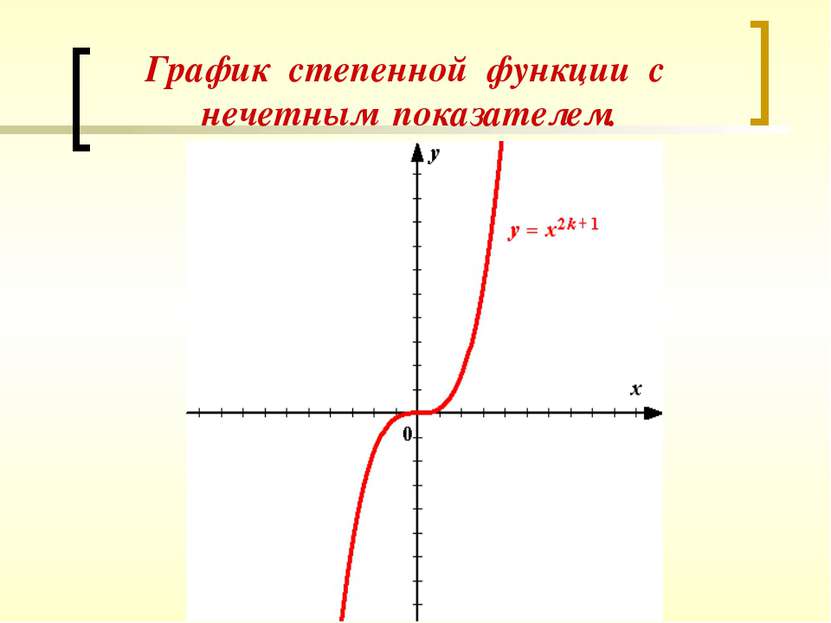
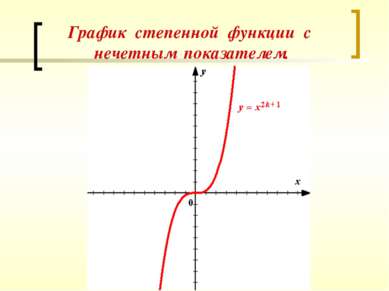
Свойства степенной функции у = х п при п = 2 k + 1. y = х2k +1; Dy= R При х = 0 у = 0. График функции проходит через начало координат. Если х > 0, то у > 0; если х < 0, то у < 0. График функции расположен в I u III координатных четвертях . у(-х) = (-х)2k+1 = -x2k+1 = -y(x). Функция нечетная. График симметричен относительно начала координат. Функция возрастает на всей области определения. Ех = R Проходит ли график функции через начало координат? В каких координатных четвертях будет расположен график функции? Определите, функция четная или нечетная. На каких промежутках функция возрастает? Убывает? Какова область значений функции?
Cлайд 11
График степенной функции с нечетным показателем.
Cлайд 12
Решение примеров: № 504 ( устно ) № 505 ( устно ) № 494 № 496 ( б, в ) № 497 ( б, в )
Cлайд 13
Домашнее задание: п.22, №№ 495; 503; 507.
Cлайд 14
Функция у = хп. II часть. Сколько корней имеет уравнение хп = 10 при п – четном? п – нечетном? Какие из графиков функций имеют центр симметрии; ось симметрии? Центр симметрии Ось симметрии
Cлайд 15
Сравните: f ( x ) = x10 f ( x ) = x9 a) б) в) г) а) б) в) г) < < = > > > < <
Cлайд 16
Найдите ошибку: 1. 2. 3.
Cлайд 17
Решите уравнения: 1. 2. 3. 4. 5. Ответ: Ответ: Ответ: Ответ: Ответ: Корней нет
Cлайд 18
Самостоятельная работа: I вариант. II вариант.
Cлайд 19
До новых встреч!
