X
Код презентации скопируйте его
Свойства пирамиды с равными боковыми ребрами
Скачать эту презентацию
Презентация на тему Свойства пирамиды с равными боковыми ребрами
Скачать эту презентациюCлайд 1
«Свойства пирамиды с равными боковыми ребрами» Должикова Наталья Юрьевна
Cлайд 2
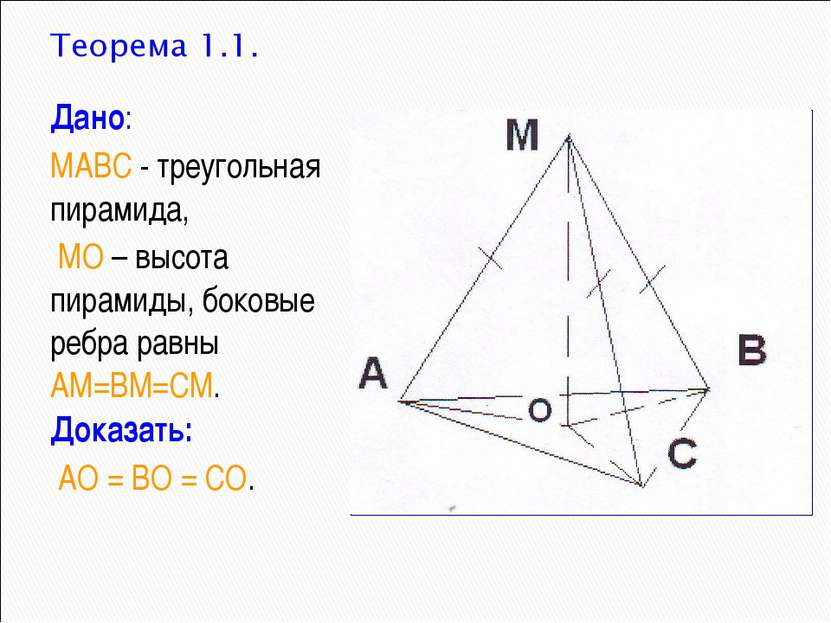
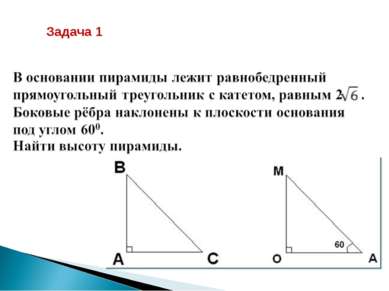
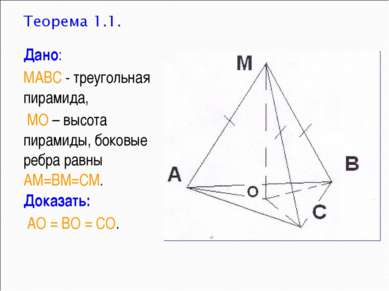Дано: МАВС - треугольная пирамида, МО – высота пирамиды, боковые ребра равны АМ=ВМ=СМ. Доказать: АО = ВО = СО.
Cлайд 3
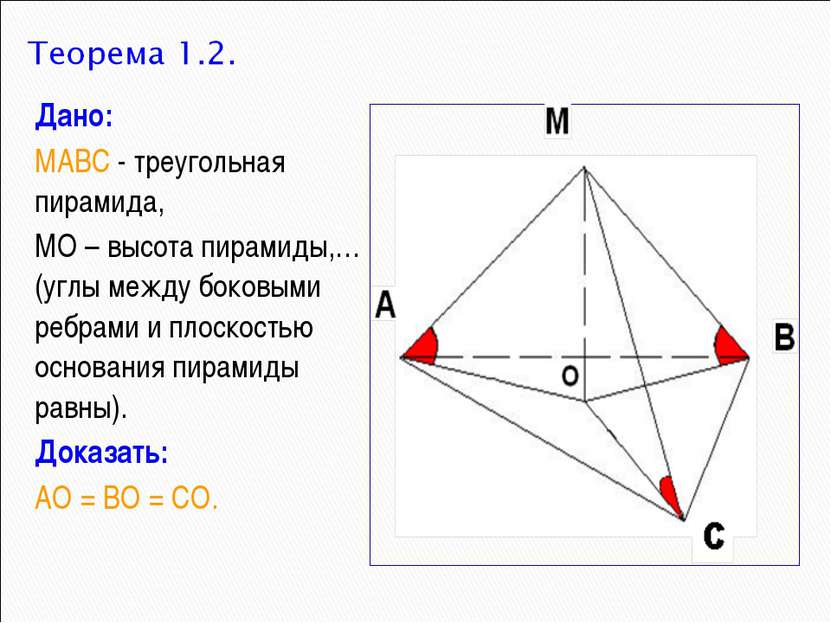
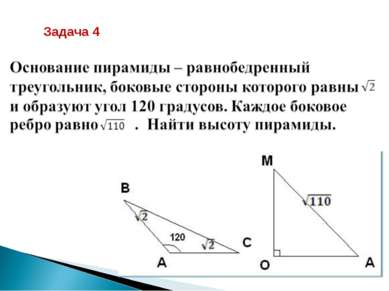
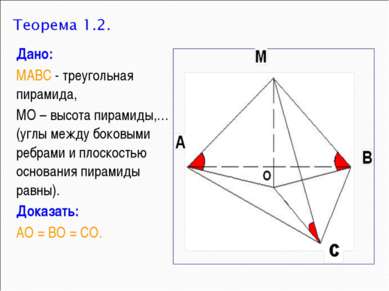Дано: МАВС - треугольная пирамида, МО – высота пирамиды,…(углы между боковыми ребрами и плоскостью основания пирамиды равны). Доказать: АО = ВО = СО.
Cлайд 4
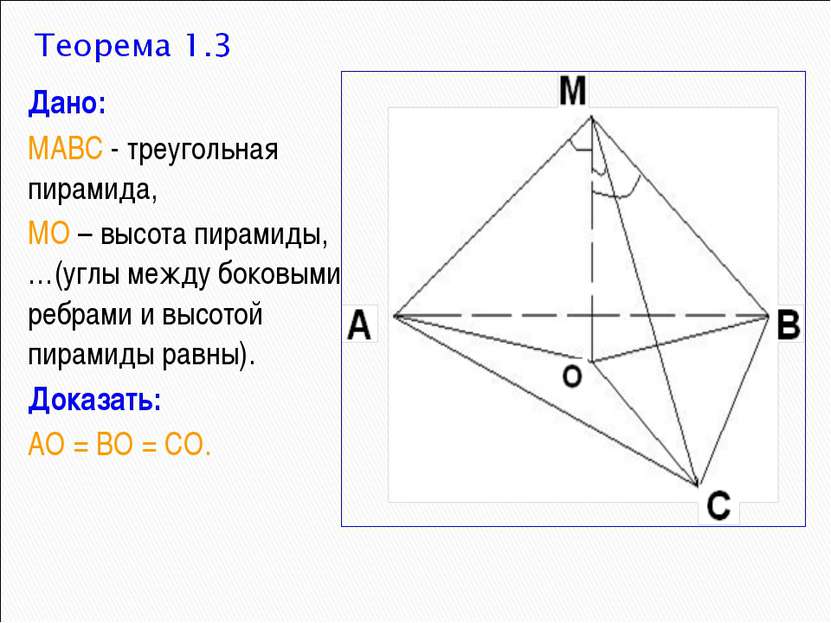
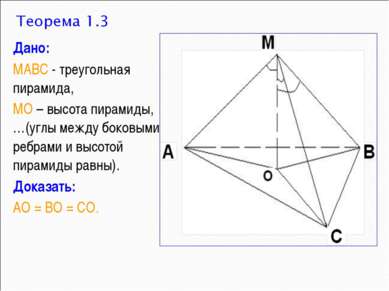Дано: МАВС - треугольная пирамида, МО – высота пирамиды, …(углы между боковыми ребрами и высотой пирамиды равны). Доказать: АО = ВО = СО.
Cлайд 5
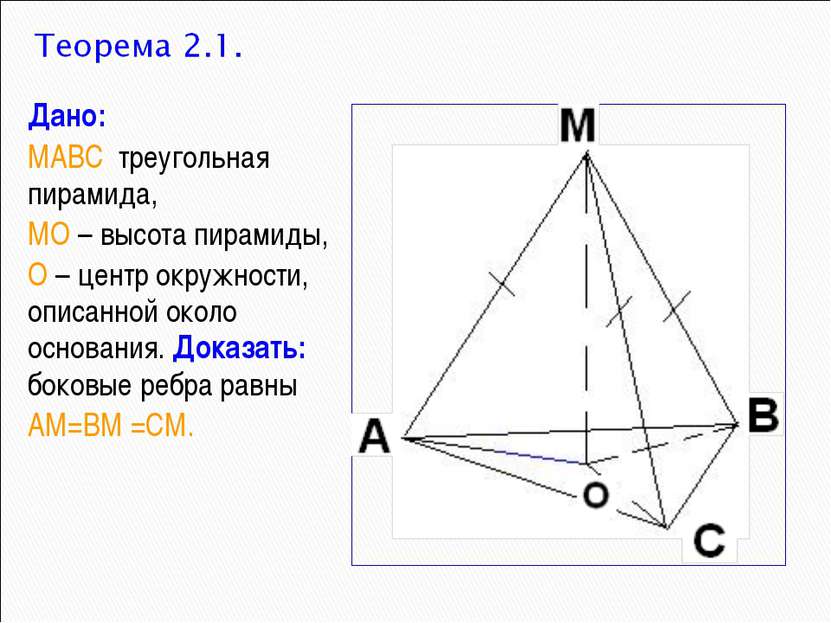
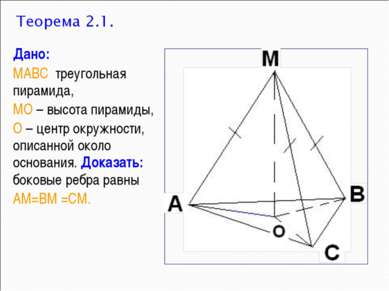Дано: МАВС треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной около основания. Доказать: боковые ребра равны АМ=ВМ =СМ.
Cлайд 6
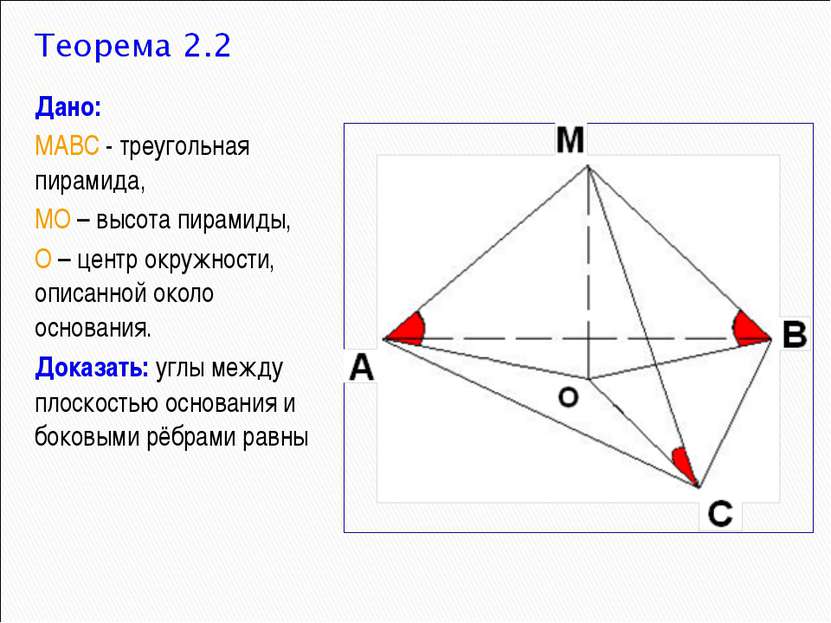
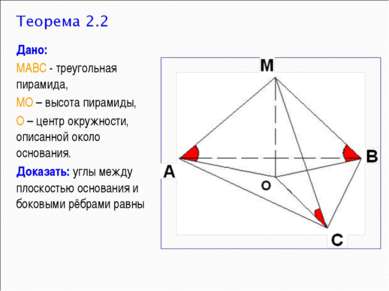Дано: МАВС - треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной около основания. Доказать: углы между плоскостью основания и боковыми рёбрами равны
Cлайд 7
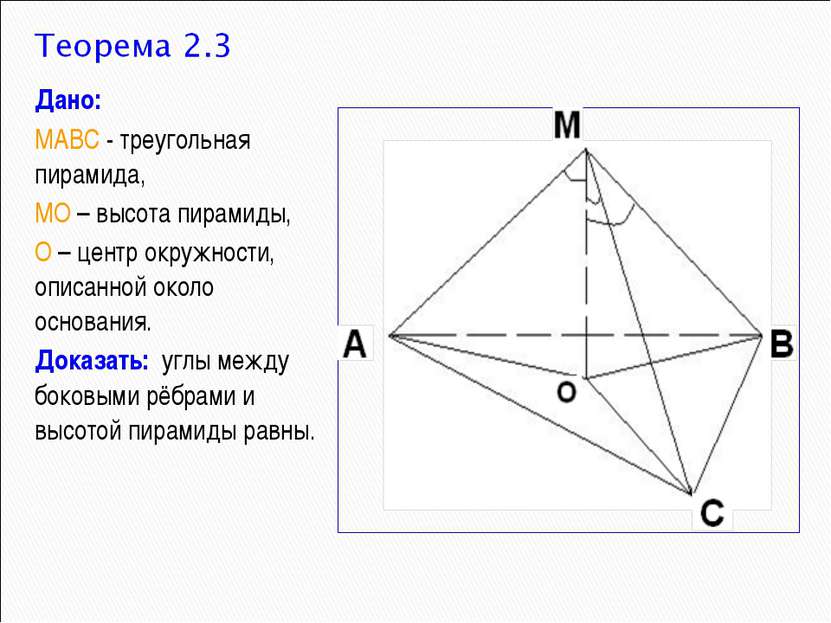
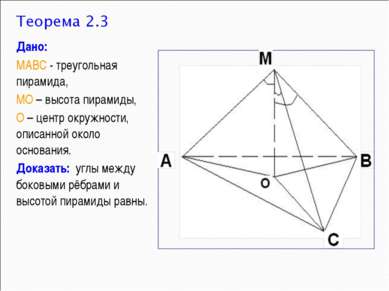Дано: МАВС - треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной около основания. Доказать: углы между боковыми рёбрами и высотой пирамиды равны.
Cлайд 8
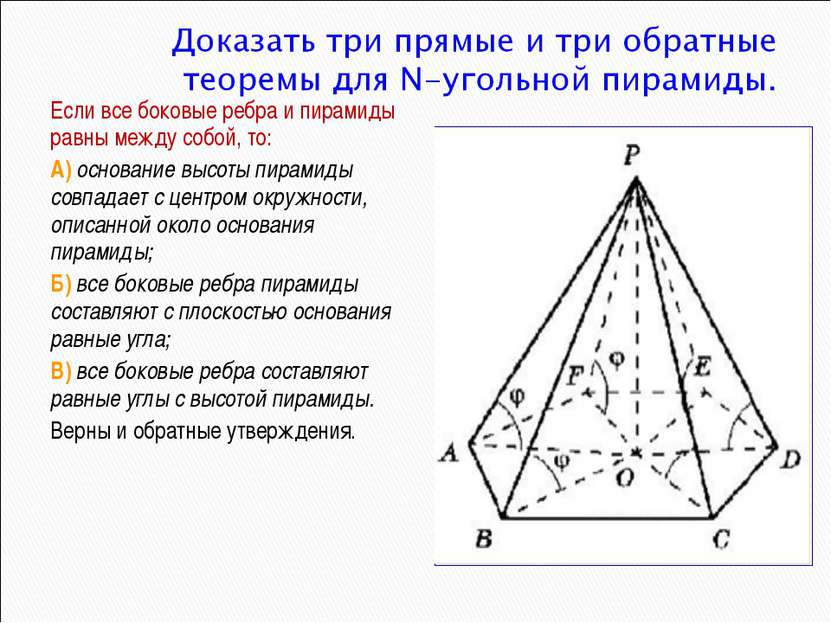
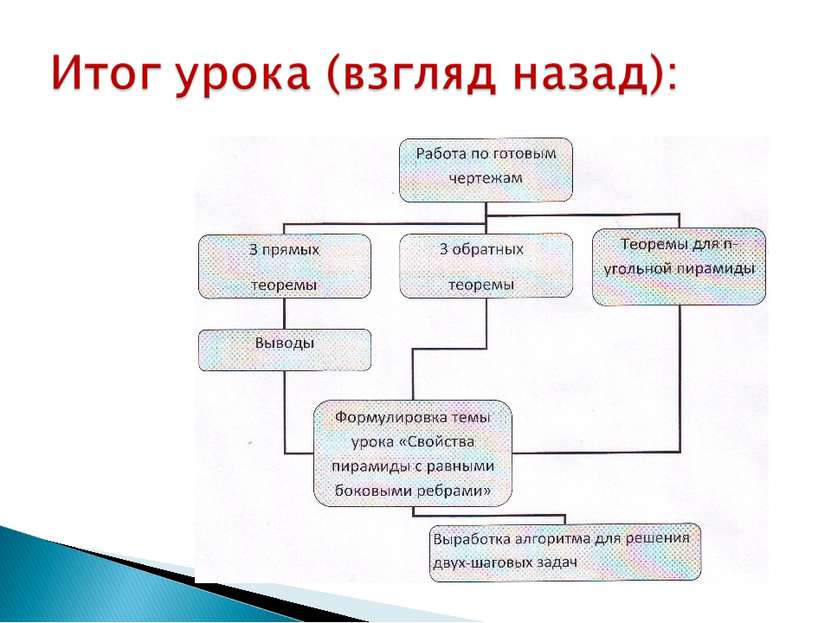
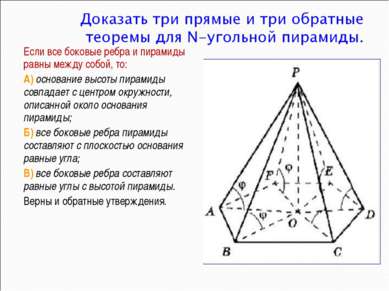Если все боковые ребра и пирамиды равны между собой, то: А) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; Б) все боковые ребра пирамиды составляют с плоскостью основания равные угла; В) все боковые ребра составляют равные углы с высотой пирамиды. Верны и обратные утверждения.
Cлайд 9
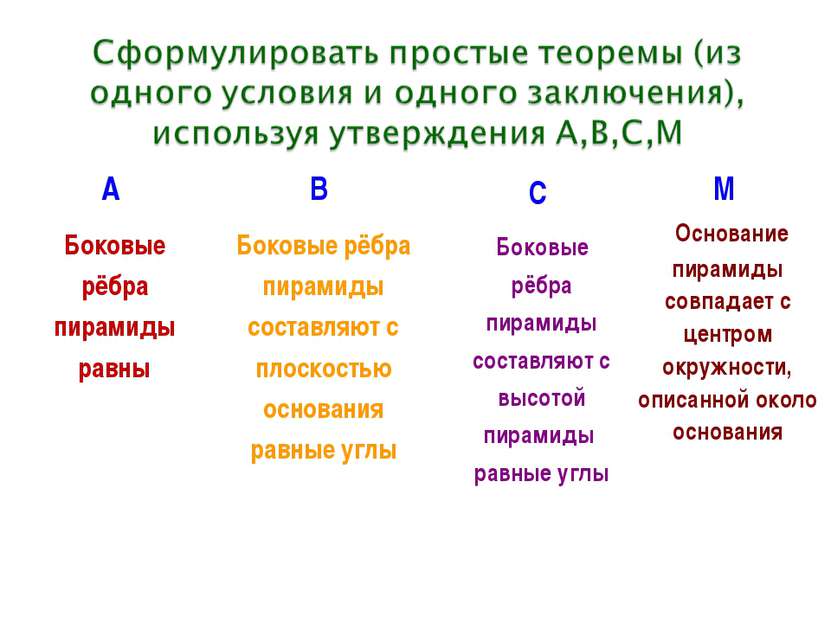
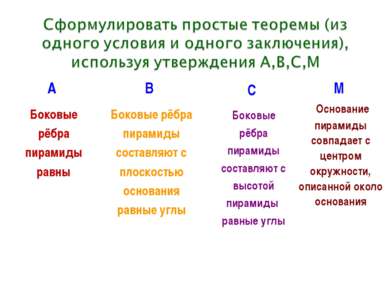А Боковые рёбра пирамиды равны В Боковые рёбра пирамиды составляют с плоскостью основания равные углы С Боковые рёбра пирамиды составляют с высотой пирамиды равные углы М Основание пирамиды совпадает с центром окружности, описанной около основания
Cлайд 10
1.Наличие в условии задачи одного из условий (А,В,С,). Из этих условий вытекает М. 2. Решить основание (найти радиус окружности, описанной около основания). 3. Решить прямоугольный треугольник, например, МОА.
Cлайд 11
Задача 1
Cлайд 12
Задача 2
Cлайд 13
Задача 3
Cлайд 14
Задача 4
Cлайд 15
Cлайд 16
