X
Код презентации скопируйте его
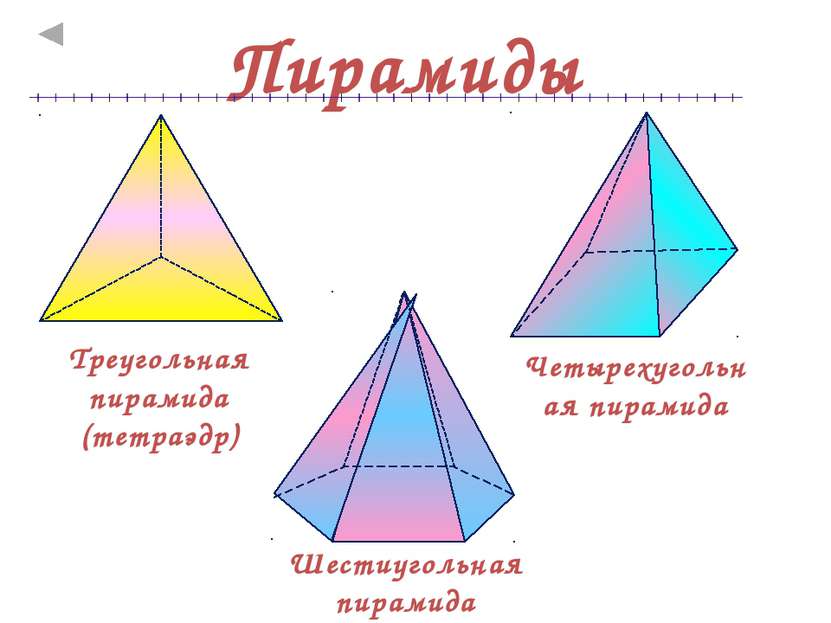
Пирамиды
Скачать эту презентацию
Презентация на тему Пирамиды
Скачать эту презентациюCлайд 1
История появления Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был Демокрит а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
Cлайд 2
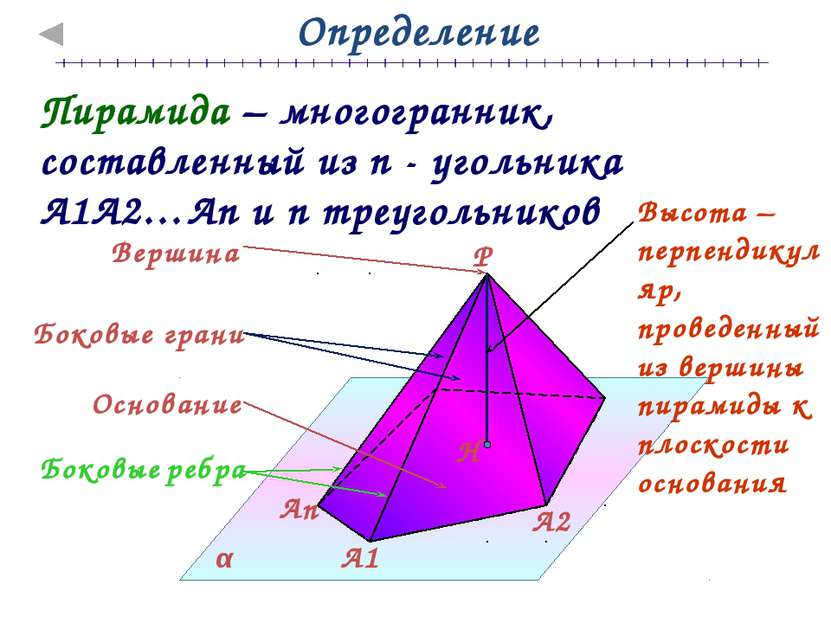
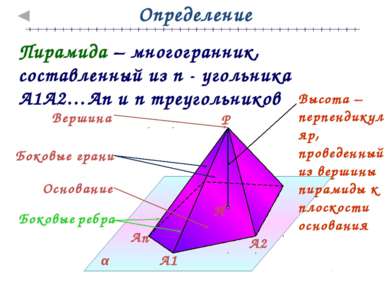
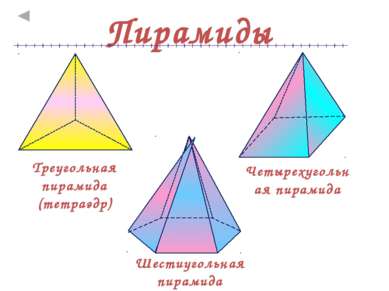
Определение Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости основания Боковые ребра Основание Боковые грани Вершина
Cлайд 3
Пирамиды Треугольная пирамида (тетраэдр) Шестиугольная пирамида Четырехугольная пирамида
Cлайд 4
Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.
Cлайд 5
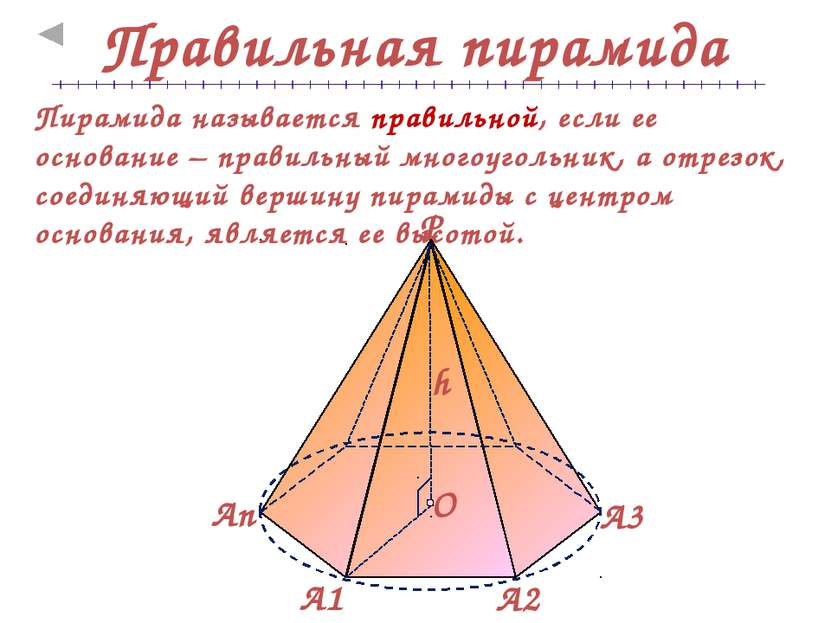
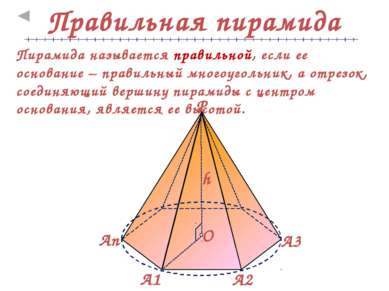
Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. А3
Cлайд 6
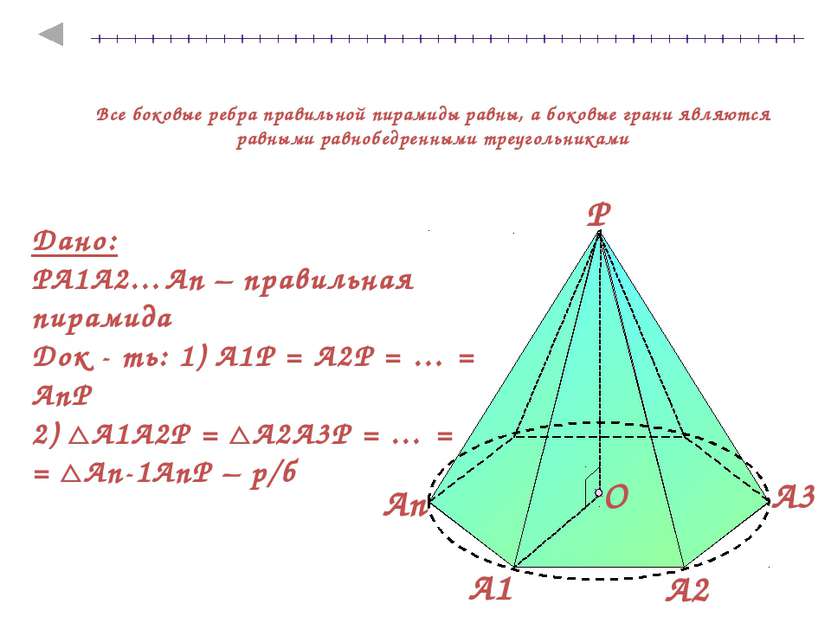
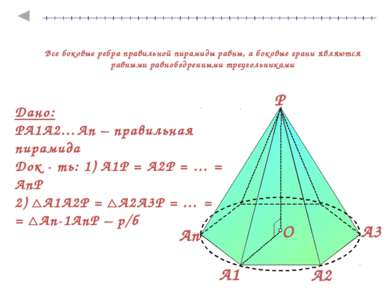
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками Дано: PA1A2…An – правильная пирамида Док - ть: 1) А1Р = А2Р = … = АnР 2) А1А2Р = А2А3Р = … = = Аn-1АnР – р/б А3
Cлайд 7
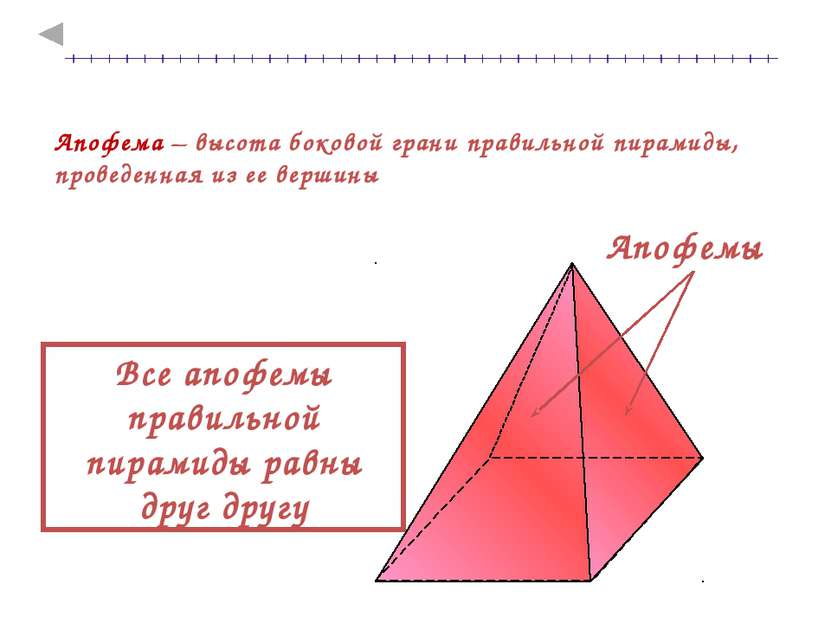
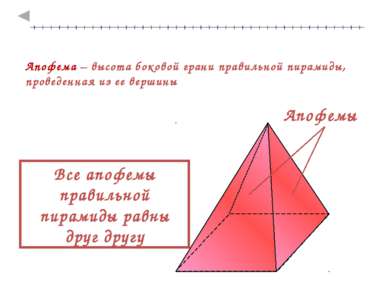
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Все апофемы правильной пирамиды равны друг другу Апофемы
Cлайд 8
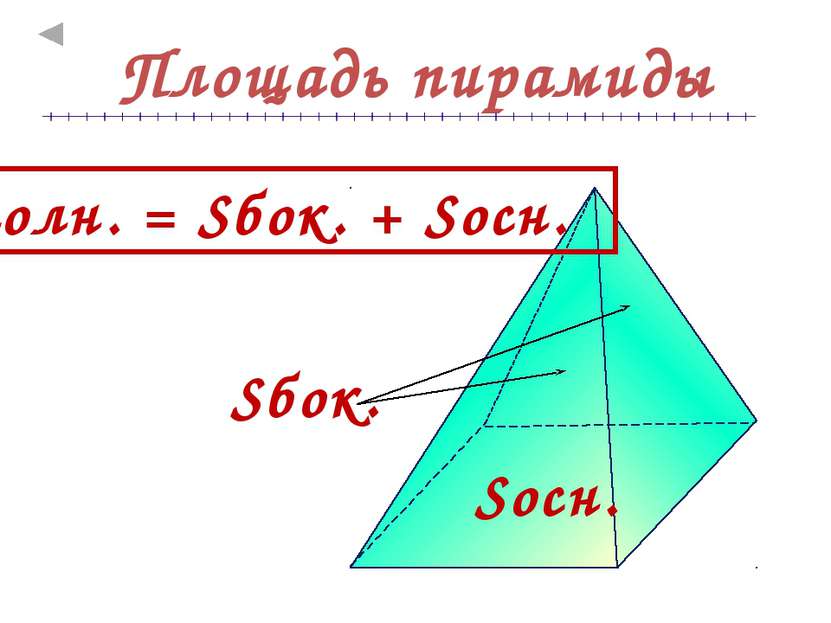
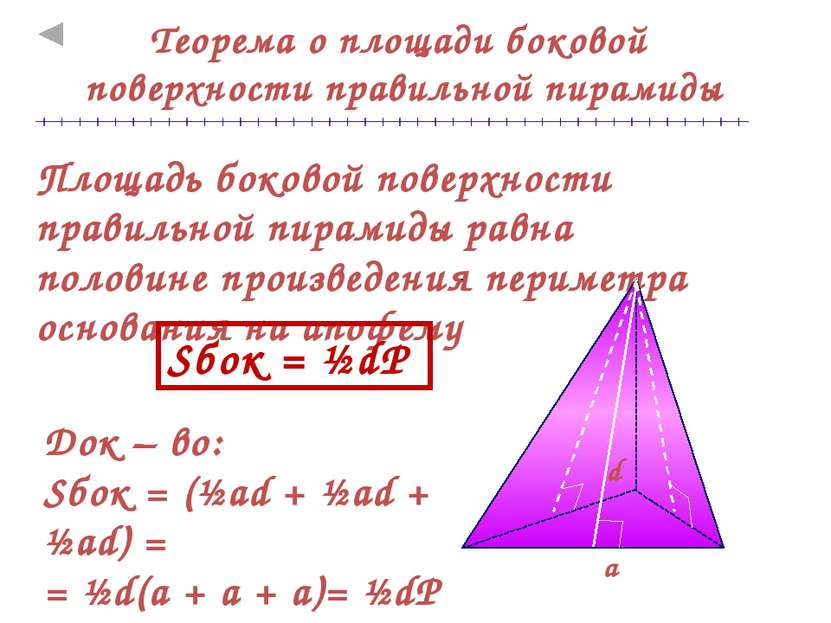
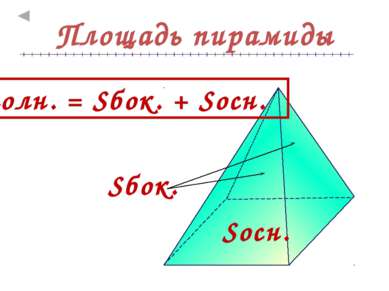
Теорема о площади боковой поверхности правильной пирамиды Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему Док – во: Sбок = (½ad + ½ad + ½ad) = = ½d(a + a + a)= ½dP Sбок = ½dP a
Cлайд 9
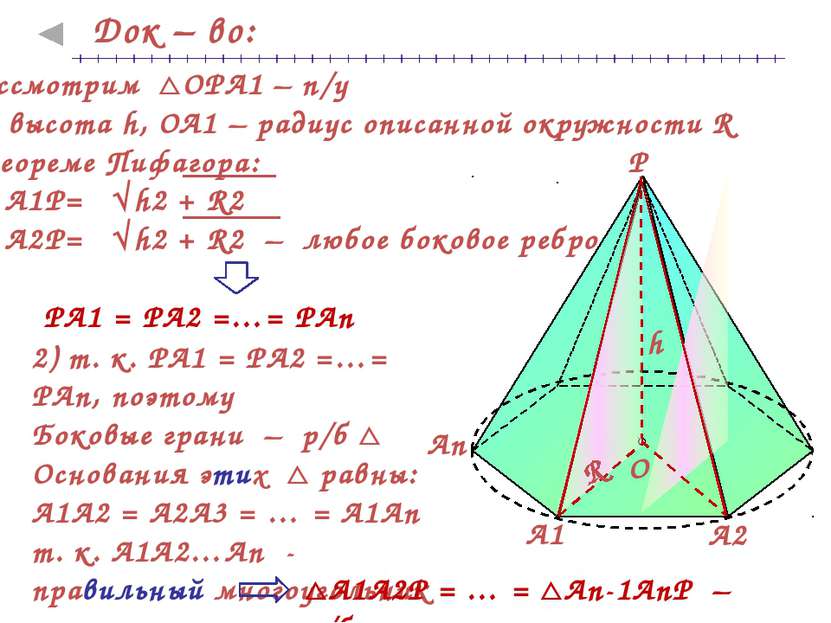
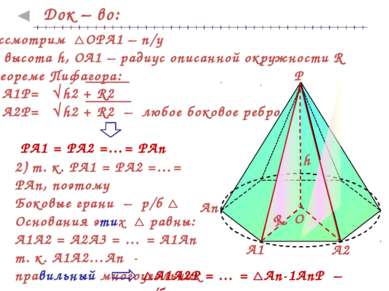Док – во: 2) т. к. РА1 = РА2 =…= РАn, поэтому Боковые грани – р/б Основания этих равны: А1А2 = А2А3 = … = А1Аn т. к. А1А2…Аn - правильный многоугольник А1А2Р = … = Аn-1АnР – р/б Рассмотрим ОРА1 – п/у РО – высота h, OA1 – радиус описанной окружности R По теореме Пифагора: A1P= h2 + R2 A2P= h2 + R2 – любое боковое ребро РА1 = РА2 =…= РАn А1 А2 Аn Р О R h
Cлайд 10
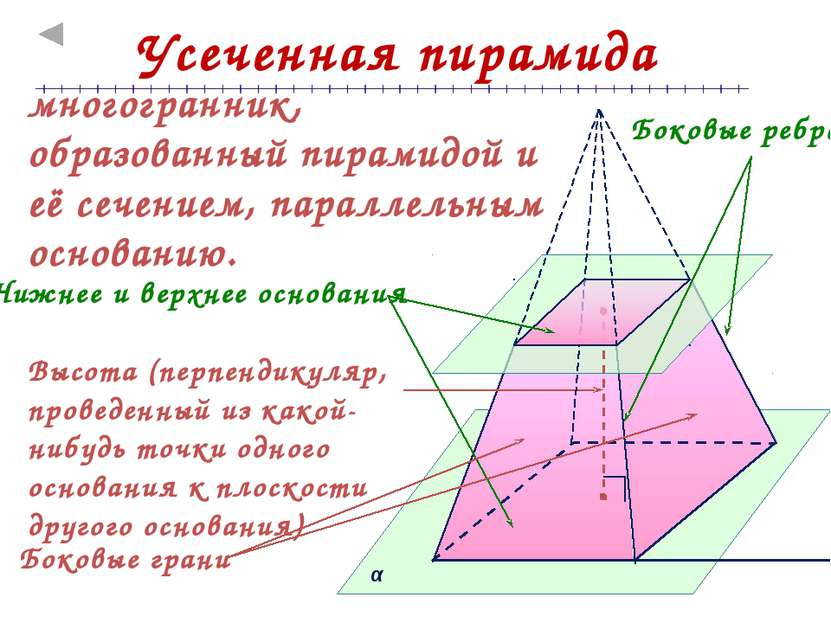
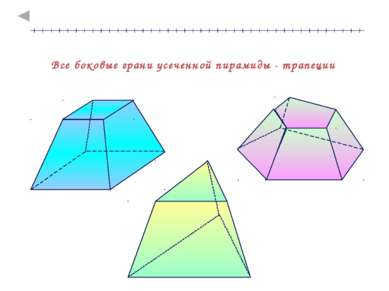
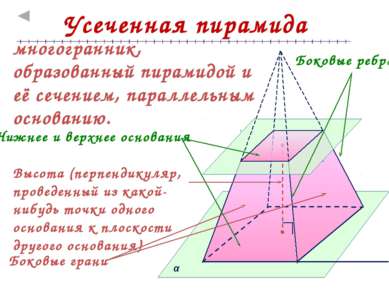
Усеченная пирамида многогранник, образованный пирамидой и её сечением, параллельным основанию. Нижнее и верхнее основания Боковые грани Боковые ребра Высота (перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания) α
Cлайд 11
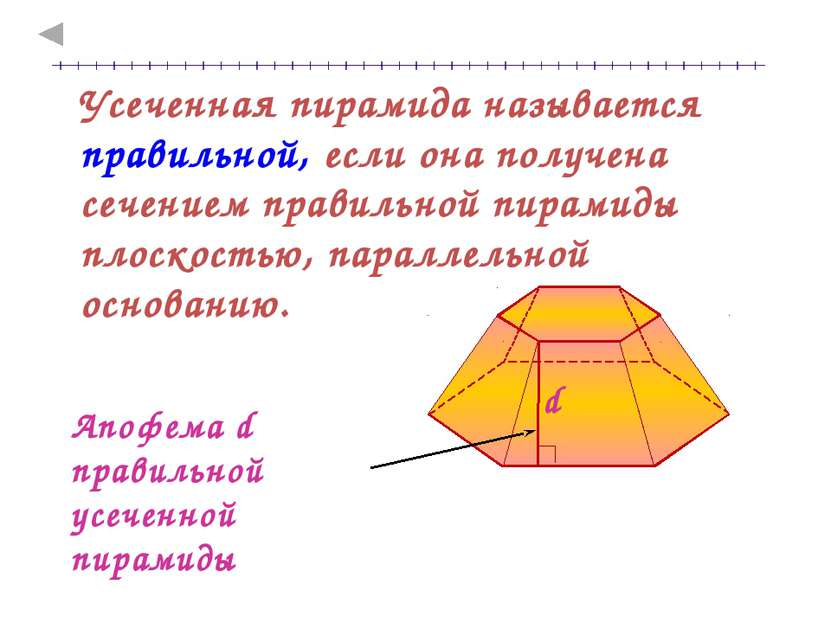
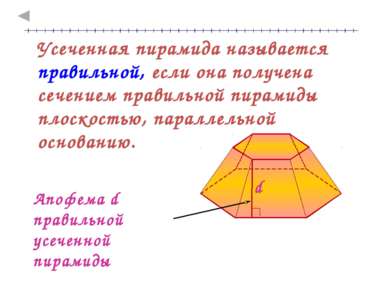
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Апофема d правильной усеченной пирамиды d
Cлайд 12
Теорема о площади боковой поверхности правильной усеченной пирамиды Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему S бок = ½(Р1 + Р2) d P1= 4a1 P2= 4a2 Док – во: S бок = ½d(a1+a2) + ½d(a1+a2) + + ½ d(a1+a2) + ½d(a1+a2) = = ½d(a1+ a2+ a1+ a2+ a1+ a2+ a1+ a2) = = ½d(4a1+ 4a2) = ½d(P1+ P2) a1 d
Cлайд 13
Все боковые грани усеченной пирамиды - трапеции
Cлайд 14
Cлайд 15
