X
Код презентации скопируйте его
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Скачать эту презентацию
Презентация на тему Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Скачать эту презентациюCлайд 1
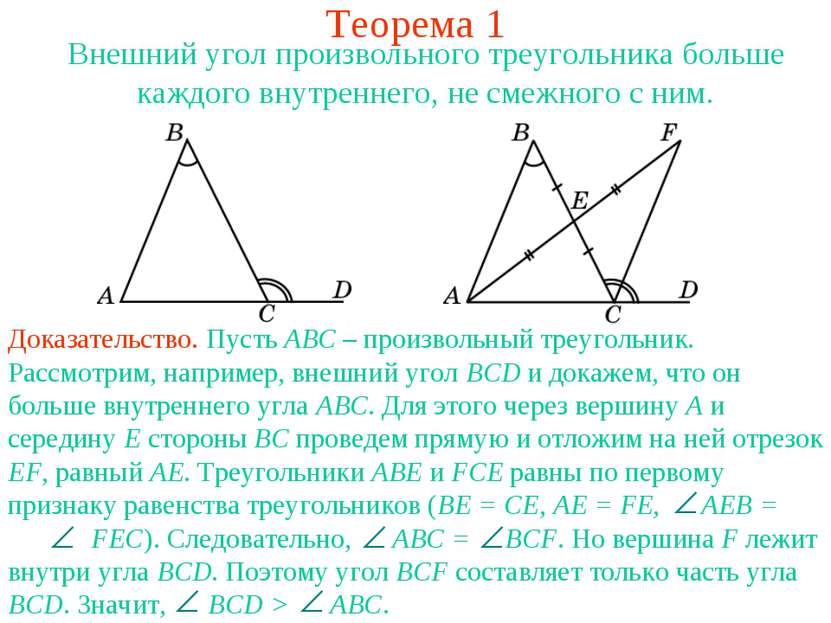
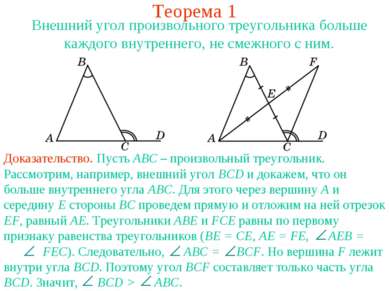Теорема 1 Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним.
Cлайд 2
Теорема 2 В произвольном треугольнике против большей стороны лежит больший угол.
Cлайд 3
Упражнение 1 Может ли внешний угол треугольника равняться его внутреннему углу? Ответ: Да, в прямоугольном треугольнике.
Cлайд 4
Упражнение 2 Может ли внешний угол треугольника быть меньше его внутреннего угла? Ответ: Да, в тупоугольном треугольнике.
Cлайд 5
Упражнение 3 Сколько в треугольнике может быть: а) прямых углов; б) тупых углов? Ответ: а), б) Один.
Cлайд 6
Упражнение 4 Известно, что в треугольнике ABC BC > AC >AB. Какой из углов больше: а) B или A; б) C или A; в) B или С? Ответ: а), б) A; в) B.
Cлайд 7
Упражнение 5 В треугольнике ABC сторона AB наибольшая. Какие углы этого треугольника острые? Каким может быть угол C? Ответ: Углы A и B острые. Угол C может быть острым, прямым или тупым.
Cлайд 8
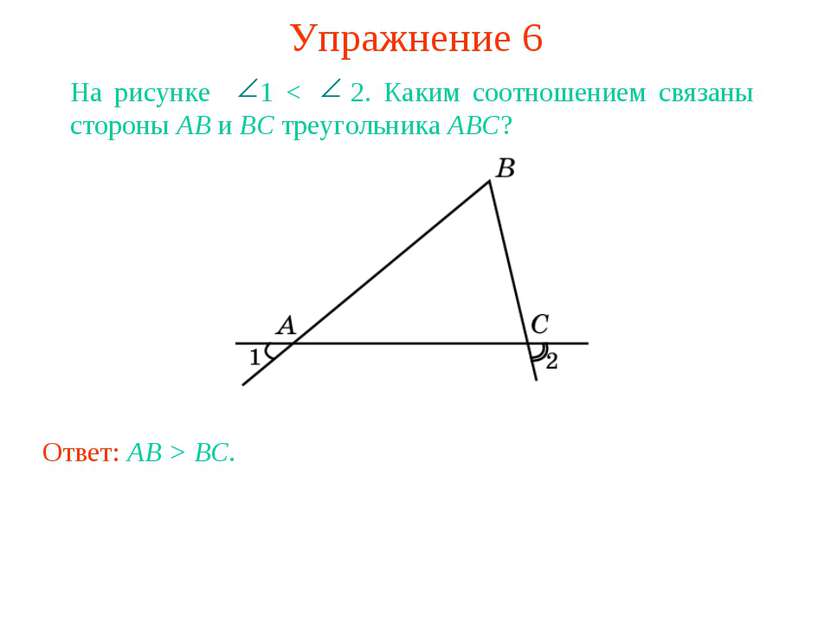
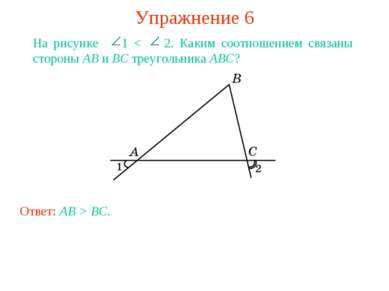Упражнение 6 На рисунке 1 < 2. Каким соотношением связаны стороны AB и BC треугольника ABC? Ответ: AB > BC.
Cлайд 9
Упражнение 7 Верно ли, что в произвольном треугольнике против большего угла лежит большая сторона? Ответ: Да.
Cлайд 10
Упражнение 8 Ответ: а) BC > AC > AB; б) BC > AB, AC = AB.
Cлайд 11
Упражнение 9 На рисунке DE
Cлайд 12
Упражнение 10 Какой вид имеет треугольник, если: а) два его угла равны; б) три его угла равны? Ответ: а) Равнобедренный; б) правильный.
Cлайд 13
Упражнение 11 Точка M лежит внутри треугольника ABC. Какой из углов больше BAC или BMC? Ответ: BMC.
Cлайд 14
Упражнение 12 В треугольнике ABC выполняется неравенство AC > BC, CD – медиана. Какой из углов больше ACD или BCD? Ответ: BCD.
