X
Код презентации скопируйте его
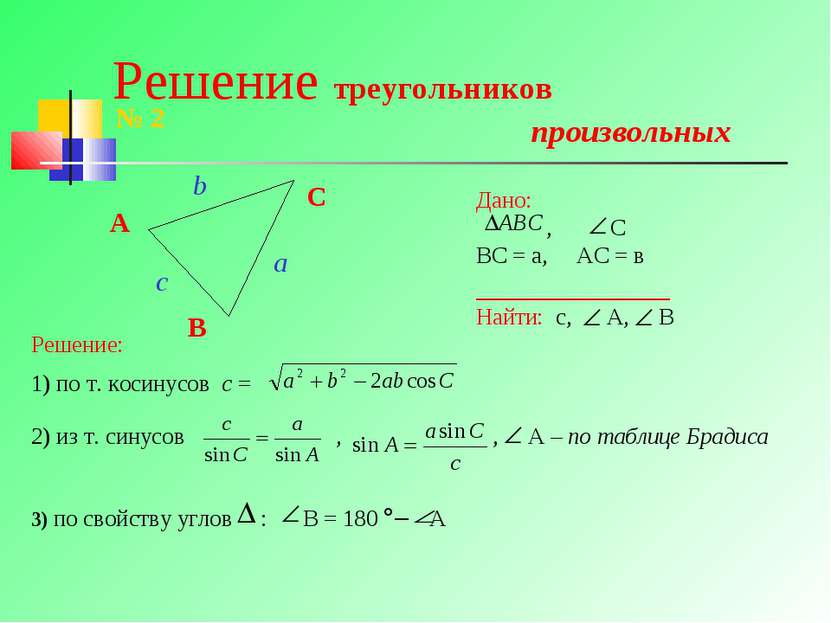
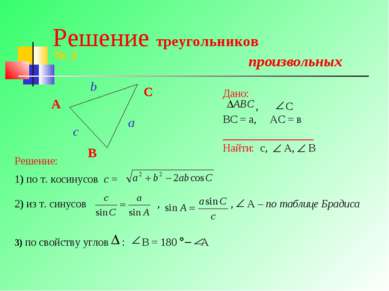
Соотношения между сторонами и углами в треугольнике
Скачать эту презентацию
Презентация на тему Соотношения между сторонами и углами в треугольнике
Скачать эту презентациюCлайд 1
Геометрия, 9 класс УЗ: «Соотношения между сторонами и углами в треугольнике» 1. Дайте определение sin α, cos α 2. Как изменяется: sin α, cos α?
Cлайд 2
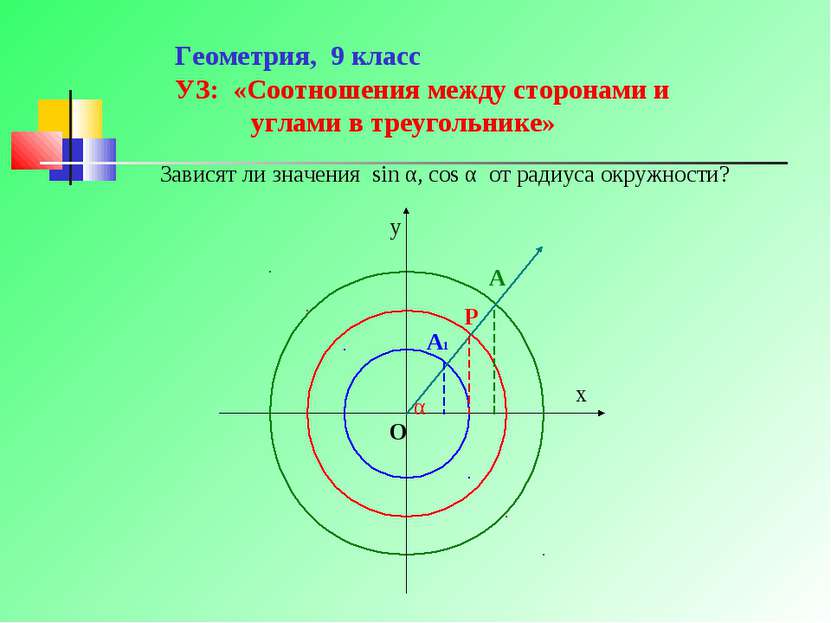
Геометрия, 9 класс УЗ: «Соотношения между сторонами и углами в треугольнике» Зависят ли значения sin α, cos α от радиуса окружности?
Cлайд 3
Геометрия, 9 класс УЗ: «Соотношения между сторонами и углами в треугольнике» уз 1: координаты точки A (OA cos C; OA sin C) y
Cлайд 4
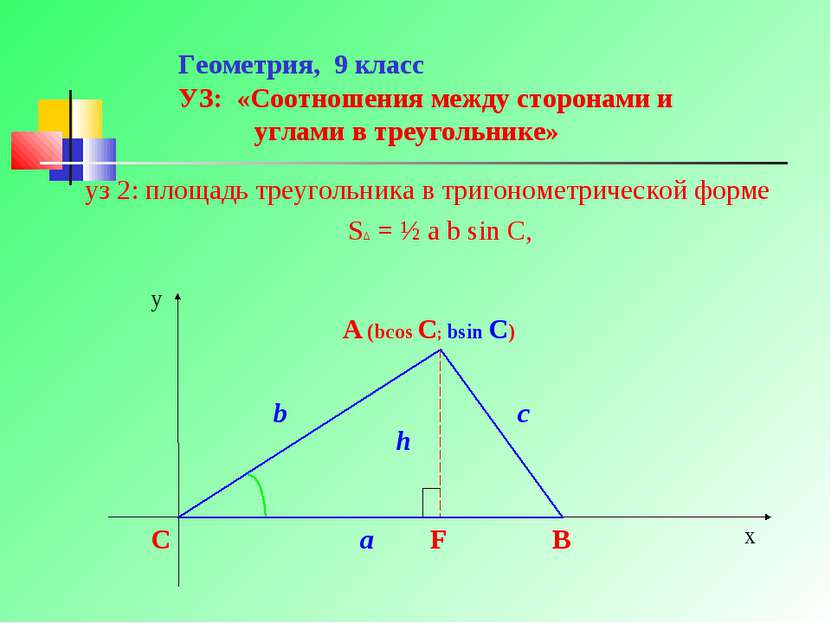
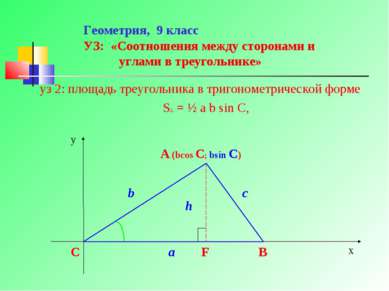Геометрия, 9 класс УЗ: «Соотношения между сторонами и углами в треугольнике» уз 2: площадь треугольника в тригонометрической форме S∆ = ½ a b sin C,
Cлайд 5
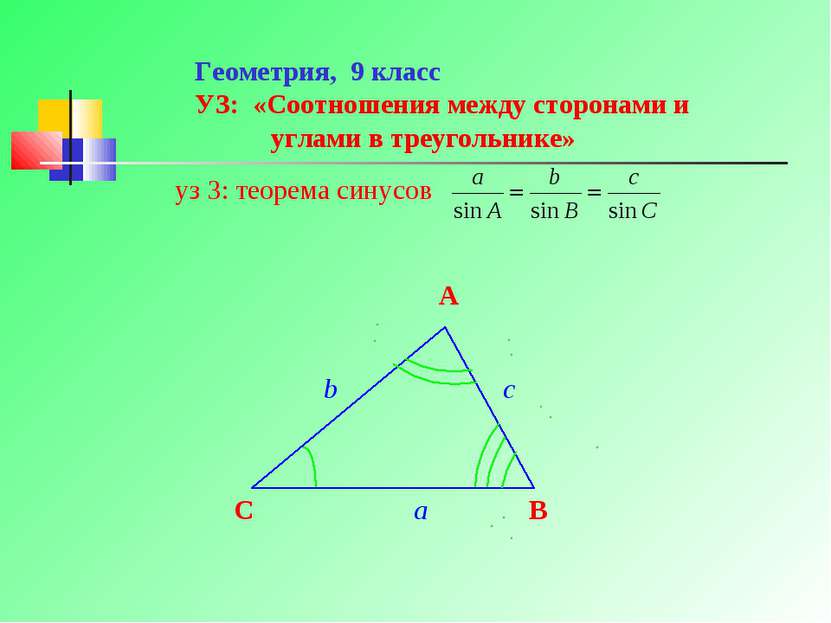
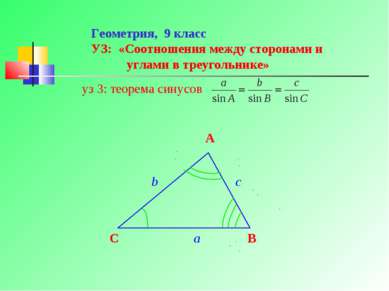Геометрия, 9 класс УЗ: «Соотношения между сторонами и углами в треугольнике» уз 3: теорема синусов
Cлайд 6
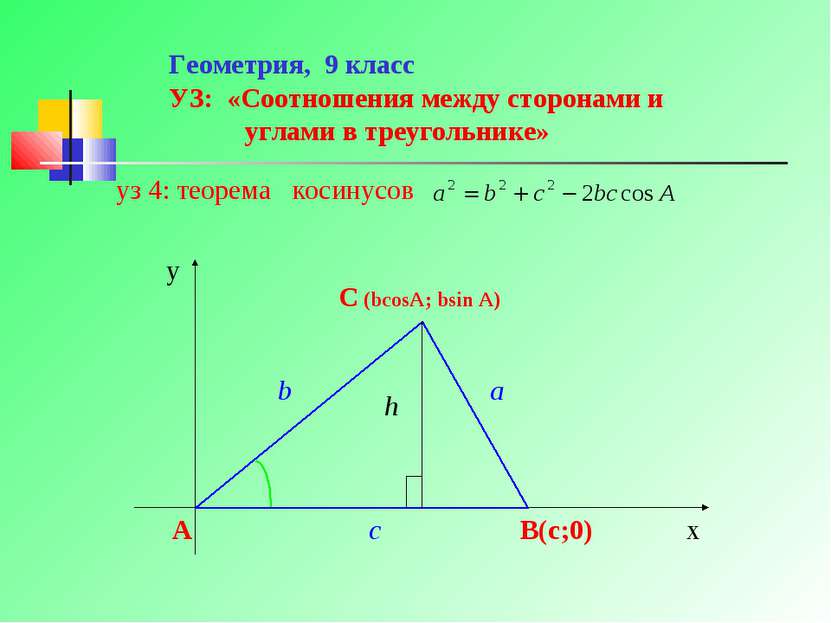
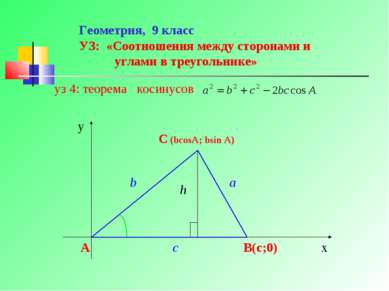Геометрия, 9 класс УЗ: «Соотношения между сторонами и углами в треугольнике» уз 4: теорема косинусов у
Cлайд 7
Решение треугольников прямоугольных Решение: 1) по т. Пифагора: с = 2) по определению sin А = , А – по таблице Брадиса 3) по свойству острых углов прямоугольного : В = 90 – А В С Дано: , С = 90, ВС = а, АС = в _______________ Найти: с, А, В с № 1 а в А
Cлайд 8
Решение треугольников произвольных A B C № 2 Дано: , С ВС = а, АС = в ______________ Найти: с, А, В a c b Решение: 1) по т. косинусов с = 2) из т. синусов , , А – по таблице Брадиса 3) по свойству углов : В = 180 °– А
