X
Код презентации скопируйте его
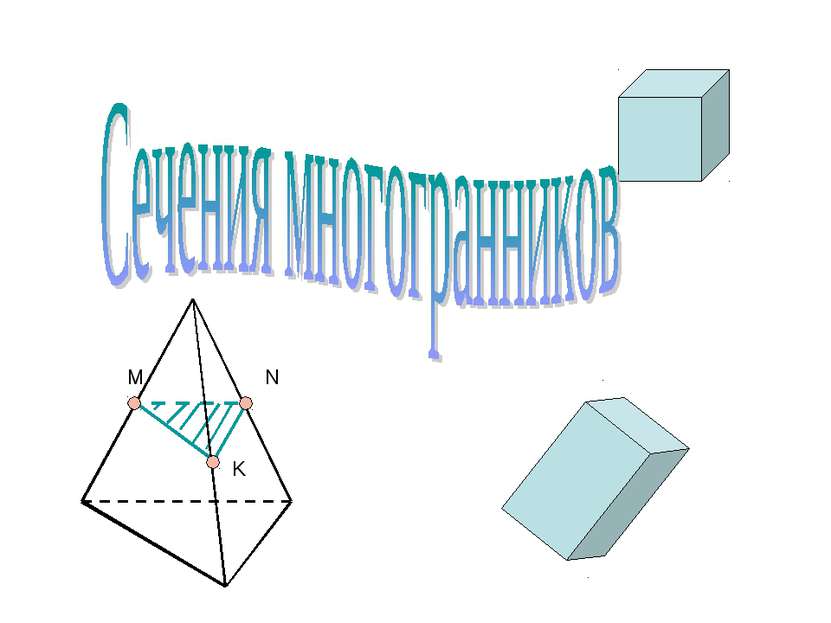
Сечения многогранников
Скачать эту презентацию
Презентация на тему Сечения многогранников
Скачать эту презентациюCлайд 1
M N K
Cлайд 2
Цели: формировать навыки решения задач на построение сечения многогранника; развивать пространственное воображение
Cлайд 3
Содержание Демонстрация построения сечений Задача № 1 Задача № 2 Задача № 3 Задача № 4 Задача № 5 Задачи для самостоятельного решения Задача № 6 Задача № 7 Задача № 8 Задача № 9 Проверка правильности решения задач Задача № 6 Задача № 7 Задача № 8 Задача № 9
Cлайд 4
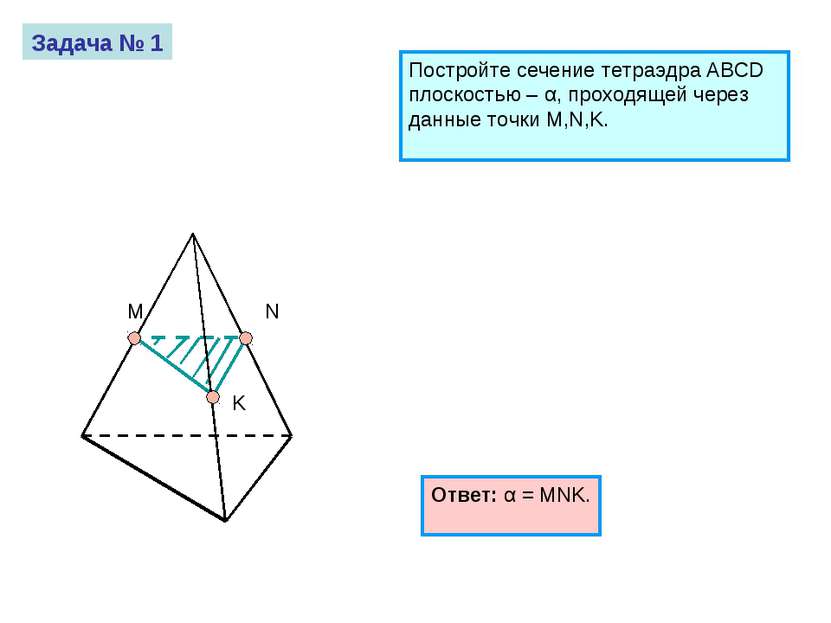
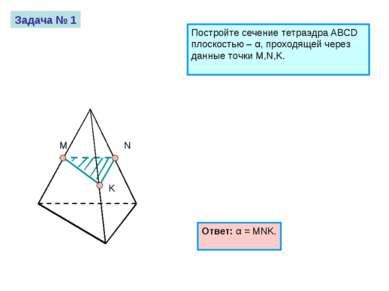M N K Задача № 1 Постройте сечение тетраэдра ABCD плоскостью – α, проходящей через данные точки M,N,K. Ответ: α = MNK.
Cлайд 5
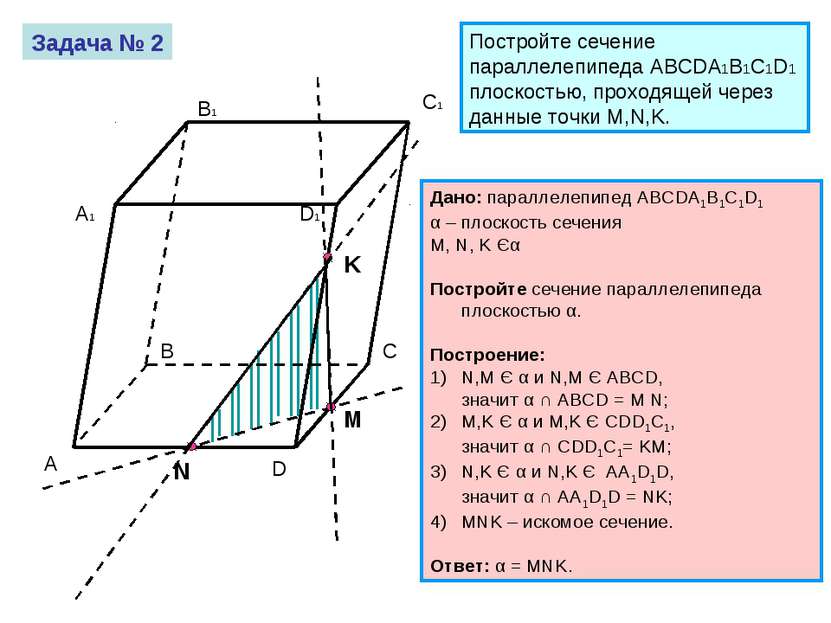
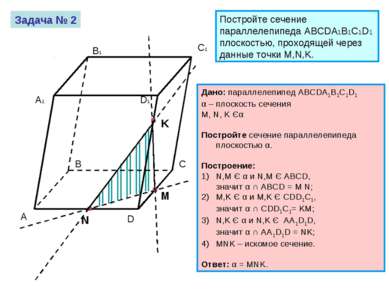Задача № 2 Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через данные точки M,N,K. А B C D A1 B1 C1 D1 Дано: параллелепипед ABCDA1B1C1D1 α – плоскость сечения M, N, K Єα Постройте сечение параллелепипеда плоскостью α. Построение: N,M Є α и N,M Є ABCD, значит α ∩ ABCD = M N; M,K Є α и M,K Є CDD1C1, значит α ∩ CDD1C1= KM; N,K Є α и N,K Є AA1D1D, значит α ∩ AA1D1D = NK; MNK – искомое сечение. Ответ: α = MNK.
Cлайд 6
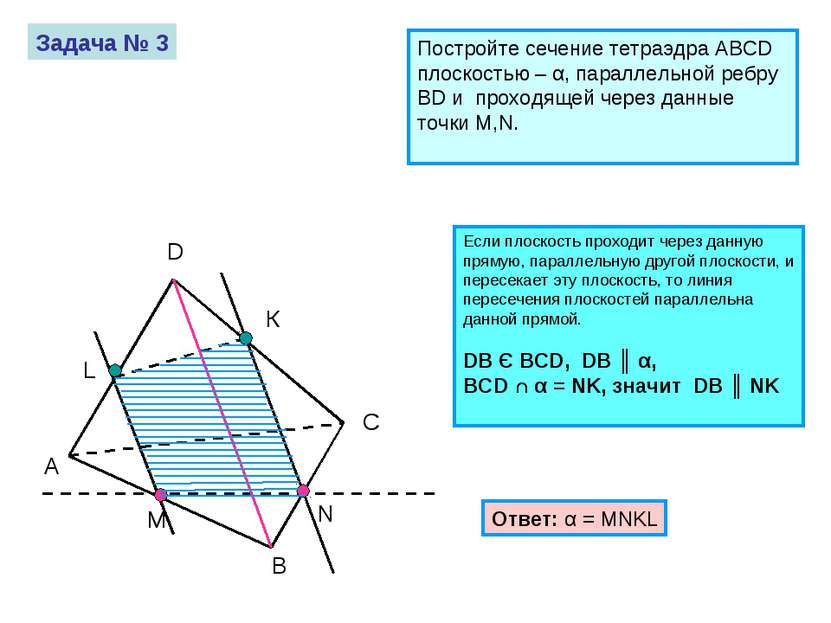
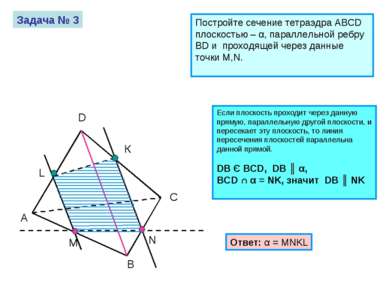Задача № 3 Постройте сечение тетраэдра ABCD плоскостью – α, параллельной ребру BD и проходящей через данные точки M,N. A B C D M N Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. DB Є BCD, DB ║ α, BCD ∩ α = NK, значит DB ║ NK Ответ: α = MNKL
Cлайд 7
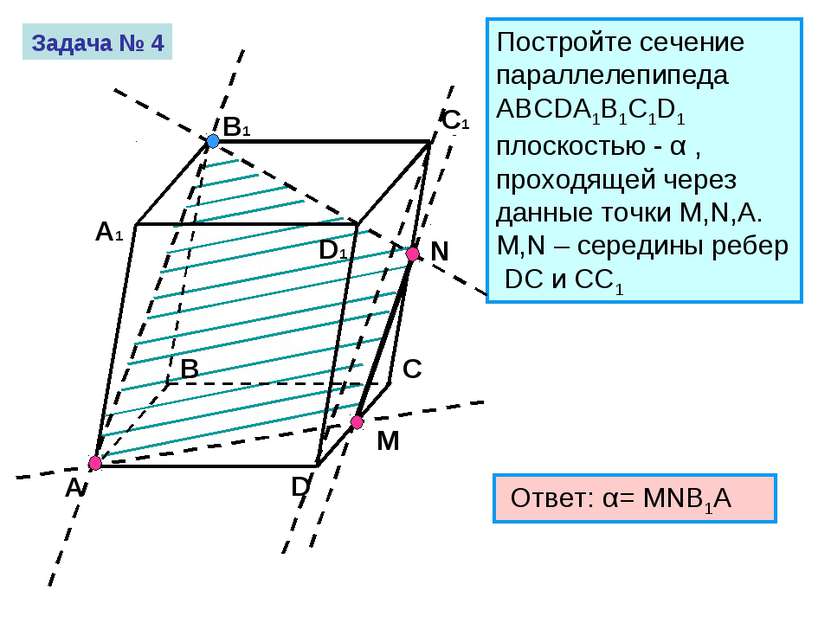
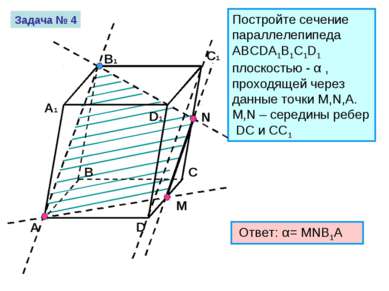Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью - α , проходящей через данные точки M,N,А. M,N – середины ребер DC и CC1 Ответ: α= MNB1A Задача № 4
Cлайд 8
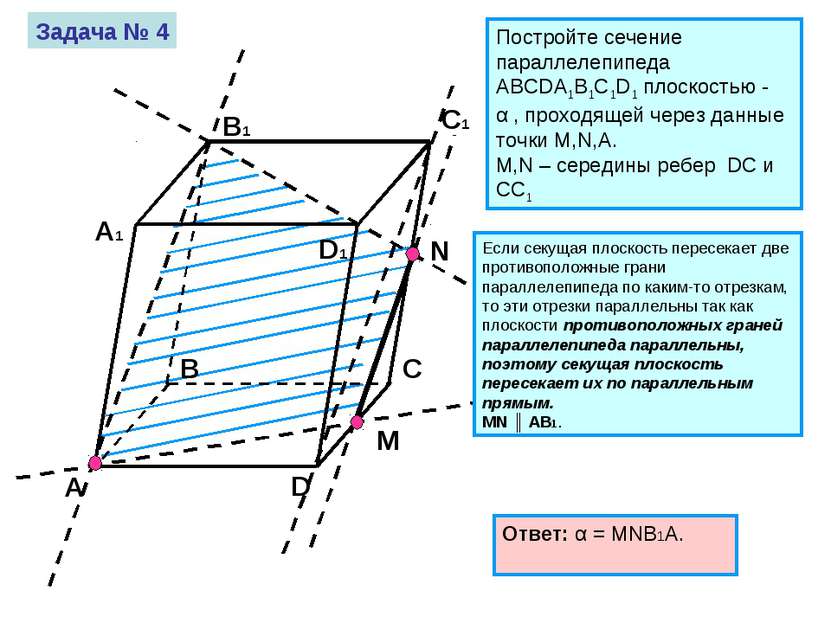
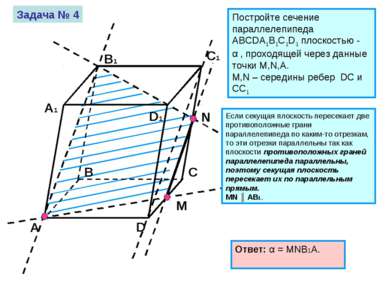Задача № 4 Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью - α , проходящей через данные точки M,N,А. M,N – середины ребер DC и CC1 Если секущая плоскость пересекает две противоположные грани параллелепипеда по каким-то отрезкам, то эти отрезки параллельны так как плоскости противоположных граней параллелепипеда параллельны, поэтому секущая плоскость пересекает их по параллельным прямым. MN ║ AB1. Ответ: α = MNB1A.
Cлайд 9
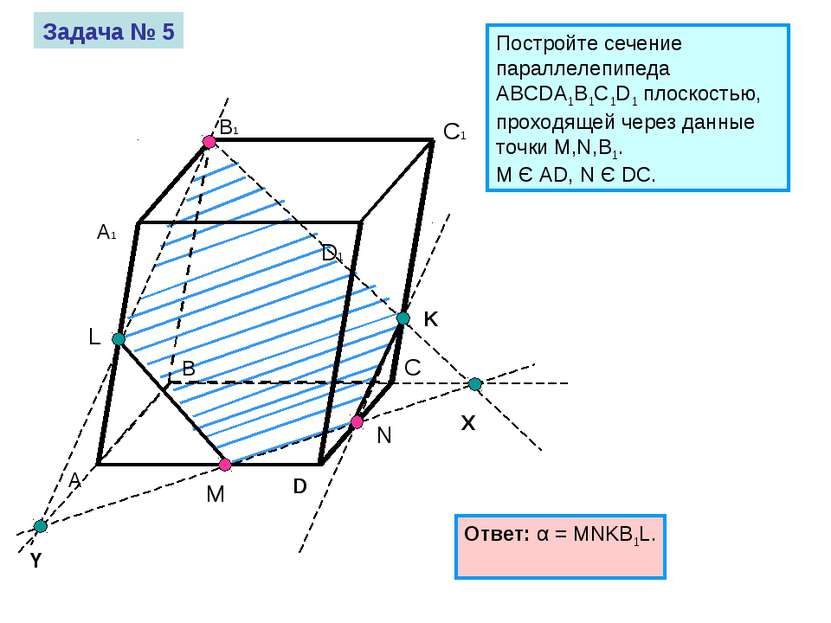
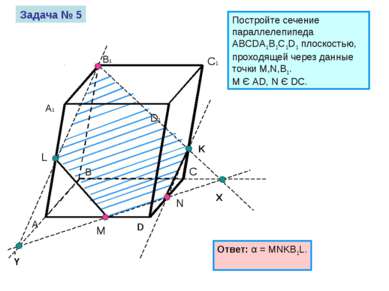Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через данные точки M,N,В1. M Є AD, N Є DC. B C D A1 B1 C1 D1 A M N Задача № 5 Ответ: α = MNKB1L.
Cлайд 10
Задачи для самостоятельного решения (работа в группах) План работы Решение задач №6 -№9 защита решений (чертеж на доске) обсуждение способов решения задачи проверка с помощью презентации Задача № 6 Задача № 7 Задача № 8 Задача № 9
Cлайд 11
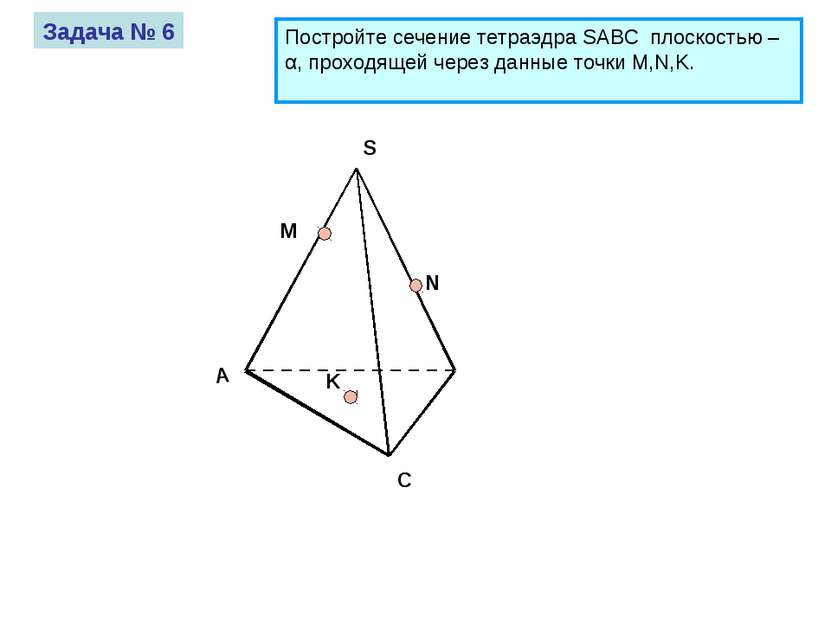
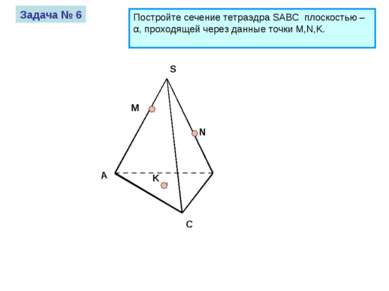А S C M N K Задача № 6 Постройте сечение тетраэдра SABC плоскостью – α, проходящей через данные точки M,N,K.
Cлайд 12
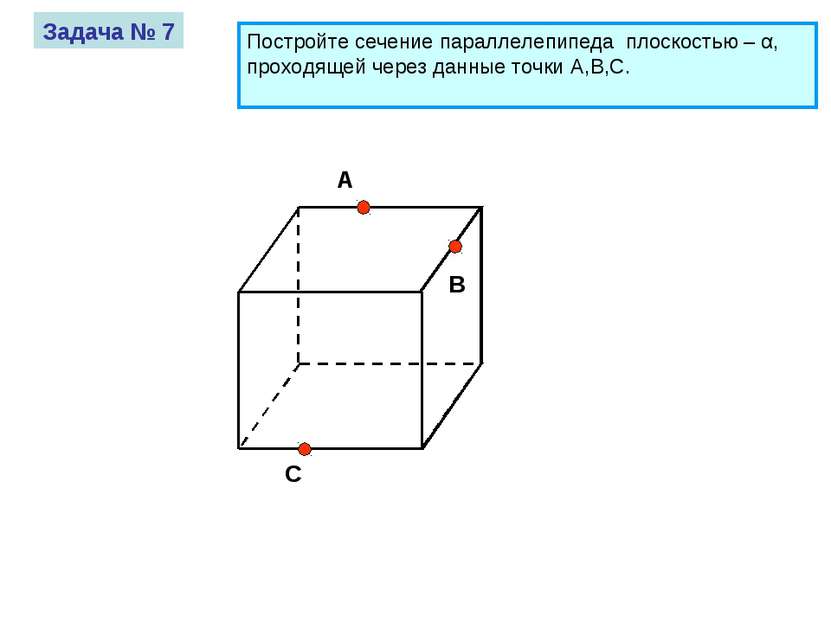
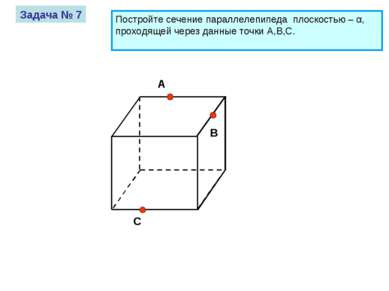A B C Задача № 7 Постройте сечение параллелепипеда плоскостью – α, проходящей через данные точки A,B,C.
Cлайд 13
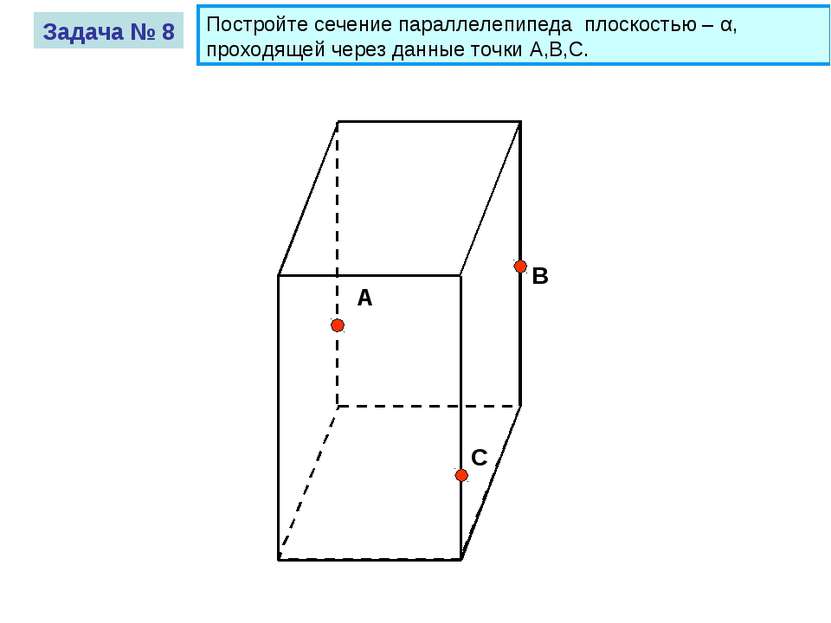
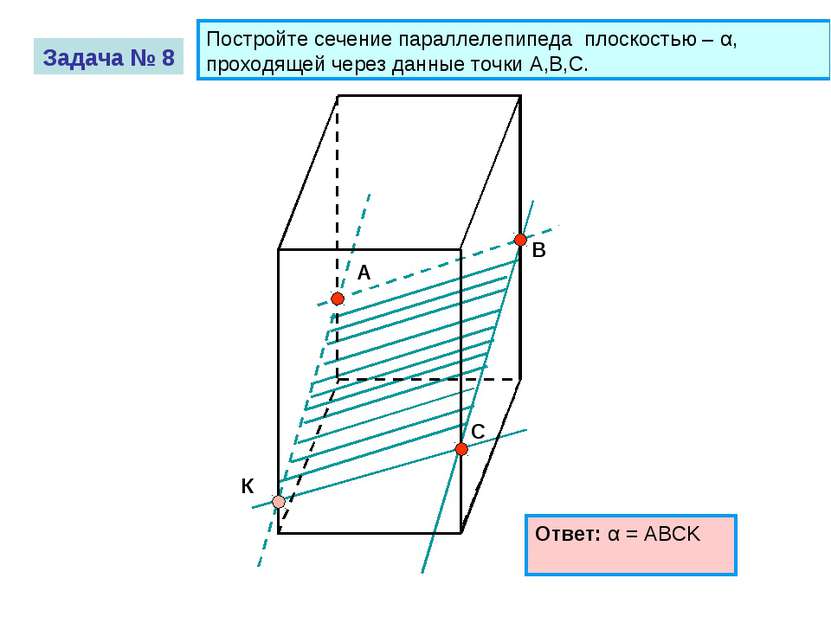
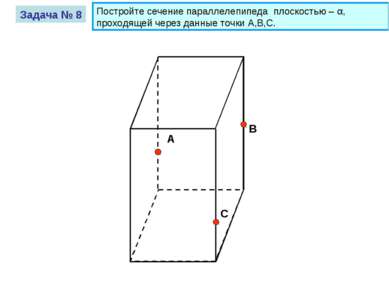Постройте сечение параллелепипеда плоскостью – α, проходящей через данные точки A,B,C. А В С Задача № 8
Cлайд 14
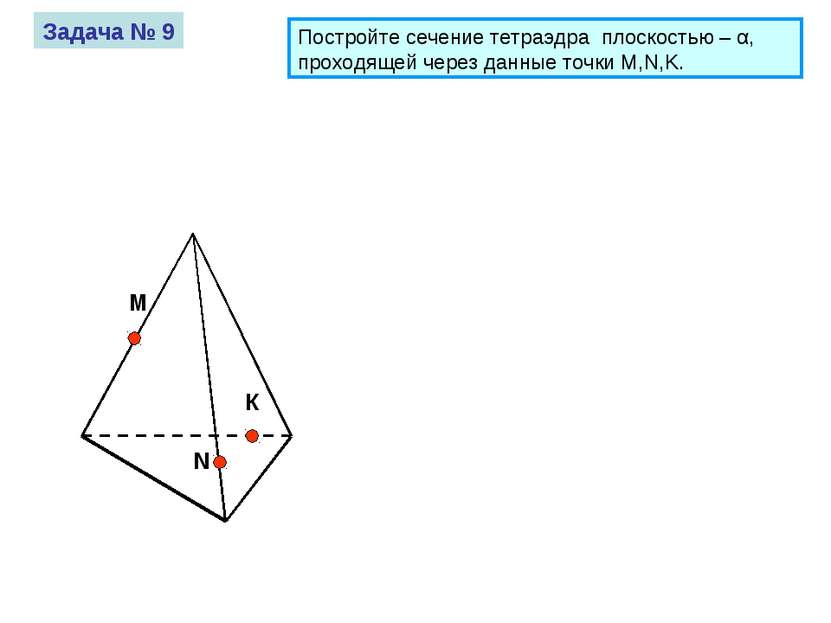
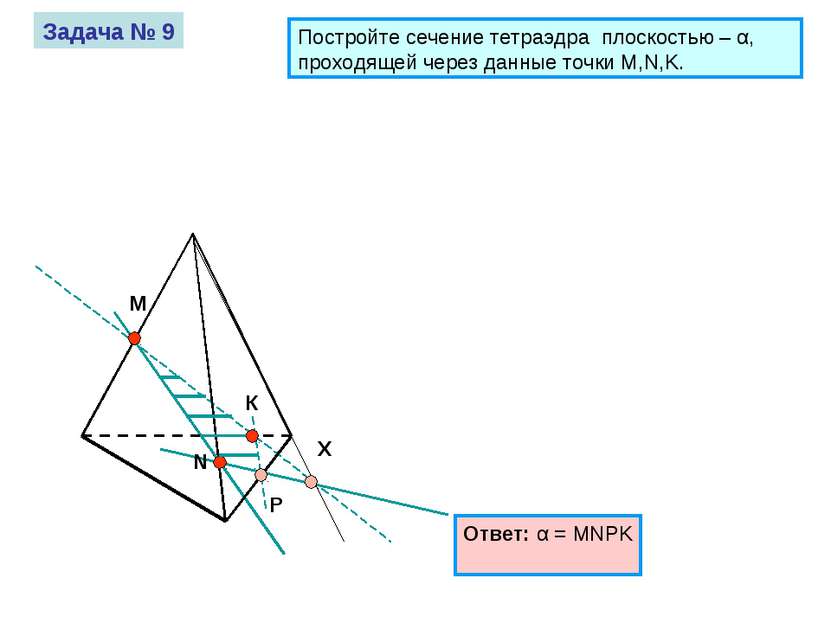
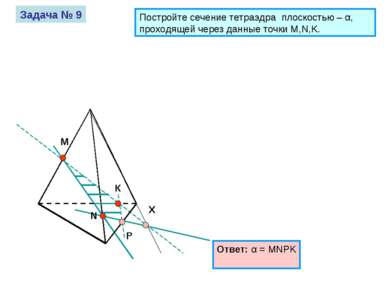
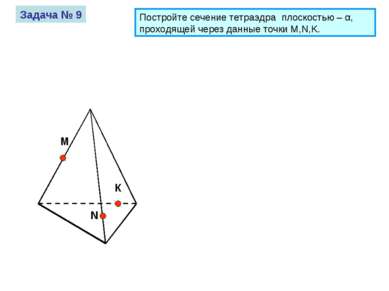М К N Задача № 9 Постройте сечение тетраэдра плоскостью – α, проходящей через данные точки M,N,K.
Cлайд 15
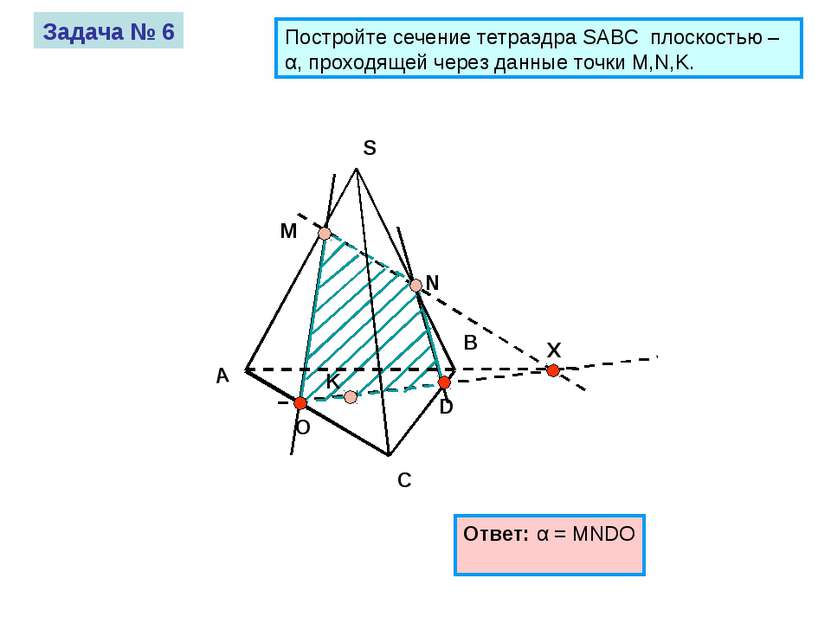
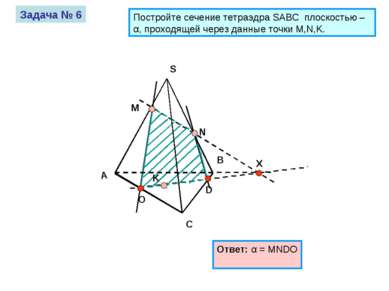А S B C M N K Задача № 6 Постройте сечение тетраэдра SABC плоскостью – α, проходящей через данные точки M,N,K. Ответ: α = MNDO
Cлайд 16
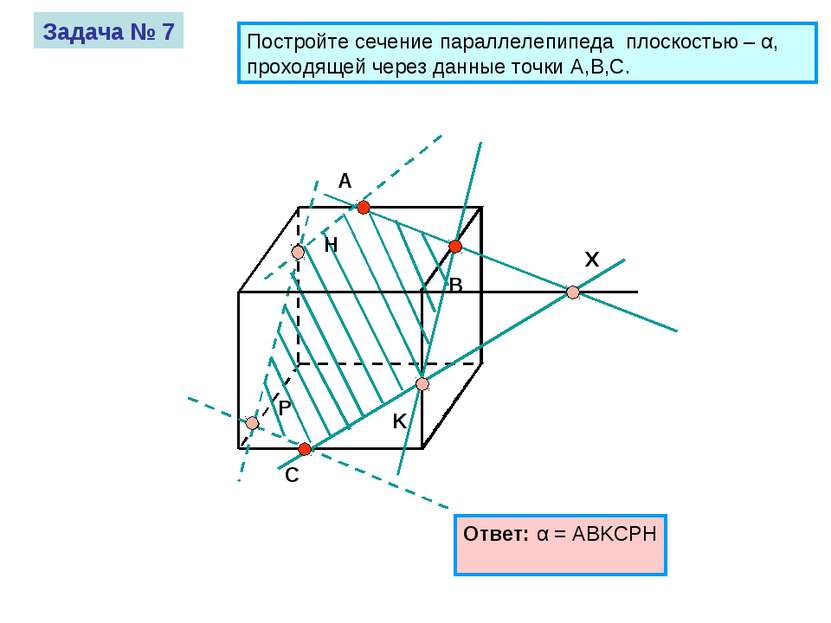
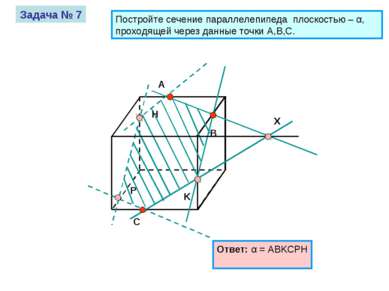A B C Задача № 7 Постройте сечение параллелепипеда плоскостью – α, проходящей через данные точки A,B,C. Ответ: α = ABKCPH
Cлайд 17
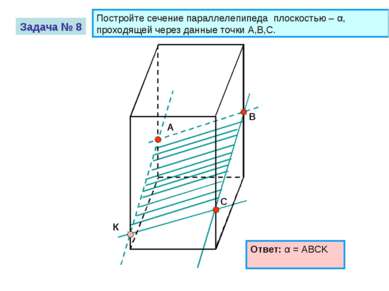А В С Задача № 8 Постройте сечение параллелепипеда плоскостью – α, проходящей через данные точки A,B,C. Ответ: α = ABCK
Cлайд 18
М К N Задача № 9 Постройте сечение тетраэдра плоскостью – α, проходящей через данные точки M,N,K. Ответ: α = MNPK
Cлайд 19
Верно ли построены сечения? А В С К М N L а) б)
Cлайд 20
Верно ли построены сечения? A B C P P A B C в) г)
