X
Код презентации скопируйте его
Наибольшее и наименьшее значение функции
Скачать эту презентацию
Презентация на тему Наибольшее и наименьшее значение функции
Скачать эту презентациюCлайд 1
Cлайд 2
Цель урока: Применение производной к нахождению наибольших и наименьших значений функций, к решению простейших прикладных задач «на экстремум»: Алгебраического смысла; Геометрического смысла.
Cлайд 3
«Идея функциональной зависимости в чистом виде выступает в тот момент, когда появляется алгебраическая формула или «алгебраическое выражение»». Дубнов Я.С.
Cлайд 4
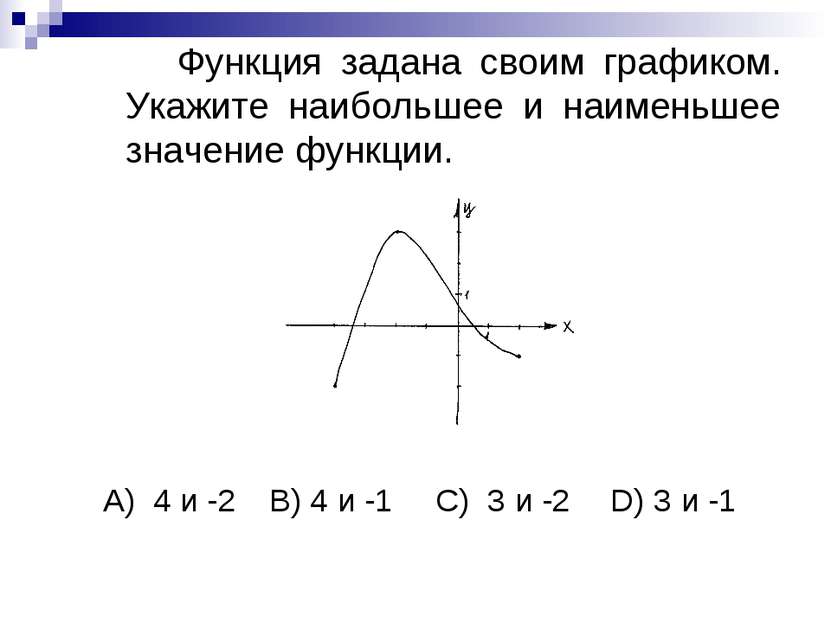
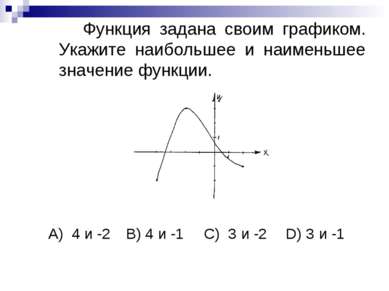Функция задана своим графиком. Укажите наибольшее и наименьшее значение функции. А) 4 и -2 B) 4 и -1 C) 3 и -2 D) 3 и -1
Cлайд 5
Найдите наибольшее значение функции f(x)=5-х2 А) -11 B) 8 C) 4 D) 5
Cлайд 6
3. Найдите наименьшее значение функции f(x)= 3 sin x на отрезке . А) 0 B) -3 C) -1 D) такого значения нет
Cлайд 7
4.Какая из функций имеет максимум? А) y =x3 B) y= C) y= D) y= 2x-x2
Cлайд 8
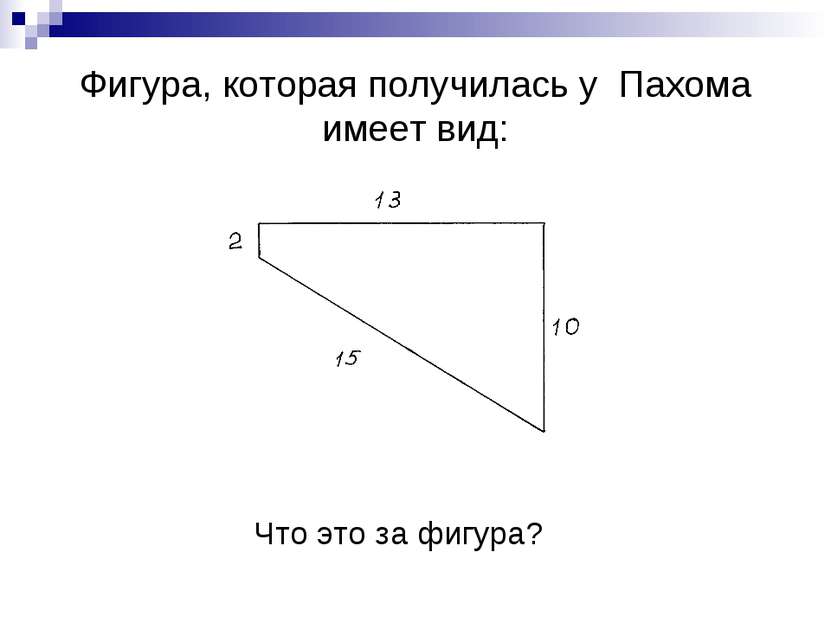
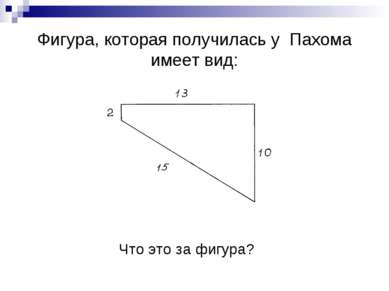
Рассказ «Много ли человеку земли нужно» О крестьянине Пахоме, покупавшем землю у башкирцев. -А цена какая будет?- говорит Пахом. -Цена у нас одна: 1000 рублей за день. Не понял Пахом. -Какая же это мера – день? Сколько в ней десятин будет? -Мы этого, - говорит, - не умеем считать. А мы за день продаем; сколько обойдешь в день, то и твое, а цена 1000 рублей. Удивился Пахом. -Да ведь это, - говорит, -в день обойти земли много будет. Засмеялся старшина. -Вся твоя, - говорит. – Только один уговор: если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги. -А как же, - говорит, - отметить , где я пройду? -А мы встанем на место, где ты облюбуешь; мы стоять будем, а ты иди, делай круг, а с собой скребку возьми и, где надобно, замечай, на углах ямки рой, дернички клади; потом с ямки на ямку плугом пройдем. Какой хочешь круг забирай, только до захода солнца приходи к тому месту, с какого взялся. Что обойдешь, все твое. Л.Н. Толстой
Cлайд 9
Фигура, которая получилась у Пахома имеет вид: Что это за фигура?
Cлайд 10
Задача: Периметр прямоугольника равен 60см. Какую длину должны иметь стороны прямоугольника, чтобы площадь была наибольшей?
Cлайд 11
Задача: На параболе y=x2 найдите точку, ближайшую к точке А(2; 0,5)
Cлайд 12
«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!» Пойа Д.
