X
Код презентации скопируйте его
Координаты вектора
Скачать эту презентацию
Презентация на тему Координаты вектора
Скачать эту презентациюCлайд 1
КООРДИНАТЫ ВЕКТОРА Отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим , , векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.
Cлайд 2
КООРДИНАТЫ ВЕКТОРА Теорема. Вектор имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде Доказательство. Отложим вектор от начала координат и его конец обозначим через А. Имеет место равенство Точка А имеет координаты (x, y, z) тогда и только тогда, когда выполняются равенства и, значит,
Cлайд 3
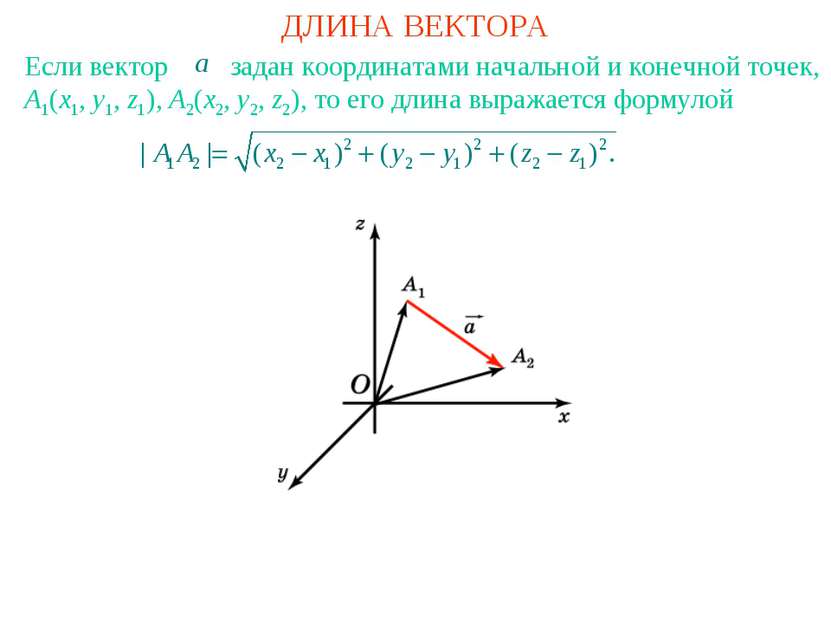
ДЛИНА ВЕКТОРА Если вектор задан координатами начальной и конечной точек, A1(x1, y1, z1), A2(x2, y2, z2), то его длина выражается формулой
Cлайд 4
Упражнение 1 Найдите координаты векторов: а) б) в) г) Ответ: а) (-2, 6, 1); б) (1, 3, 0); в) (0, -3, 2); г) (-5, 0, 5).
Cлайд 5
Упражнение 2 Найдите координаты вектора , если: a) A(2, -6, 9), B(-5, 3, -7); б) A(1, 3, -8), B(6, -5, -10); в) A(-3, 1, -20), B(5, 1, -1). Ответ: а) (-7, 9, -16); б) (5, -8, -2); в) (8, 0, 19).
Cлайд 6
Упражнение 3 Вектор имеет координаты (a,b,c). Найдите координаты вектора . Ответ: (-a, -b, -c).
Cлайд 7
Упражнение 4 В прямоугольном параллелепипеде OABCO1A1B1C1 вершина O – начало координат, ребра OA, OC, OO1 лежат на осях координат Ox, Oy и Oz соответственно и OA=2, OC=3, OO1=4. Найдите координаты векторов , , , . Ответ: (2, 0, 4); (2, 3, 4); (0, 0, 4); (0, 3, 0).
Cлайд 8
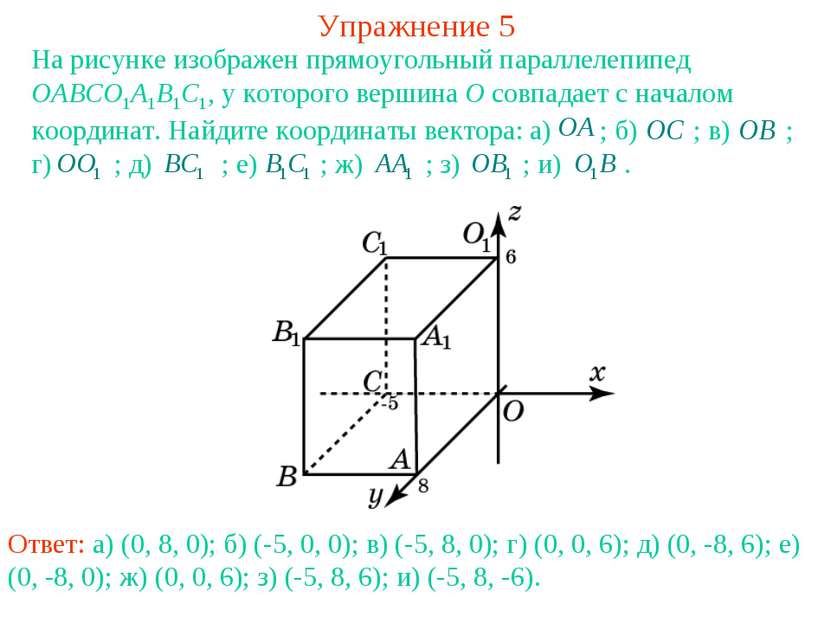
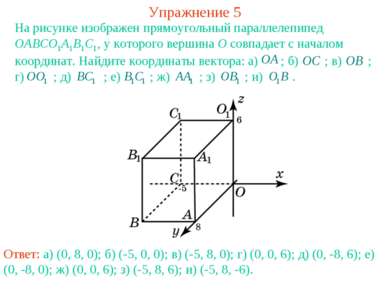Упражнение 5 На рисунке изображен прямоугольный параллелепипед OABCO1A1B1C1, у которого вершина O совпадает с началом координат. Найдите координаты вектора: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) . Ответ: а) (0, 8, 0); б) (-5, 0, 0); в) (-5, 8, 0); г) (0, 0, 6); д) (0, -8, 6); е) (0, -8, 0); ж) (0, 0, 6); з) (-5, 8, 6); и) (-5, 8, -6).
Cлайд 9
Упражнение 6 Найдите координаты векторов и , если (1, 0, 2), (0,3,-4). Ответ: (1, 3, -2); (1, -3, 6).
Cлайд 10
Упражнение 7 Даны векторы (-1,2,8) и (2,-4,3). Найдите координаты векторов: а) ; б) ; в) .
Cлайд 11
Упражнение 8 Найдите координаты точки N, если вектор имеет координаты (4, -3, 0) и точка M - (1, -3, -7). Ответ: (5, -6, -7).
Cлайд 12
Упражнение 9 Какому условию должны удовлетворять координаты вектора, чтобы он был: а) перпендикулярен координатной плоскости Oxy; б) параллелен координатной прямой Ox? Ответ: а) Первая и вторая координаты равны нулю; б) вторая и третья координаты равны нулю.
Cлайд 13
Упражнение 10 Найдите координаты конца единичного вектора с началом в точке A(1, 2, 3) и: а) перпендикулярного плоскости Oxy; б) параллельного прямой Ox. Ответ: а) (1,2,4), (1,2,2); б) (2,2,3), (0,2,3).
Cлайд 14
Упражнение 11 Найдите длину вектора: а) б) в)
