X
Код презентации скопируйте его
Двумерный симплекс история его изучения
Скачать эту презентацию
Презентация на тему Двумерный симплекс история его изучения
Скачать эту презентациюCлайд 1
Выполнила: ученица 8 Б класса МОУ СОШ № 29 г. Ставрополя НИКИТИНА АЛЕНА
Cлайд 2
На уроках геометрии в 7 классе мы изучали треугольник и его свойства. Небольшие исторические справки к изучаемому материалу показали, что знание об этой фигуре развивалось постепенно. Не мало ученых изучали треугольник, формулировали новые задачи, открывали свойства и создалось впечатление, что изучение треугольника еще не завершено и возможны еще новые открытия. Многие факты остались за страницами школьного учебника и мы попытались приоткрыть некоторые тайны. АКТУАЛИЗАЦИЯ ПРОБЛЕМЫ РАБОЧАЯ ГИПОТЕЗА
Cлайд 3
ЦЕЛЬ МОЕГО ПРОЕКТА Изучить материалы и существующую литературу по данному вопросу. Понять роль этой геометрической фигуры в человеческой деятельности. Создать исторический фон, соотнести материал изучаемый в школьном курсе с историей развития человечества.
Cлайд 4
Работая над проектом, я искала информацию в справочниках, энциклопедиях и в Интернете. Некоторые факты показавшиеся мне удивительными отражены в моей презентации
Cлайд 5
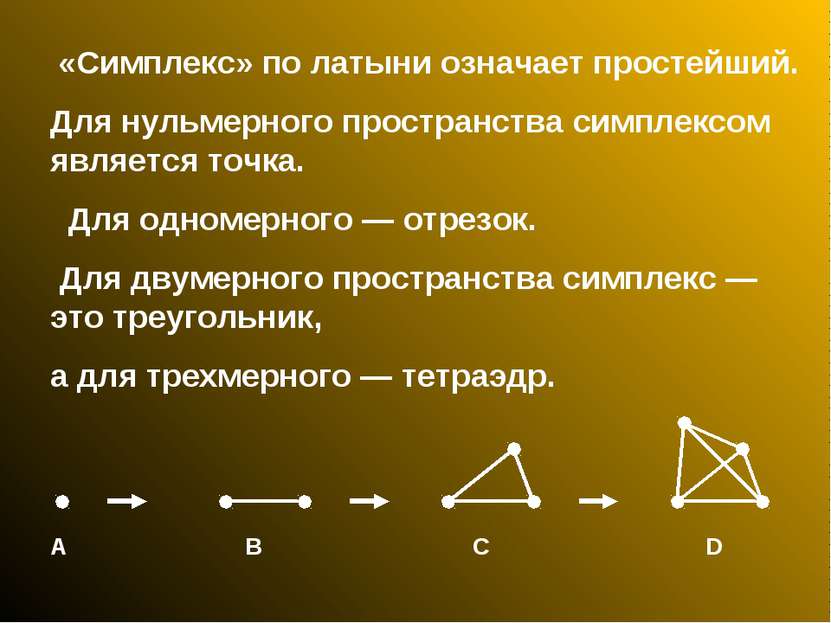
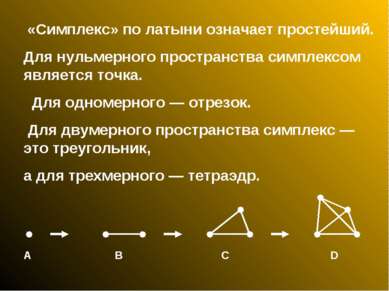«Симплекс» по латыни означает простейший. Для нульмерного пространства симплексом является точка. Для одномерного — отрезок. Для двумерного пространства симплекс — это треугольник, а для трехмерного — тетраэдр. A B C D
Cлайд 6
Треугольник – это простейшая фигура: три стороны и три вершины
Cлайд 7
Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников.
Cлайд 8
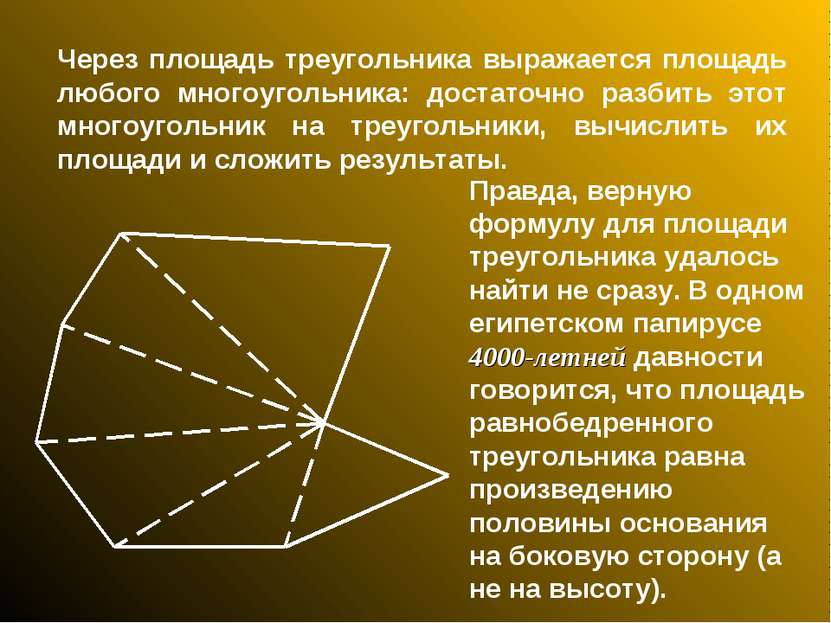
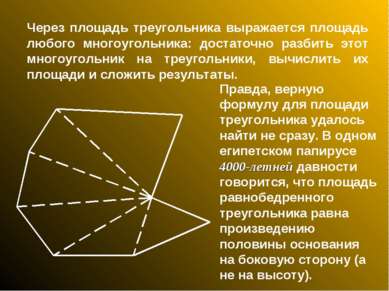Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).
Cлайд 9
Через 2000 лет в Древней Греции изучение свойств треугольника ведется очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны. Становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.
Cлайд 10
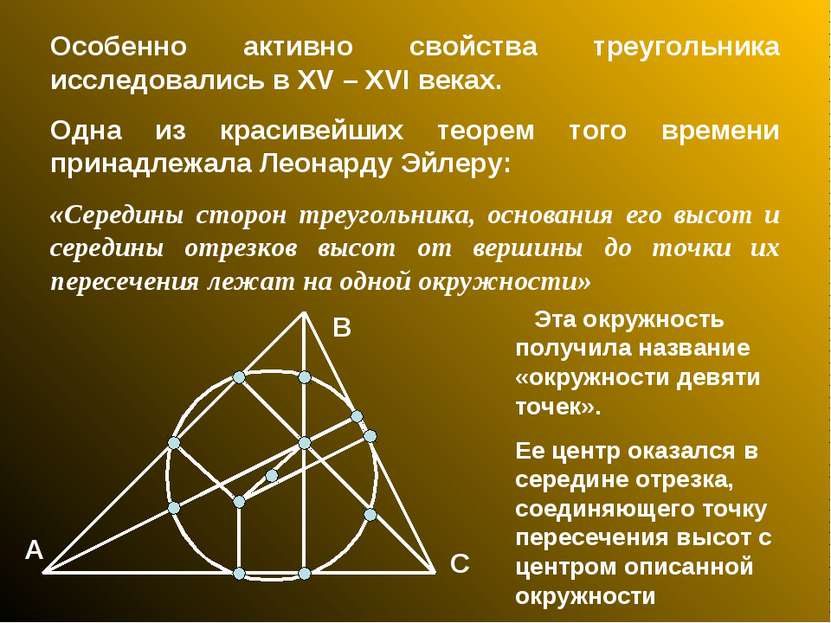
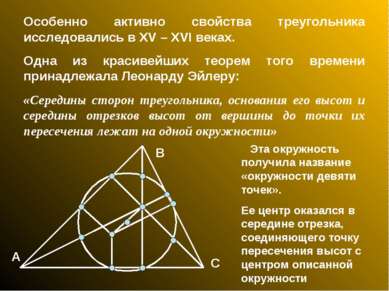Особенно активно свойства треугольника исследовались в XV – XVI веках. Одна из красивейших теорем того времени принадлежала Леонарду Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности» А В С Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности
Cлайд 11
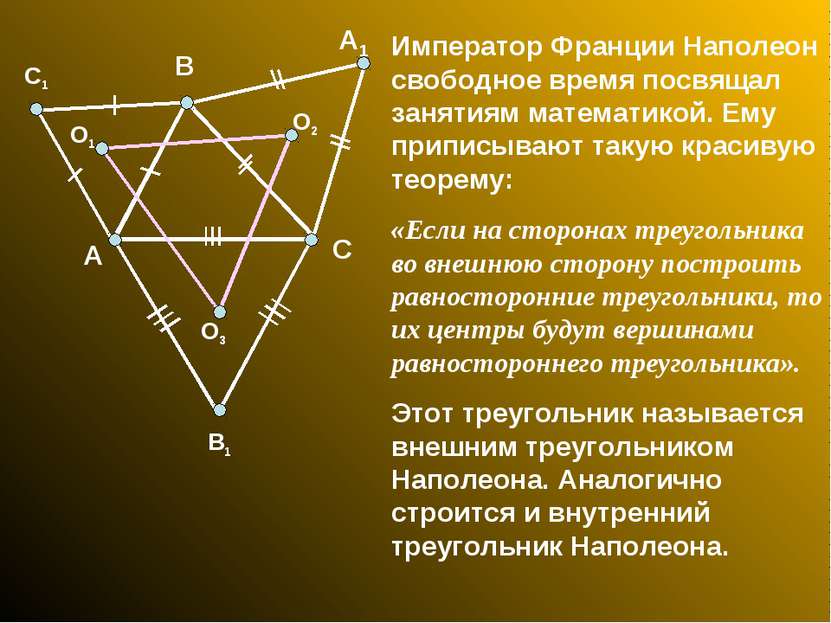
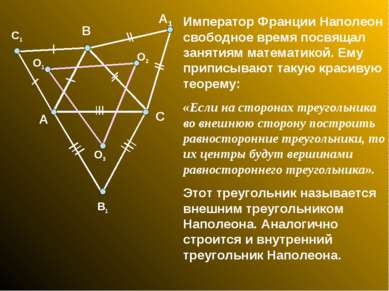Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывают такую красивую теорему: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник называется внешним треугольником Наполеона. Аналогично строится и внутренний треугольник Наполеона. А В С О1 О2 О3 В1 С1 А1
Cлайд 12
Огромное количество работ по геометрии треугольника, проведенное в XV – XIX веках, создало впечатление, что о треугольнике уже известно все. Тем удивительнее было открытие, сделанное американским математиком Ф. Морли. «Если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника».
Cлайд 13
ЭТАПЫ РАЗВИТИЯ МАТЕМАТИКИ I. ЗАРОЖДЕНИЕ МАТЕМАТИКИ (Первобытнообщинный строй, каменный век, рабовладельческий строй): Оформление чувства геометрическ- ой фигуры, папирус Ахмеса (ок 2000 до н.э.), II. ПЕРИОД ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ (Разложение первобытного строя, зарождение классов, VI в до н.э.- XVI вв) Свойства плоских фигур, задачи на вычисления площадей и объемов, зарождение сферической геометрии… III. СОЗДАНИЕ МАТЕМАТИКИ ПЕРЕМЕННЫХ ВЕЛИЧИН (Зарождение капитализма, образование США, Петровская эпоха в России , раннее новое время) Аналитическая геометрия, … IV.СОВРЕМЕННАЯ МАТЕМАТИКА (Развитие капитализма, Наполеоновская эпоха, империализм … XX-XXI вв) Вопросы обоснования математики, математические модели, неевклидова геометрия…
Cлайд 14
ВЫВОДЫ: В результате проведенных исследований материалов по рассматриваемому вопросу я узнала, что Треугольник изучался на протяжении всего развития цивилизованного общества. «Задачи для оттачивания ума» были интересны не только ученым математикам, но и любителям и, даже, некоторым известным «нематематикам». Треугольник и его свойства проявляются во всех областях жизни человека: архитектуре, землемерии, астрономии, строительстве, химии, психологии, рекламе и т.д
Cлайд 15
Литература, которой я пользовалась: Энциклопедия для детей. Т.11. Математика. Главный редактор М.Д. Аксенова.- М:Аванта+,1999.-688с.: ил. Математика: Школьная энциклопедия. Гл. ред. С. М. Никольский. – М.: Большая Российская энциклопедия; Дрофа, 1997. – 527 с.: ил. Большая Советская Энциклопедия. Главный редактор Б.А. Введенский, том 4, второе издание, государственное научное издательство «Большая советская энциклопедия», 667с.
