X
Код презентации скопируйте его
Геометрические задачи на экстремум
Скачать эту презентацию
Презентация на тему Геометрические задачи на экстремум
Скачать эту презентациюCлайд 1
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ЭКСТРЕМУМ Задачи на нахождение наибольшего или наименьшего значения Мама - null
Cлайд 2
Определения Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть задачами «на экстремум» или задачами «на максимум и минимум». Extremum (лат.)-крайний Maximum (лат.)-наибольший Minimum (лат.)-наименьший Задачи, в которых фигура с экстремальными свойствами отыскивается среди других с равными периметрами. Называются изопериметрическими или «задачами Дидоны».
Cлайд 3
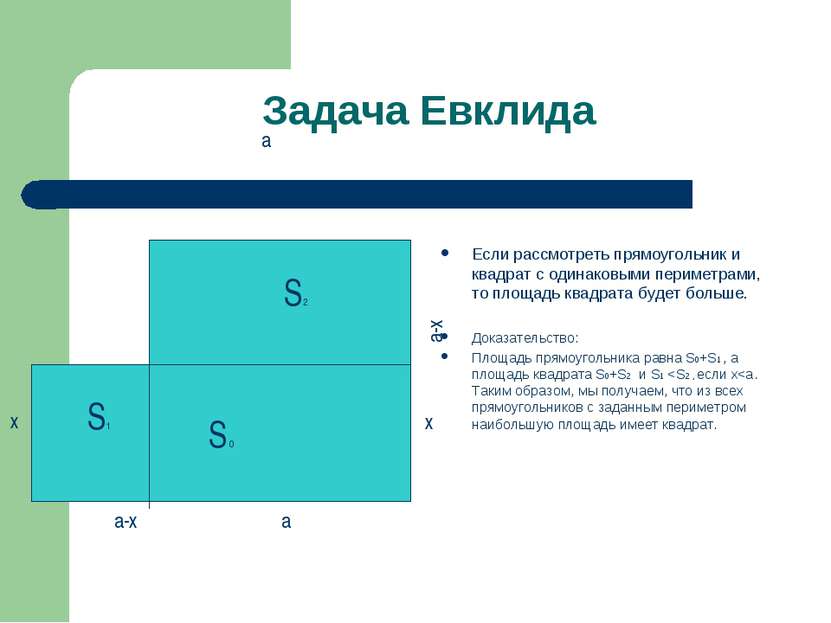
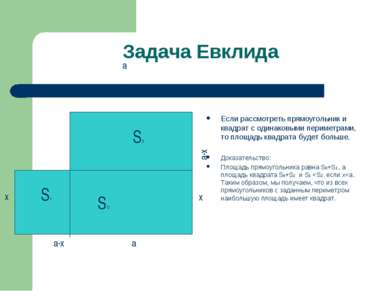Задача Евклида Если рассмотреть прямоугольник и квадрат с одинаковыми периметрами, то площадь квадрата будет больше. Доказательство: Площадь прямоугольника равна S0+S1 , а площадь квадрата S0+S2 и S1
Cлайд 4
Легенда о Дионе Диона- основательница города Карфагена и его первая царица. Вынужденная бежать из своего города, Диона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Диона разрезала воловью шкуру на узкие ремешки и, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было покрыть воловьей одной шкурой .
Cлайд 5
Задачи Зенодора (2-1 в. до н.э.) Из всех многоугольников с равным периметром и равным числом сторон наибольшую площадь имеет правильный многоугольник Из двух правильных многоугольников с равным периметром большую площадь имеет тот, у которого число углов больше Из всех плоских фигур с равным периметром наибольшую площадь имеет круг.
Cлайд 6
Задача Дионы (частный случай) Если принять, что береговая линия есть прямая и ограничиваемый участок прямоугольной формы, то наибольшую площадь будет иметь прямоугольник с длинами сторон р/4 и р/2. Р-ПЕРИМЕТР УЧАСТКА. море берег участок р/4 Р/2
Cлайд 7
ПРИМЕНЕНИЕ НЕРАВЕНСТВ Задача. Каких размеров должен быть ящик, чтобы при заданной площади поверхности его объем был наибольшим? Решение. Пусть а, b и с- длины ребер. S-площадь полной поверхности, V- объем. S=2(ab+bc+ac), V=abc. Применим неравенство: среднее арифметическое больше или равно среднему геометрическому Знак равенства достигается при a=b=c и при этом объем будет наибольшим. Итак, наибольший объем имеет куб.
