X
Код презентации скопируйте его
Конус. Понятие конуса. Площадь поверхности конуса. Усеченный конус
Скачать эту презентациюПрезентация на тему Конус. Понятие конуса. Площадь поверхности конуса. Усеченный конус
Скачать эту презентациюCлайд 4
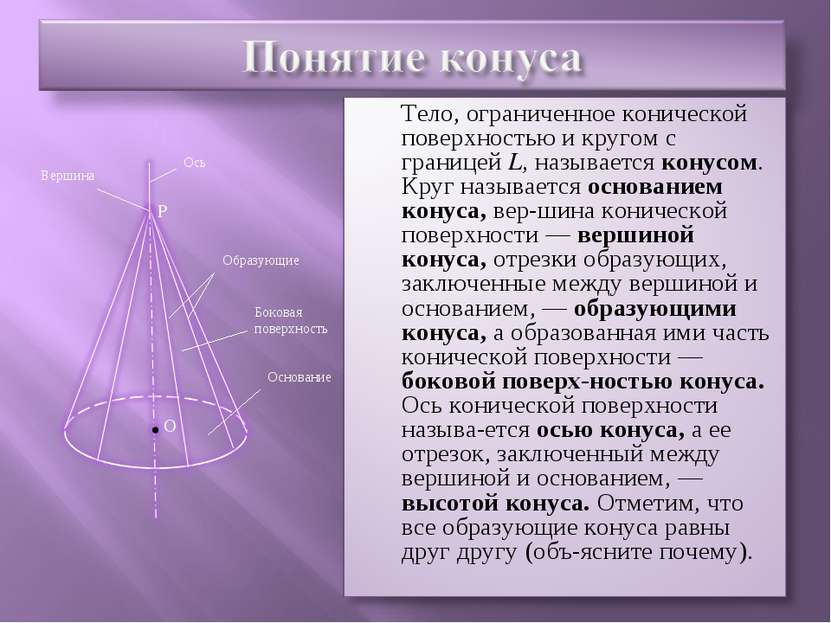
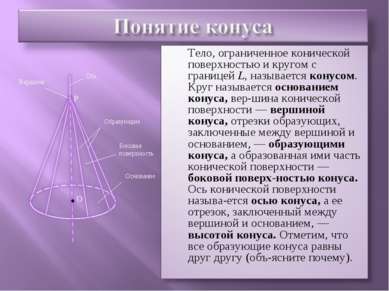
 Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке изображен конус, полученный вращением прямоугольного треугольника ABC вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС. А С
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке изображен конус, полученный вращением прямоугольного треугольника ABC вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС. А С
Cлайд 6
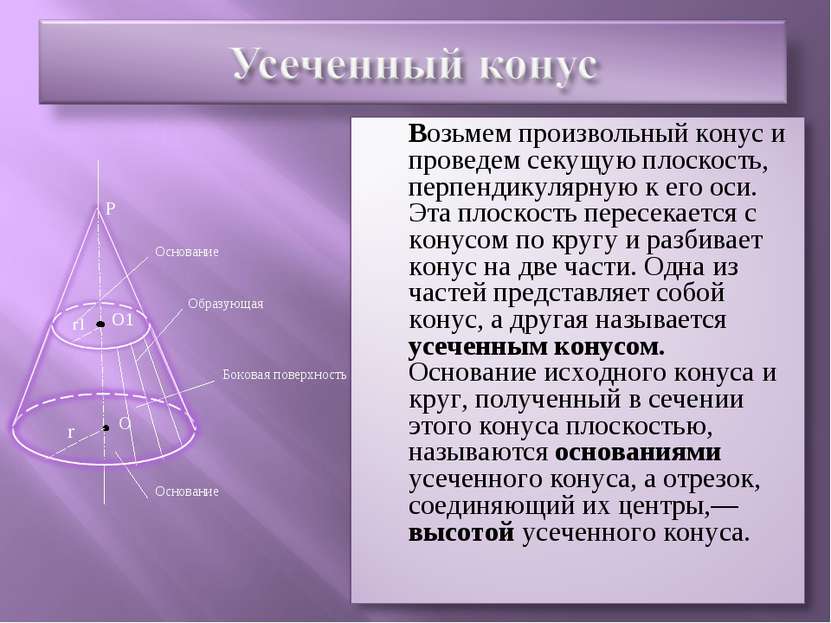
 Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О и расположенным на оси, конуса. Радиус r1 этого круга равен (ОР/РО1)*r, где r - радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1. P M О1 r r1 M1 α
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О и расположенным на оси, конуса. Радиус r1 этого круга равен (ОР/РО1)*r, где r - радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1. P M О1 r r1 M1 α
Cлайд 8
 За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь Sбoк боковой поверхности конуса через его образу ющую I и радиус основания r. Площадь кругового сектора — развертки боковой поверхности конуса равна πl2α 360 Где α – градусная мера дуги АВАI , поэтому
За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь Sбoк боковой поверхности конуса через его образу ющую I и радиус основания r. Площадь кругового сектора — развертки боковой поверхности конуса равна πl2α 360 Где α – градусная мера дуги АВАI , поэтому