X
Код презентации скопируйте его
Задачи по ядерной физике
Скачать эту презентацию
Презентация на тему Задачи по ядерной физике
Скачать эту презентациюCлайд 1
Задачи по ядерной физике Отличительные особенности: Прикладная направленность 2. Выход за рамки школьного учебника Презентации по ядерной физике http://prezentacija.biz/prezentacii-po-fizike/
Cлайд 2
1. В кровь человека ввели небольшое количество раствора, содержащего Na24 с активностью А0 = 2000 Бк. Активность 1 см крови через 5 ч оказалась равной А’ = 0,267 Бк. Период полураспада данного радиоизотопа Т = 15 ч. Найти объем крови человека. Чтобы решить задачу необходимо: Получить формулу активности A = |dN/dt|, для этого целесообразно использовать уравнение распада в виде N = N0 exp(- t), где постоянная распада выражается через период полураспада ½ N0 = N0 exp(- T) =ln2/T A = |- N0 exp(- t)| =|- N|=(ln2/T)N
Cлайд 3
2. Необходимо сказать, что активность по данной формуле находится во всем объеме крови. 3. Необходимо обратить внимание учащихся на равенство концентраций радиоактивного вещества во всем объеме крови и в пробе (если не поймут – напомнить задачу с озером и кусочком соли ) n = N/V = N’/V’ V = V’N/N’ 4. Напомнить, что отношение числа не распавшихся частиц равно отношению активностей, поэтому, V = V’A/A’ = V’A0 (2-t/T )/A Теперь, получив пропорциональность активности числу распадов, можно записать уравнение распада в знакомом виде и, обозначив A0 = (ln2/T)N0 Можно записать формулу активности в любой момент времени A = A0 2-t/T
Cлайд 4
2. Удельная активность препарата, состоящего из активного Со58 и неактивного Со59, составляет 2,2 10 Бк/г Период полураспада Со58 равен 71,3 суток. Найти отношение массы активного Со58 в этом препарате к массе препарата. Для решения необходимо: Определить понятие удельной активности – обратить внимание на размерность Бк/г = [A/m] Так как препарат состоит из активного и неактивного компонент, получим m = m(58) +m(59) 3. Активность находим только для Со58 , поэтому A = A(58)= A0 = N0 = (ln2/T)N0
Cлайд 5
4. Удельная активность препарата составит A/m= (ln2/T)N0 /m 5. Число частиц активного элемента в граммах, так как удельная активность отнесена к граммам, N0 = (m(58)/58) NА 6. Подставляем число частиц в активность и получаем A/m= (ln2/58 T) [m(58)/m] NA m(58)/m = NA A/m (58T/ln2)
Cлайд 6
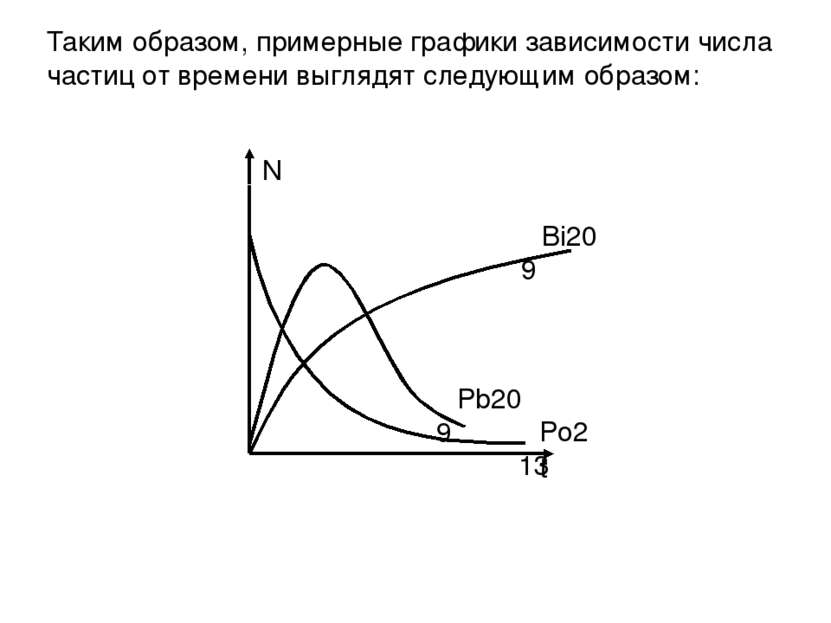
3. Радиоактивные ядра А испытывают превращения по цепочке А1 А2 А3 (например Po213 Pb209 Bi 209 ) c соответствующими периодами полураспада Т1 , Т2 , Т3 . В начальный момент препарат содержал только изотопы ядра А1 в количестве N01 . Возможные вопросы задачи: Опишите процесс превращения, постройте примерные графики зависимости от времени каждого изотопа Найдите закон накопления стабильных ядер A3 . Возможная задача по ядерной физике в поле С1
Cлайд 7
Для решения задачи чистого описания процесса необходимо: Определить характер распада: Po213 Pb209 + He24 - распад Pb209 Bi209 + e0-1 - распад 2. Число частиц изотопа Po изменяется по закону радиоактивного распада и имеет вид N1 = N01 2-t/T1 3. Число частиц изотопа Pb в начальный момент времени было равно нулю, потом оно растет , так как периоды полураспада Po и Pb разные, потом начинает убывать изменяясь по закону N2 = N02(t) 2-t/T2 =N01 (1 – 2-t/T1) 2-t/T2 4. Число частиц изотопа Bi изменяется по закону радиоактивного распада и имеет вид N3 = (N02 – N2 )2-t/T3
Cлайд 8
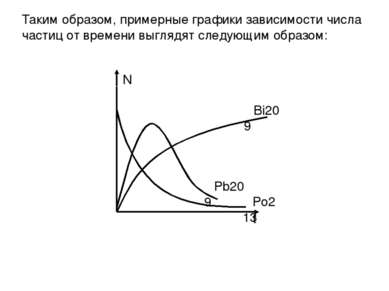Таким образом, примерные графики зависимости числа частиц от времени выглядят следующим образом:
Cлайд 9
4. Общее число частиц радиоактивного препарата, содержащего Po210 и Co58 , испытывающих - распад с периодами полураспада Т(Po) = 138 суток и Т(Co) = 71,3 суток приведено в таблице. По этим данным найти начальное число атомов Po210 и Co58 Чтобы решить задачу, необходимо: Обратить внимание, что в каждом столбце приведена сумма N = N1 + N2 числа частиц первого и второго изотопов, каждое из которых меняется по закону N1 = N01 2-t/T1 N1 = N01 2-t/T1 t,сут 0 50 100 150 200 250 N 1020 10 6,9 4,8 3,5 2,5 1,84
Cлайд 10
2. Записать закон распада для системы, выбрав два столбца таблицы (будем измерять число частиц в 1020) 10 = N10 + N20 6,9 = N10 2-t/T1 + N20 2-t/T2 3. Выполнить предварительный расчет, подставив значения времени t = 50 и T1 = 138 и Т = 71,3, получить систему линейных уравнений: 10 = N10 + N20 6,9 = 0,78N10 + 0,62N20 4. Решить систему и получить ответ N10 = 5,6 1020 N20 =4,4 1020
