X
Код презентации скопируйте его
Интерференция волн
Скачать эту презентацию
Презентация на тему Интерференция волн
Скачать эту презентациюCлайд 1
Тема урока: Интерференция волн
Cлайд 2
Принцип суперпозиции Точка, в которой «встретились» две волны, участвует в двух колебаниях. Результирующее смещение точки от положения равновесия равно сумме смещений, вызываемых каждой волной в отдельности
Cлайд 3
Что получится в результате сложения волн?
Cлайд 4
Что получится в результате сложения волн? Результат сложения зависит от разности фаз складывающихся колебаний (т.е. от того, в какой фазе приходит каждая волна в точку сложения)
Cлайд 5
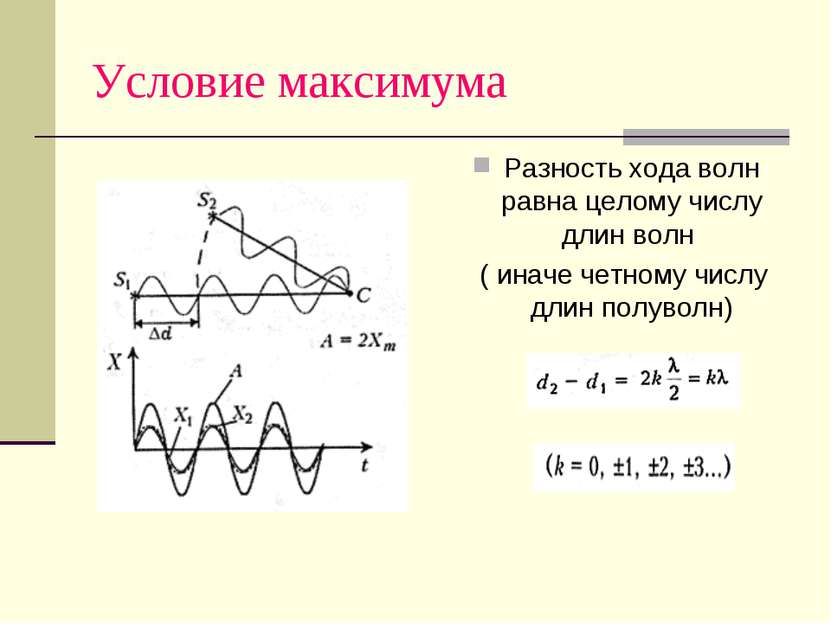
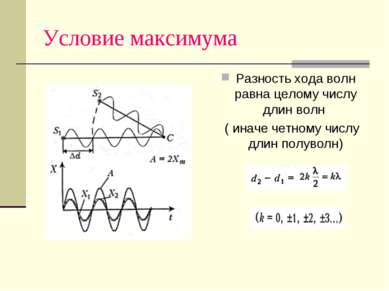Условие максимума Разность хода волн равна целому числу длин волн ( иначе четному числу длин полуволн)
Cлайд 6
Что получится в результате сложения волн? При этом амплитуда результирующего колебания максимальна – волны «усилили» друг друга
Cлайд 7
Условие минимума Разность хода волн равна нечетному числу длин полуволн.
Cлайд 8
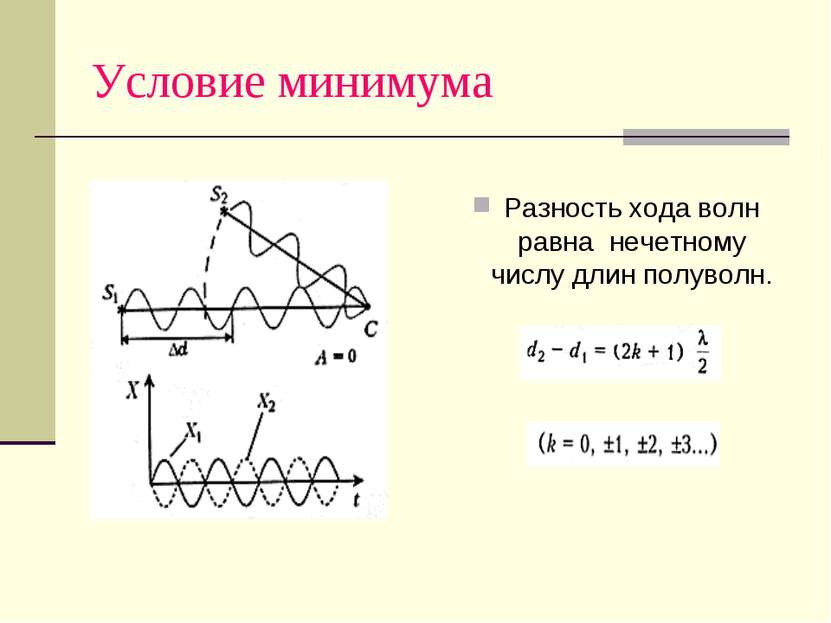
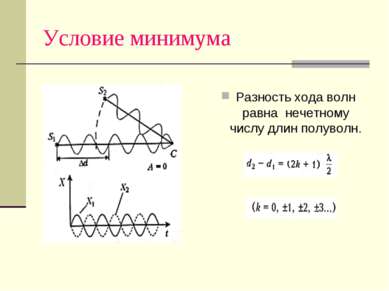
Что получится в результате сложения волн? Условие минимума: Разность хода равна нечетному числу длин полуволн ∆ d = ( 2k + 1 ) λ/2 При этом амплитуда результирующего колебания равна 0. Волны «погасили» друг друга
Cлайд 9
Как называется это явление? Интерференцией называется сложение волн, при котором происходит перераспределение амплитуд и энергий в результирующем колебании.
Cлайд 10
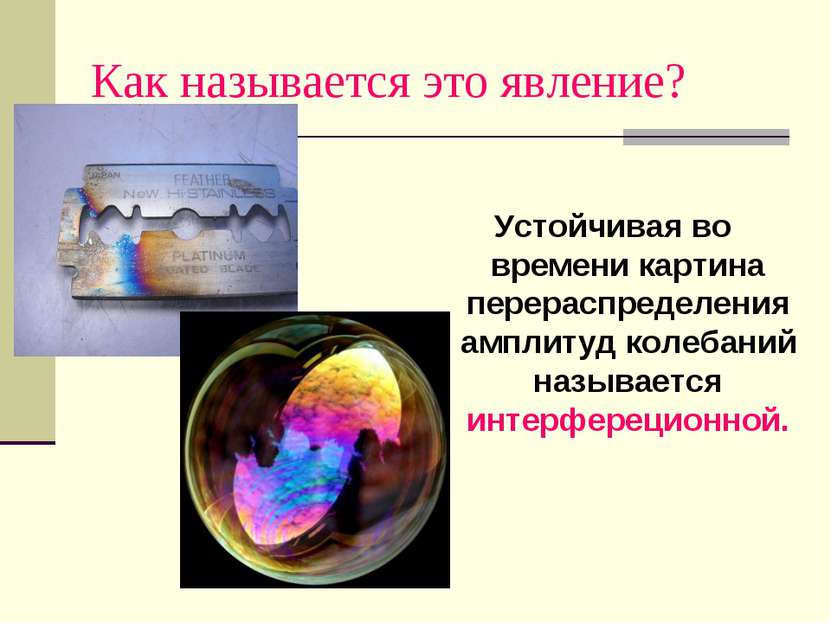
Как называется это явление? Устойчивая во времени картина перераспределения амплитуд колебаний называется интерфереционной.
Cлайд 11
Условия получения четкой интерференционной картины: Волны должны иметь одинаковую частоту и постоянную разность фаз. Такие волны называются когерентными.
Cлайд 12
Опыт Томаса Юнга
Cлайд 13
Опыт Юнга по наблюдению интерференции света
Cлайд 14
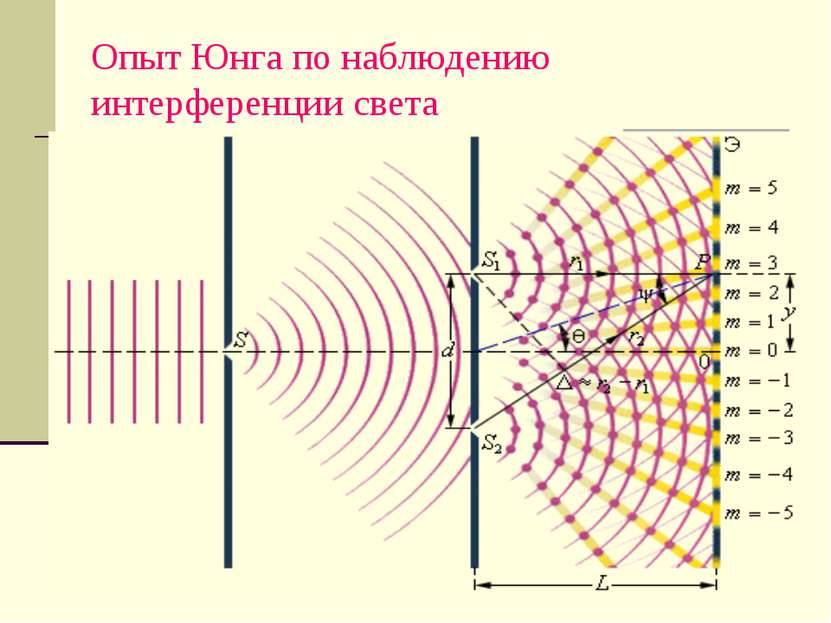
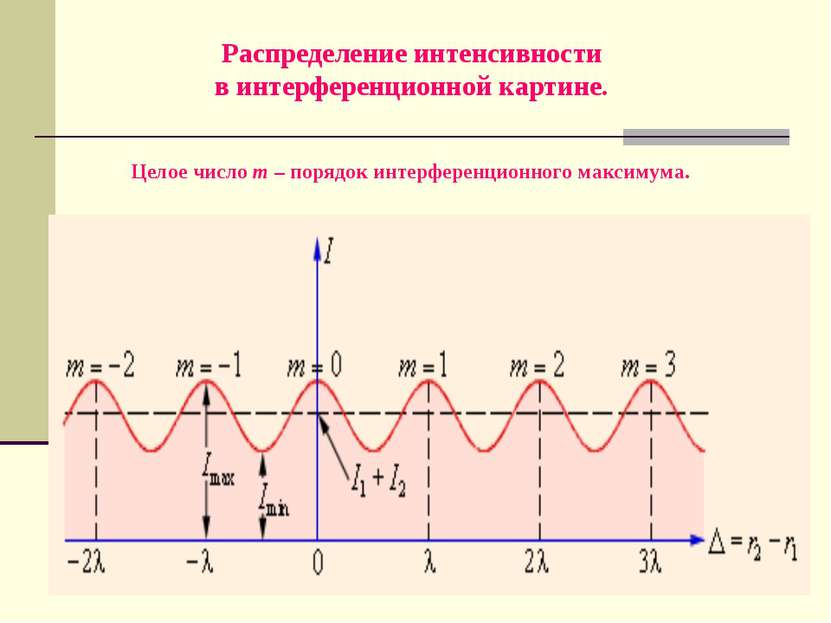
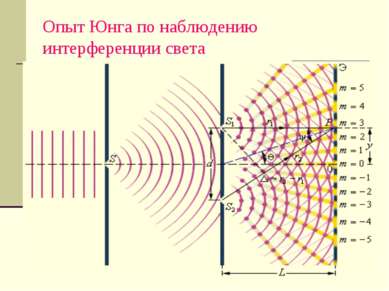
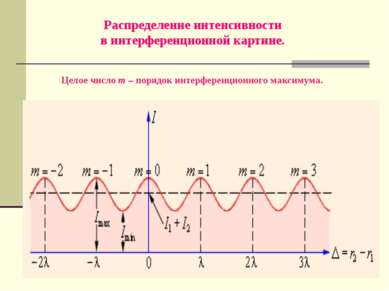Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума.
Cлайд 15
Наблюдение колец Ньютона Интерференция возникает при сложении волн, отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн; h – толщина воздушного зазора.
Cлайд 16
Наблюдение колец Ньютона Кольца Ньютона в монохромати-ческом свете (зеленом и красном)
Cлайд 17
Наблюдение колец Ньютона
Cлайд 18
Интерференция в тонких пленках
Cлайд 19
Интерференция в тонких пленках
Cлайд 20
Интерференция на мыльном пузыре
Cлайд 21
Интерференция света вокруг нас
