X
Код презентации скопируйте его
Взаимодействие гамма-квантов с веществом
Скачать эту презентацию
Презентация на тему Взаимодействие гамма-квантов с веществом
Скачать эту презентациюCлайд 1
Лекция 8 Процессы взаимодействия гамма-квантов Фотоэффект Характеристики сечения фотоэффекта Сечение фотоэффекта Направление вылета электрона Комптон-эффект Сечение комптон-эффекта на электроне Сечение комптон-эффекта на протоне «Взаимодействие гамма-квантов с веществом»
Cлайд 2
Э/м взаимодействие гамма-квантов: -фотоэффект; - упругое рассеяние на электронах (комптон-эффект); - рождение пар частиц. Процессы происходят в области энергий кэВ - сотни МэВ, которые наиболее часто используются в прикладных исследованиях. Рассмотрим зависимость от энергии Еγ и характеристик вещества Процессы взаимодействия гамма-квантов Связь между энергией γ-кванта и его длиной волны:
Cлайд 3
Фотоэффект Фотоэффект – это процесс выбивания электрона из нейтрального атома, под действием гамма-кванта Свободный электрон не поглощает гамма-квант Пусть реакция идет используем 4-импульсы Возведем в квадрат Преобразуем Последнее равенство оказывается справедливым, если Еγ = 0, т.е. гамма-кванта нет. Значит При фотоэффекте электрон получает энергию Ii – потенциал ионизации ТА- кинетическая энергия иона
Cлайд 4
Характеристики сечения фотоэффекта Фотоэффект возможен, если энергия γ-кванта больше потенциала ионизации (K, L, M…-оболочки) Если Еγ < Ik , то выбивание электронов происходит только с внешних оболочек L, M.. Выбивание электронов с внутренних оболочек сопровождается монохроматическим рентгеновским характеристическим излучением, возникающим при переходе атомного электрона на освободившийся уровень. При этом может возникать целый каскад взаимосвязанных переходов. Передача энергии иона одному или нескольким орбитальным электронам, приводит в вылету из атома электронов Оже.
Cлайд 5
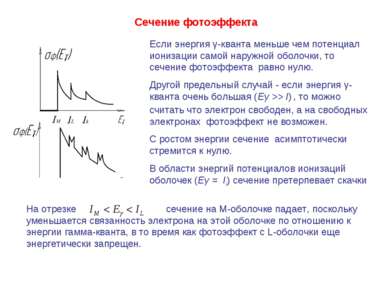Сечение фотоэффекта Если энергия γ-кванта меньше чем потенциал ионизации самой наружной оболочки, то сечение фотоэффекта равно нулю. Другой предельный случай - если энергия γ-кванта очень большая (Еγ >> I) , то можно считать что электрон свободен, а на свободных электронах фотоэффект не возможен. С ростом энергии сечение асимптотически стремится к нулю. В области энергий потенциалов ионизаций оболочек (Еγ = Ii) сечение претерпевает скачки На отрезке сечение на М-оболочке падает, поскольку уменьшается связанность электрона на этой оболочке по отношению к энергии гамма-кванта, в то время как фотоэффект с L-оболочки еще энергетически запрещен.
Cлайд 6
Влияние сильной связанности электрона в атоме на сечение фотоэффекта отражается в степенной зависимости от заряда ядра Квантово-механический расчет требует знания -функций атомных электронов на разных оболочках Эффективное сечение фотоэффекта с внутренней К-оболочки определяется соотношениями (см2/атом): если Еγ > mc2 Где томсоновское сечение рассеяния Сечение быстро падает Сечение фотоэффекта
Cлайд 7
Направление вылета электрона Если пучек гамма-квантов попадает на атомы, то выбиваемые электроны вылетают преимущественно в направлении, перпендикулярном импульсу фотонов вдоль вектора электрического поля волны. Поэтому. угловое распределение фотоэлектронов для небольших энергий распределение для высокоэнергичных фотонов Фотоэффект - основной процесс поглощения фотонов при невысоких энергиях. Особенно эффективно поглощение на тяжелых атомах.
Cлайд 8
Комптон-эффект: энергия рассеянного фотона Упругое рассеяние γ-кванта высокой энергии на атомном электроне Энергия кванта много больше потенциала ионизации Еγ >> I ; электрон можно считать свободным В этом процессе γ-квант с энергией (волна - ) при рассеянии проявлял свойства частицы ( ) Выясним, как зависит энергия рассеянного кванта от угла рассеяния Сохранение 4-импульсов Получаем зависимость энергии рассеянного γ-кванта на угол в виде
Cлайд 9
Комптон-эффект: энергия рассеянного электрона Энергия рассеянного электрона в зависимости от угла его рассеяния и связь углов рассеянных частиц: электрона и γ-кванта При высокой энергии получается упрощенное выражение для энергии рассеянных гамма-квантов Энергия гамма-кванта после рассеяния не зависит от начальной энергии Для электрона Например, при рассеянии назад ( ) всегда энергия Такой результат - проявление корпускулярных свойств гамма-кванта
Cлайд 10
Сечение комптон-эффекта на электроне Для энергий фотонов соответствуют длины волн в области При низких энергиях ( Е < I ) длина волны значительно больше размеров атома. Прохождение э/м волны вызывает когерентные колебания атомных электронов под действием переменной составляющей электрического поля. Электроны переизлучают волну той же частоты (томсоновское рассеяние). Квантово-механическая формула Клейна-Нишины-Тамма для малых энергий сечение квази-линейно падает с ростом энергии гамма-квантов При больших энергиях
Cлайд 11
Сечение комптон-эффекта на протоне Возможен ли комптон-эффект на протоне? Качественное рассмотрение указывает, чтобы провзаимодействовать, гамма-квант должен “попасть в электромагнитную площадку” мишени , которая характеризуется комптоновской длиной волны частицы. Отсюда находим отношение Видно, что комптон-эффектом на протонах можно пренебречь. Аналогичный вывод получается из точных формул для сечения путем замены величины на значение в случае рассеяния на протоне. При взаимодействии гамма-квантов с веществом проявляются квантово-механические свойства микрообъектов
