X
Код презентации скопируйте его
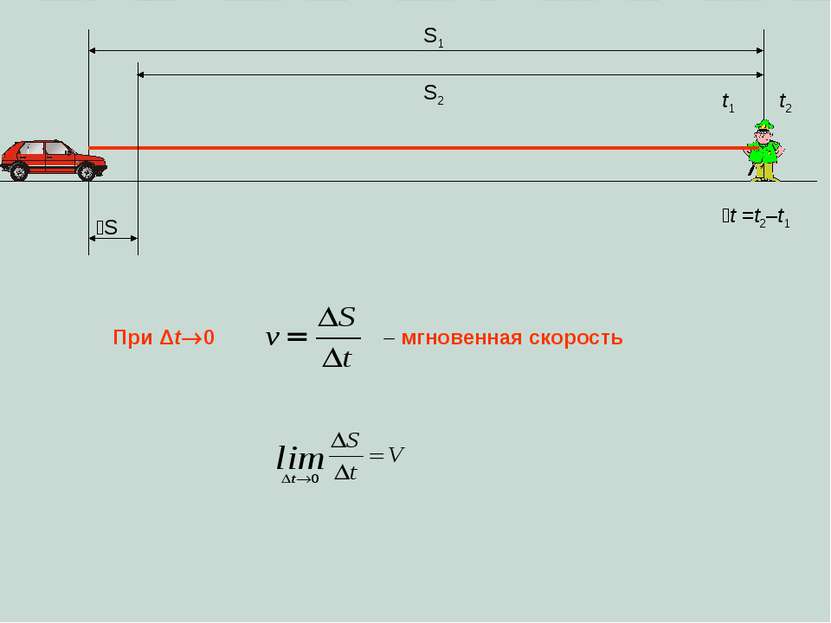
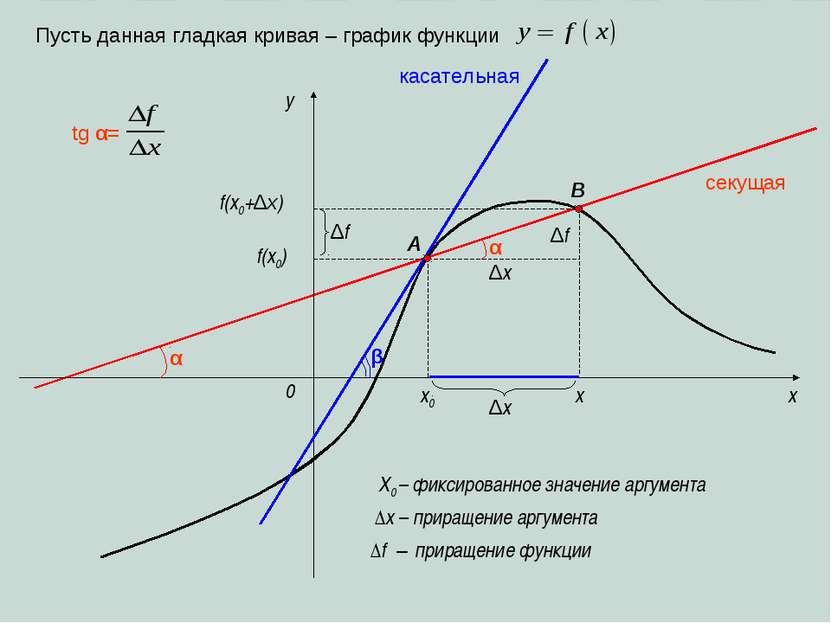
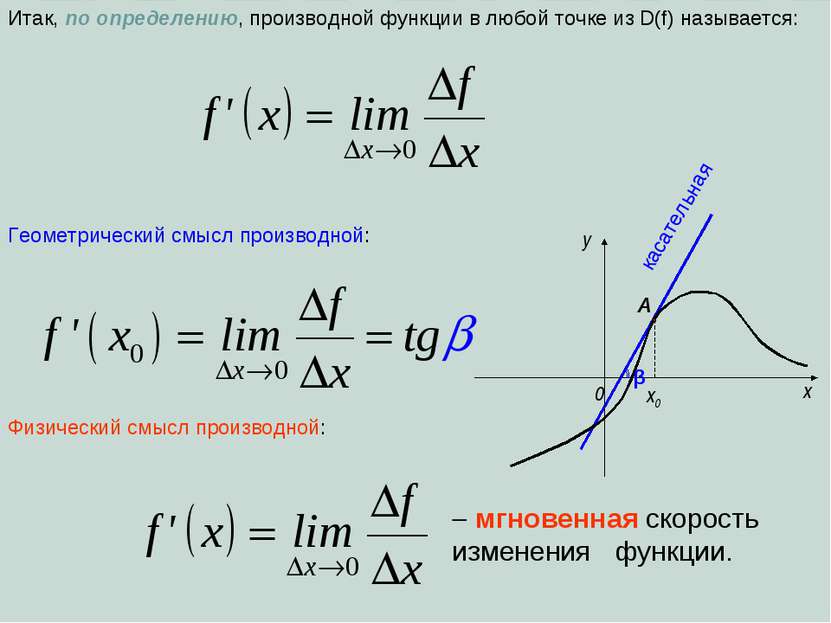
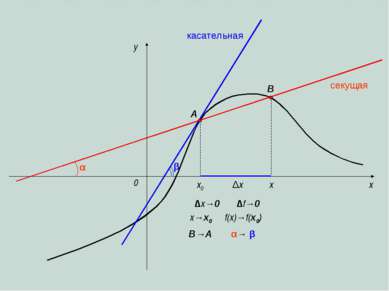
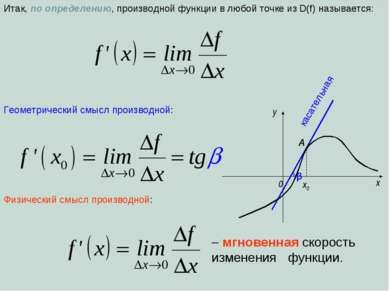
Определение производной функции y=f(x) в точке
Скачать эту презентацию
Презентация на тему Определение производной функции y=f(x) в точке
Скачать эту презентациюCлайд 1
Алгебра и начала анализа 10 класс ТЕМА: Определение производной функции в точке. Воробьев Леонид Альбертович, г.Минск
Cлайд 2
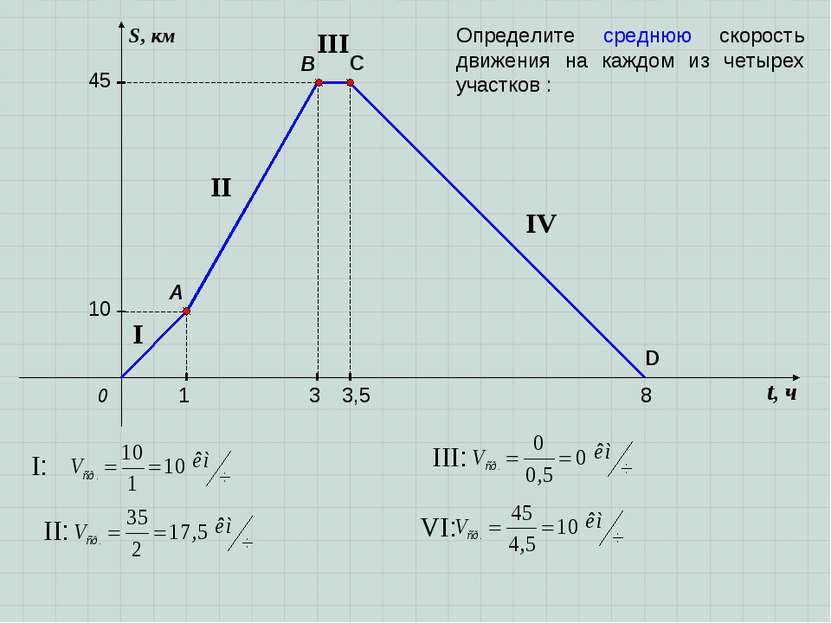
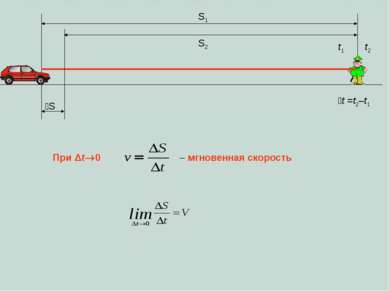
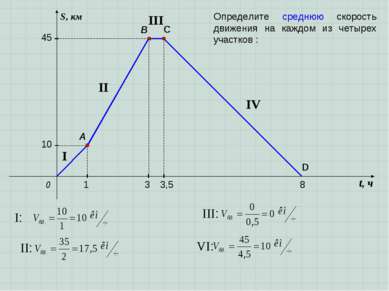t, ч S, км 0 A B 1 10 3 3,5 8 C 45 D I II III IV Определите среднюю скорость движения на каждом из четырех участков :
Cлайд 3
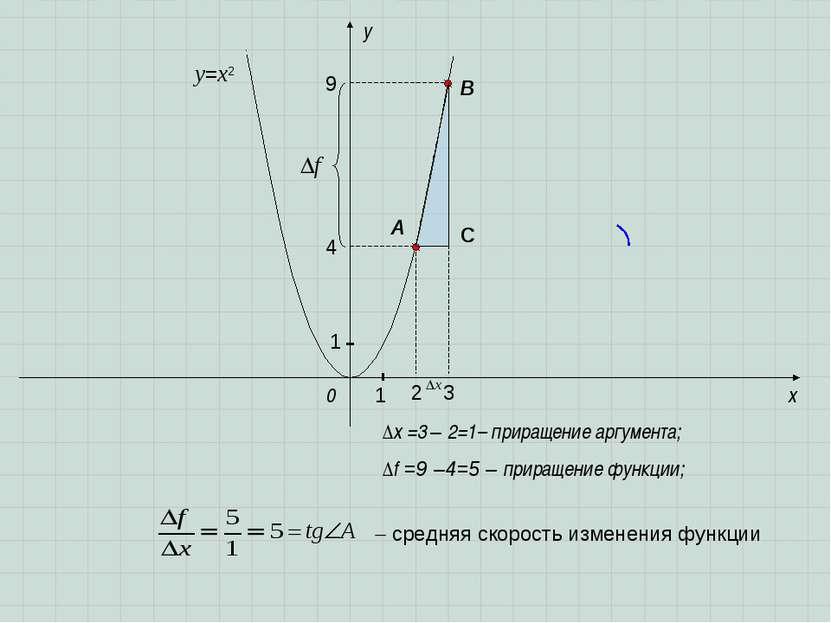
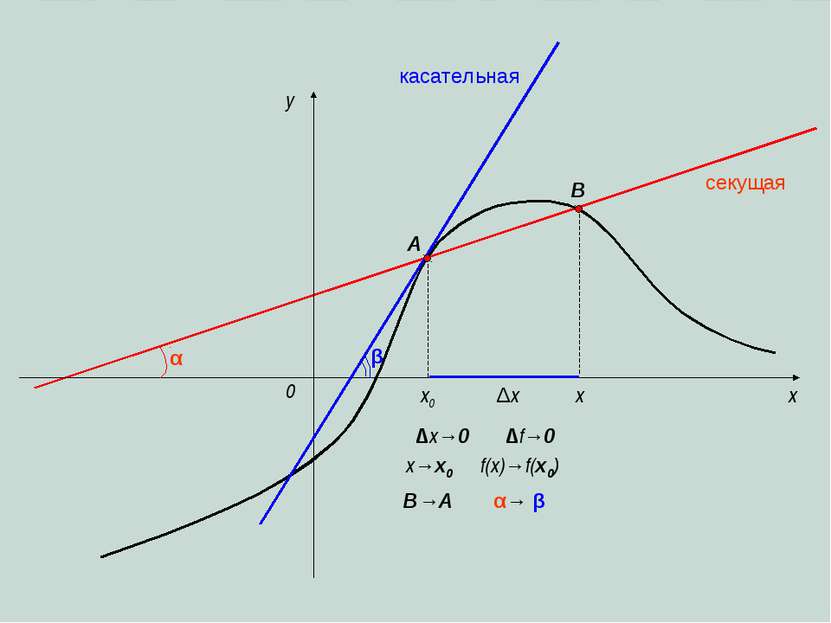
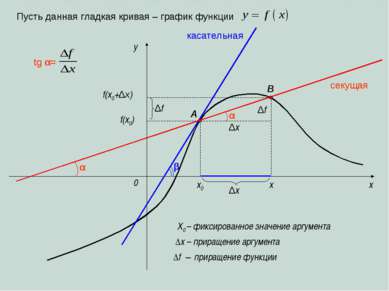
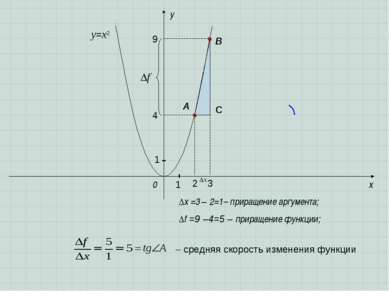x y 0 A B ∆f =9 –4=5 – приращение функции; ∆x =3 – 2=1– приращение аргумента; y=x2 1 1 9 4 2 3 C средняя скорость изменения функции
Cлайд 4
t1 t2 t =t2–t1 S1 S2 При Δt 0 мгновенная скорость
Cлайд 5
x y 0 x0 x ∆x секущая касательная Пусть данная гладкая кривая – график функции A B α β f(x0) f(x0+∆x) ∆f – приращение функции X0 – фиксированное значение аргумента ∆x – приращение аргумента ∆f α ∆x ∆f tg α=
Cлайд 6
x y 0 x0 x ∆x ∆x→0 x→x0 секущая касательная A B B→A β ∆f→0 α→ β α f(x)→f(x0)
Cлайд 7
Итак, по определению, производной функции в любой точке из D(f) называется: Геометрический смысл производной: Физический смысл производной: мгновенная скорость изменения функции.
