X
Код презентации скопируйте его
В6 элементы теории вероятностей
Скачать эту презентацию
Презентация на тему В6 элементы теории вероятностей
Скачать эту презентациюCлайд 1
В6 элементы теории вероятностей ГБОУ школа №255 Учитель математики Булатова Л.А.
Cлайд 2
Теоретические основы http://www.ege-study.ru/ege-materials/math/probability.html http://le-savchen.ucoz.ru/index/0-65 События Классическое определение вероятности Прототипы задач ЕГЭ 2013 с решениями http://mathege.ru
Cлайд 3
Немного о событиях Событие – все, что происходит или не происходит в реальной жизни. Случайное событие – событие, которое в ходе испытания (опыта) может произойти, а может и не произойти. Несовместные события – события, которые не могут произойти одновременно. Событие, противоположное событию А, состоит в том, что в результате испытания событие А не произошло. Обозначение: Ā
Cлайд 4
Вероятность Наступление того или иного случайного события происходит с некоторой вероятностью. Вероятностью P случайного события A называют отношение числа всех благоприятных исходов m испытания к общему числу n всех исходов Сумма вероятностей противоположных событий равна 1 Р(А) + Р(Ā) = 1
Cлайд 5
Например, бросают монету (проводят испытание). Возможны два случая (исхода): монета упала орлом (случайное событие), монета упала решкой (случайное событие). Эти события несовместные, так как одновременно монета выпасть орлом и решкой не может. Если монета не выпала орлом, значит, она выпала решкой. Эти события противоположные. Найдем вероятность того, что монета выпала орлом. Всего исходов n = 2, благоприятный исход (монета выпала орлом) m = 1. Р = 1/2 Вероятность того, что монета выпала решкой, определяется аналогично и равна ½. Так как события противоположные, то сумма вероятностей этих событий равна 1. 1/2 + ½ = 1
Cлайд 6
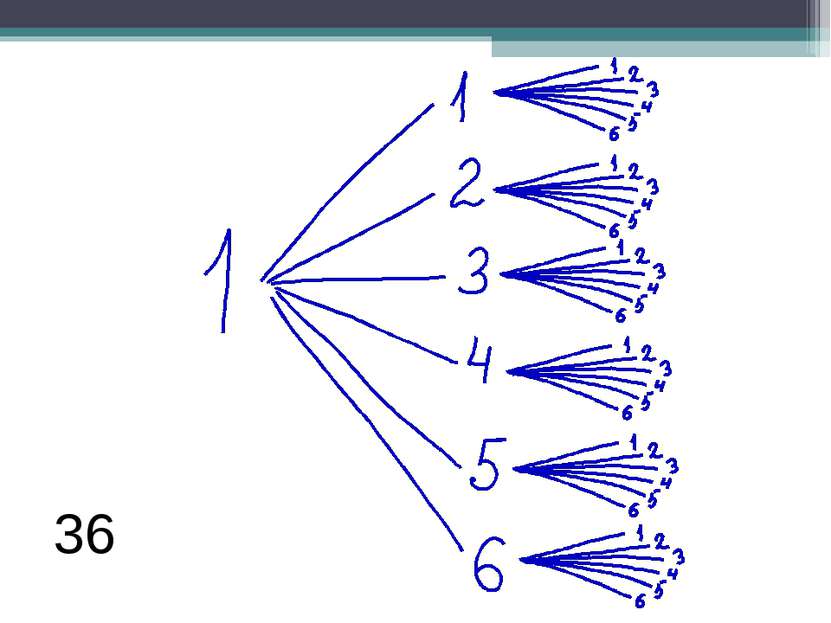
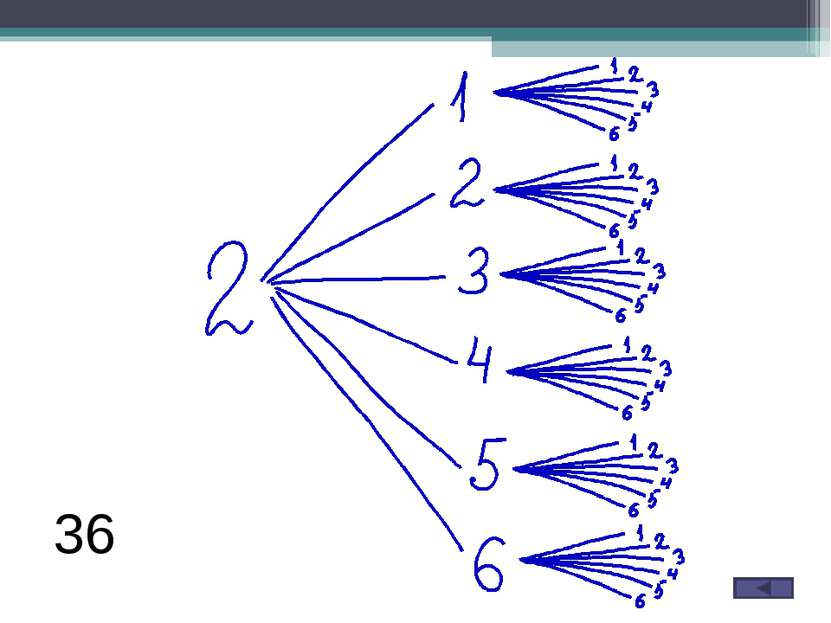
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение. В результате бросания первой кости возможны 6 исходов: выпадение 1, 2, 3, 4, 5, 6 очков. Для каждого из них возможны еще по шесть исходов при бросании второй кости. Общее количество исходов n= 6*6= 62=36 8 очков можно получить в следующих случаях : Количество благоприятных исходов m= 5 Вероятность по определению равна P = 5/36 = 0,138… ≈ 0,14 1 кость 2 кость 2 6 3 5 4 4 5 3 6 2
Cлайд 7
Задание B6 (№ 283443) В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых. Решение. Найдем общее количество исходов n. Для первой кости возможно 6 исходов – появление 1,2,3,4,5,6 очков, для каждого из которых по 6 при бросании второй и третьей кости, т.е. n = 6*6*6 = 63= 216 Найдем количество благоприятных исходов m. 16 очков можно получить следующими способами: 4 6 6 6 4 6 6 6 4 5 5 6 5 6 5 6 5 5 m = 6 Р = 6/216 =0,027… ≈ 0,03
Cлайд 8
36
Cлайд 9
36
Cлайд 10
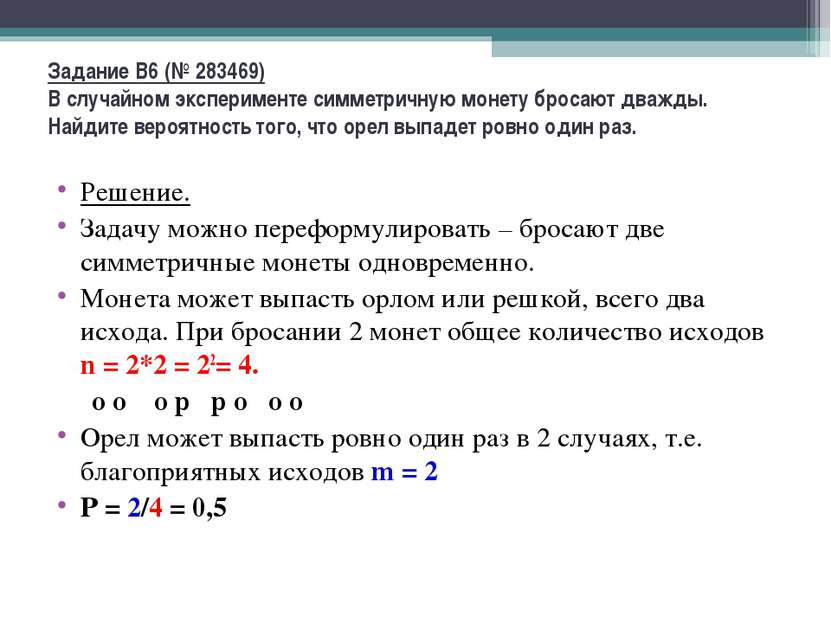
Задание B6 (№ 283469) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение. Задачу можно переформулировать – бросают две симметричные монеты одновременно. Монета может выпасть орлом или решкой, всего два исхода. При бросании 2 монет общее количество исходов n = 2*2 = 22= 4. о о о р р о о о Орел может выпасть ровно один раз в 2 случаях, т.е. благоприятных исходов m = 2 Р = 2/4 = 0,5
Cлайд 11
Задание B6 (№ 283467) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза. Решение. Задачу можно переформулировать – бросают три симметричные монеты одновременно. Монета может выпасть орлом или решкой, всего два исхода. При бросании 3 монет общее количество исходов n = 2*2*2 = 8. ооо оор оро орр роо рро рор ррр Орел может выпасть ровно два раза в 3 случаях, т.е. благоприятных исходов m = 3 Р = 3/8 = 0,375
Cлайд 12
Задание B6 (№ 283471) В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу. Решение. Общее количество исходов n = 2*2*2*2 = 24= 16. Орел не выпадет ни разу, если все 4 раза выпадет решка. Это возможно в одном случае, т.е. благоприятных исходов m = 1 Р = 1/16 = 0,0625
Cлайд 13
Задание B6 (№ 283479) В чемпионате по гимнастике участвуют 50 спортсменок: 24 из США, 13 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады. Решение. Общее количество спортсменок n = 50 Благоприятные исходы – спортсменка из Канады m = 50 – 24 - 13 = 13 P= 13/50 = 0, 26 Замечание. В данной задаче не учитывается, какой по счету окажется выступающая спортсменка
Cлайд 14
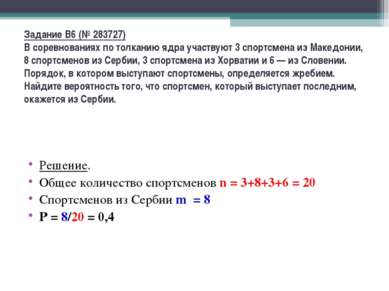Задание B6 (№ 283727) В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 8 спортсменов из Сербии, 3 спортсмена из Хорватии и 6 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Сербии. Решение. Общее количество спортсменов n = 3+8+3+6 = 20 Спортсменов из Сербии m = 8 Р = 8/20 = 0,4
Cлайд 15
Задание B6 (№ 286121) На семинар приехали 3 ученых из Швейцарии, 5 из Голландии и 4 из Франции. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что шестым окажется доклад ученого из Швейцарии. Решение аналогично предыдущей задачи Порядок выступления не учитывается при решении.
Cлайд 16
Задание B6 (№ 285929) Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 16 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Решение (аналогично) Общее количество докладов n = 40 На третий день запланировано (40-16):2=12 докладов, т.е. m = 12 P= 12/40 = 0,3
Cлайд 17
Задание B6 (№ 286211) Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 участников из России, в том числе Ярослав Исаков. Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким-либо теннисистом из России? Решение. Ярослав Исаков может сыграть в паре с любым из 46 - 1 = 45 участников. Т. е. n = 45 Среди них 19 - 1 = 18 пар, в которых Ярослав Исаков сыграет с теннисистом из России. Т.е. m = 18 Р = 18/45 = 0,4
Cлайд 18
Задание B6 (№ 286239) В сборнике билетов по математике всего 20 билетов, в 11 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам. Решение. Всего билетов n = 20 Вопрос по логарифмам содержится в 11 из них. m=11 Вероятность того, что вопрос по логарифмам достанется ученику равна Р=11/20=0,55
Cлайд 19
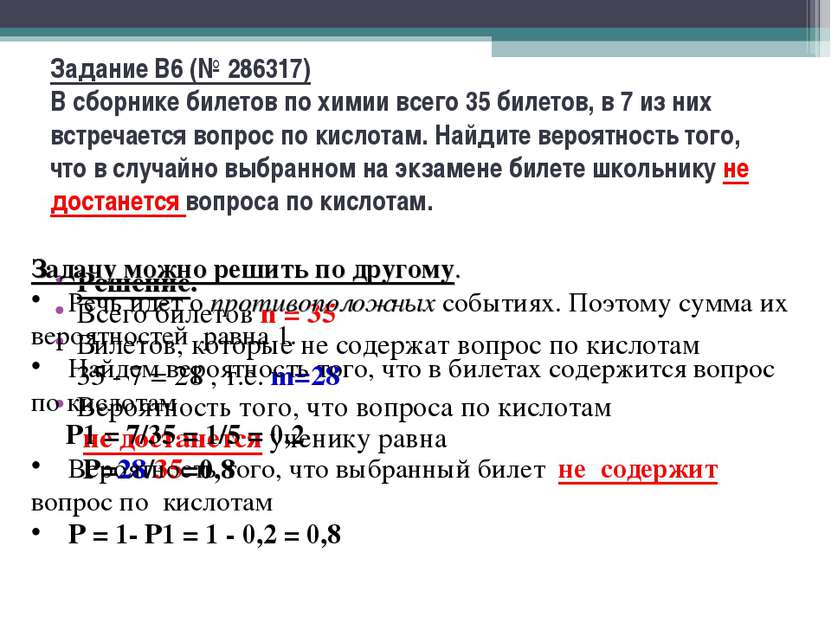
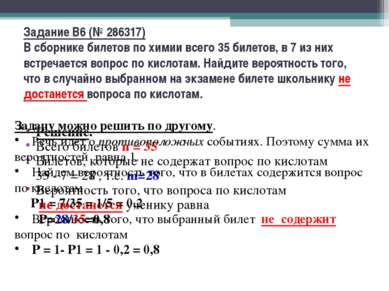Задание B6 (№ 286317) В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам. Решение. Всего билетов n = 35 Билетов, которые не содержат вопрос по кислотам 35 - 7 = 28 , т.е. m=28 Вероятность того, что вопроса по кислотам не достанется ученику равна Р=28/35=0,8 Задачу можно решить по другому. Речь идет о противоположных событиях. Поэтому сумма их вероятностей равна 1. Найдем вероятность того, что в билетах содержится вопрос по кислотам Р1 = 7/35 = 1/5 = 0,2 Вероятность того, что выбранный билет не содержит вопрос по кислотам Р = 1- Р1 = 1 - 0,2 = 0,8
Cлайд 20
Задание B6 (№ 283579) В среднем из 1400 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. Решение. Всего поступило в продажу насосов n = 1400 Насосов, которые не подтекают 1400 – 7 = 1393, т.е. m=1393 Вероятность того, что насос не подтекает равна Р=1393/1400=0,995 Задачу можно решить по другому. Речь идет о противоположных событиях. Поэтому сумма их вероятностей равна 1. Найдем вероятность того, что выбранный насос подтекает Р1 = 7/1400=1/200=0,005 Вероятность того, что выбранный насос не подтекает равна Р = 1- Р1 = 1 - 0,005 = 0,995
Cлайд 21
Задание B6 Фабрика выпускает сумки. В среднем из 120 сумок девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Решение. Всего сумок n = 120 Качественных сумок (благоприятные исходы) 111, т.е. m=120-9=111 Вероятность того, что сумка окажется качественной равна Р=111/120=0,925 Другой способ Р1 = 9/120 = 0,075 Р = 1 – 0,075 = 0,925
Cлайд 22
Задание B6 (№ 283633) Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решение. Всего сумок n = 120+9 = 129 Качественных сумок (благоприятные исходы) 120, т.е. m=120 Вероятность того, что сумка окажется качественной равна Р=120/129=0,930… ≈0,93
