X
Код презентации скопируйте его
ГИА 2013. Модуль АЛГЕБРА (№4)
Скачать эту презентацию
Презентация на тему ГИА 2013. Модуль АЛГЕБРА (№4)
Скачать эту презентациюCлайд 1
Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Cлайд 2
* Решите уравнение
Cлайд 3
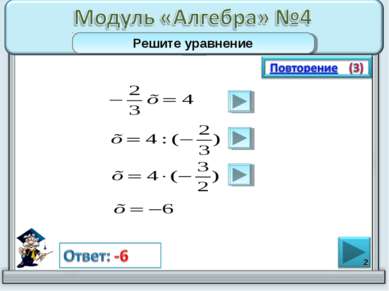
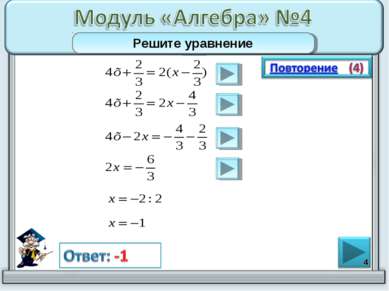
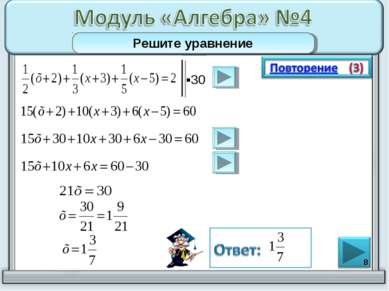
* В уравнении можно делить обе части уравнения на одно и то же число, не равное нулю. Чтобы разделить число на обыкновенную дробь, надо первое число умножить на взаимно обратное дроби. При умножении двух чисел в разными знаками результат будет отрицательным.
Cлайд 4
* Решите уравнение
Cлайд 5
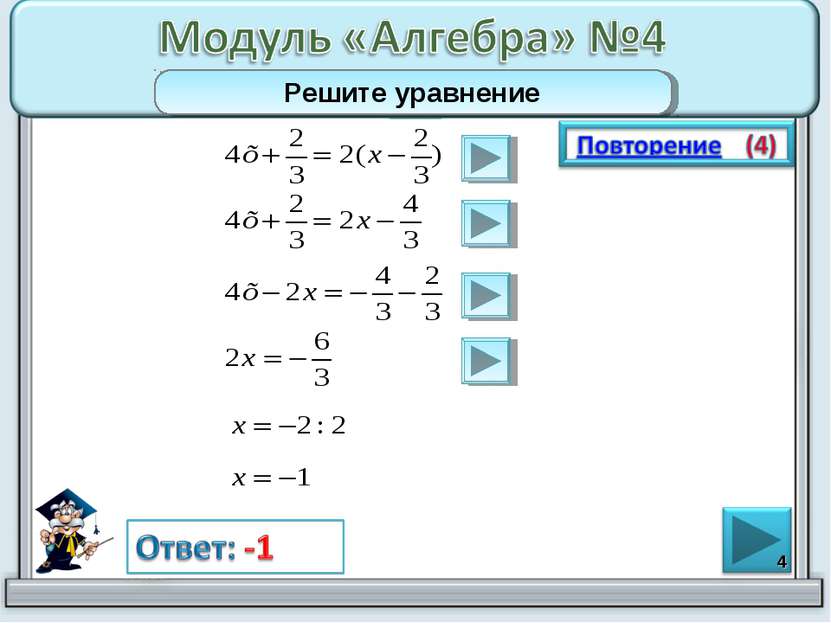
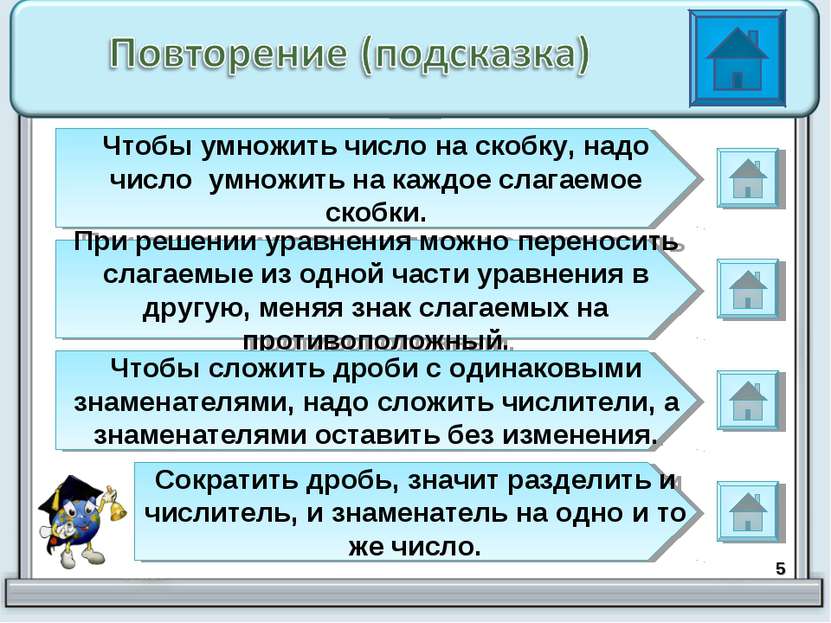
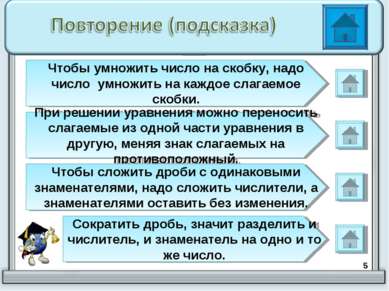* Чтобы умножить число на скобку, надо число умножить на каждое слагаемое скобки. При решении уравнения можно переносить слагаемые из одной части уравнения в другую, меняя знак слагаемых на противоположный. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить числители, а знаменателями оставить без изменения. Сократить дробь, значит разделить и числитель, и знаменатель на одно и то же число.
Cлайд 6
* Решите уравнение
Cлайд 7
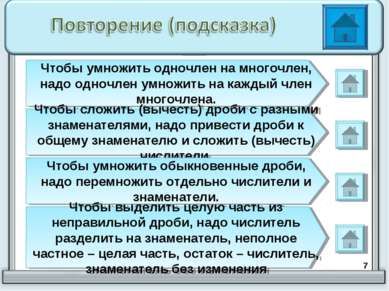* Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена. Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить (вычесть) числители. Чтобы умножить обыкновенные дроби, надо перемножить отдельно числители и знаменатели. Чтобы выделить целую часть из неправильной дроби, надо числитель разделить на знаменатель, неполное частное – целая часть, остаток – числитель, знаменатель без изменения
Cлайд 8
* Решите уравнение ▪30
Cлайд 9
* Чтобы «избавиться» от дробей, надо уравнение почленно умножить на общий знаменатель дробей, входящих в уравнение. Сумма противоположных чисел равна нулю. Подобными слагаемыми называются те, которые имеют одинаковую буквенную часть или не имеют ее вовсе.
Cлайд 10
▪(2-х), где 2-х≠0; х≠2 * Решите уравнение
Cлайд 11
* Дробно-рациональное уравнение имеет смысл тогда, когда знаменатель дробей, входящих в уравнение, не равен нулю. Дробно-рациональное уравнение можно свести к целому, если обе его части умножить на общий знаменатель.
Cлайд 12
* Решите уравнение Проверка: если х=-3,25, то верно
Cлайд 13
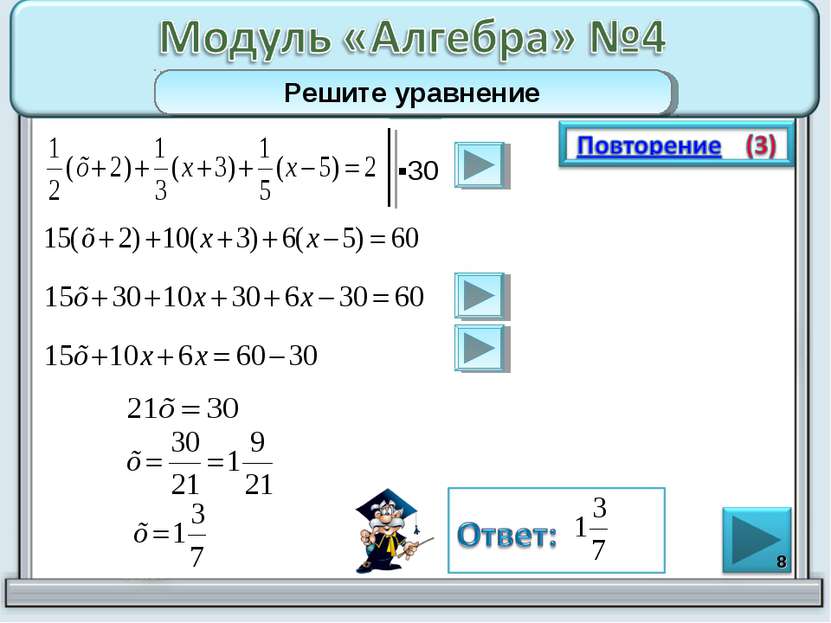
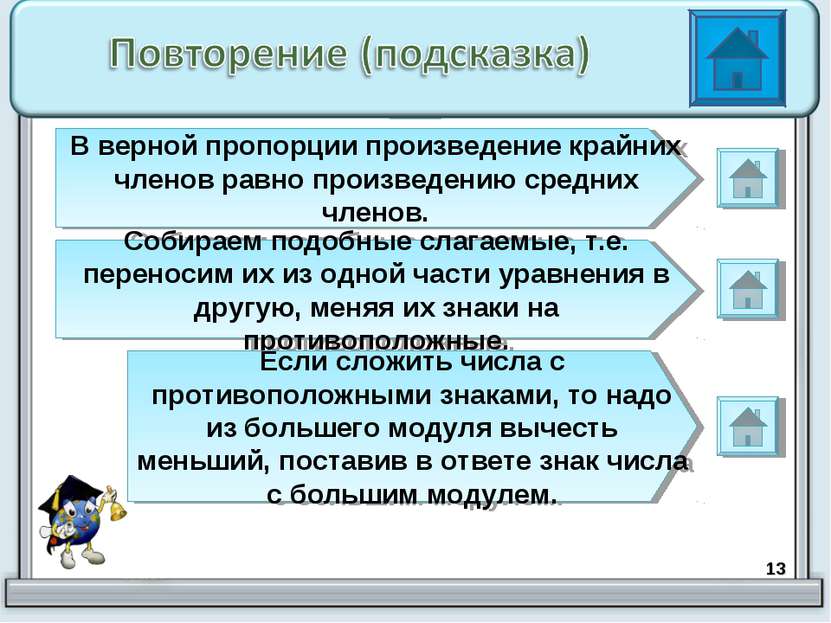
* В верной пропорции произведение крайних членов равно произведению средних членов. Собираем подобные слагаемые, т.е. переносим их из одной части уравнения в другую, меняя их знаки на противоположные. Если сложить числа с противоположными знаками, то надо из большего модуля вычесть меньший, поставив в ответе знак числа с большим модулем.
Cлайд 14
2 * Решите уравнение D>0, ⇒ 2 корня
Cлайд 15
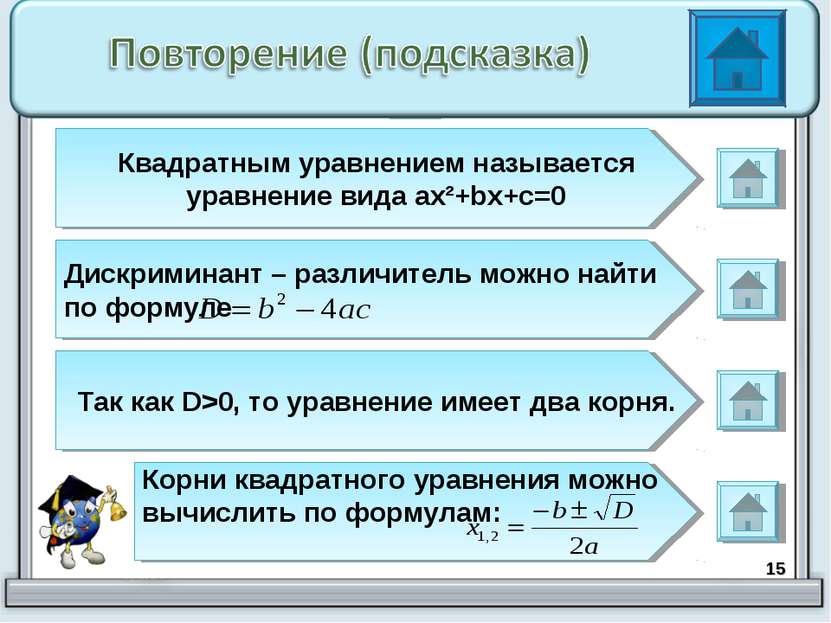
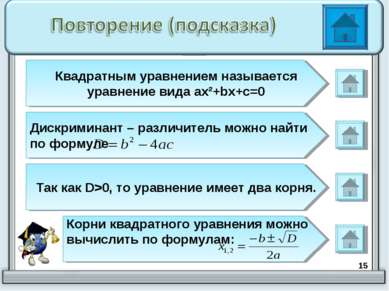* Квадратным уравнением называется уравнение вида ax²+bx+c=0 Дискриминант – различитель можно найти по формуле Так как D>0, то уравнение имеет два корня. Корни квадратного уравнения можно вычислить по формулам:
Cлайд 16
* Решите уравнение ⇒
Cлайд 17
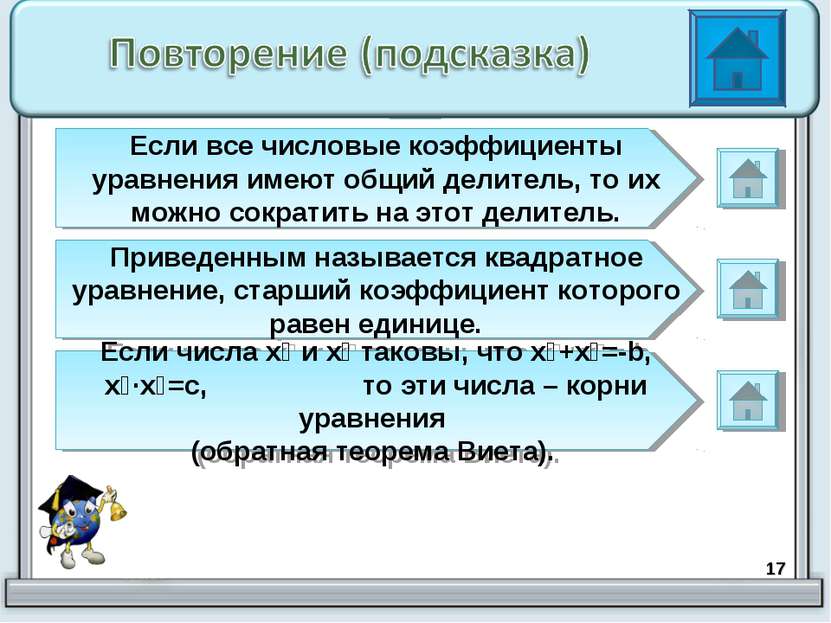
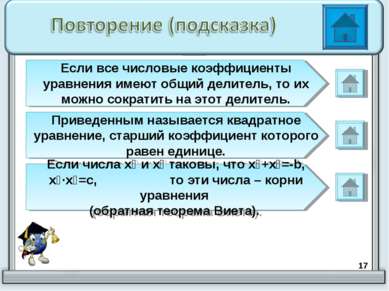* Если все числовые коэффициенты уравнения имеют общий делитель, то их можно сократить на этот делитель. Приведенным называется квадратное уравнение, старший коэффициент которого равен единице. Если числа х₁ и х₂ таковы, что х₁+х₂=-b, х₁∙х₂=с, то эти числа – корни уравнения (обратная теорема Виета).
Cлайд 18
Решим систему методом подстановки: * Решите систему уравнений
Cлайд 19
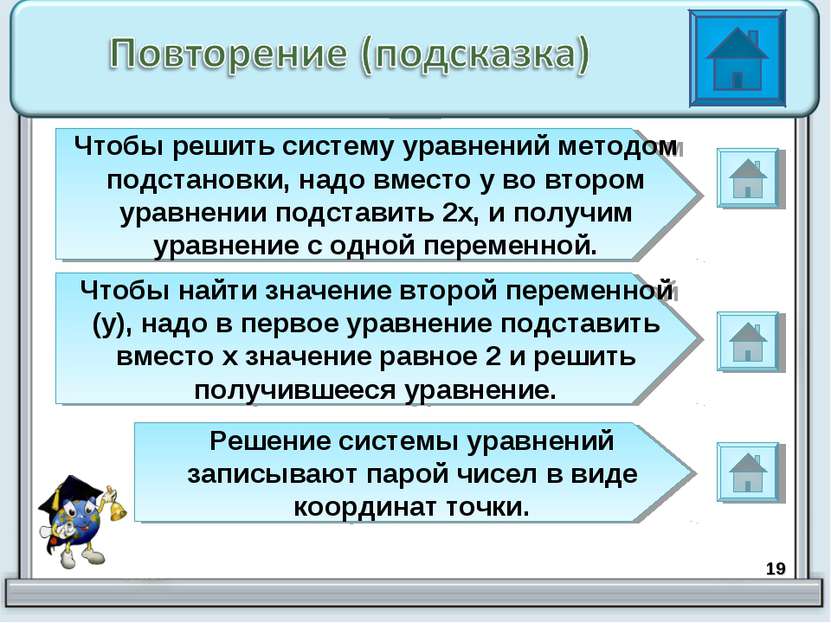
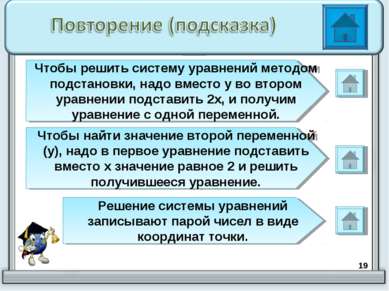* Чтобы решить систему уравнений методом подстановки, надо вместо у во втором уравнении подставить 2х, и получим уравнение с одной переменной. Чтобы найти значение второй переменной (у), надо в первое уравнение подставить вместо х значение равное 2 и решить получившееся уравнение. Решение системы уравнений записывают парой чисел в виде координат точки.
Cлайд 20
(-4) * Решите систему уравнений Решим систему методом сложения Уравнение не имеет решения
Cлайд 21
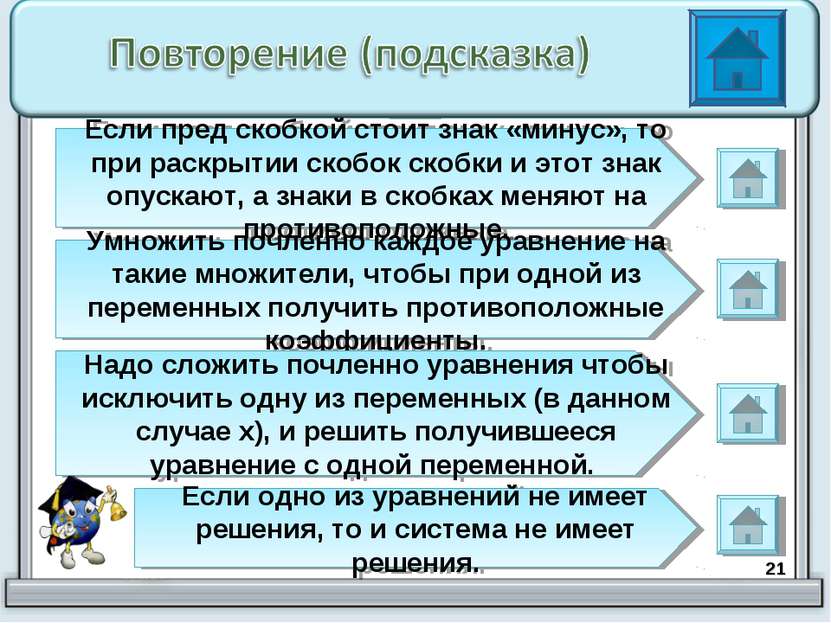
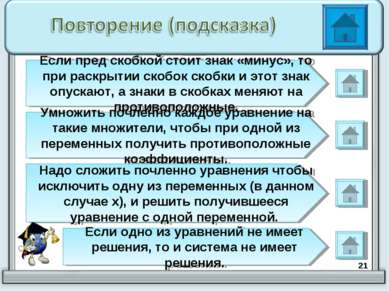* Если пред скобкой стоит знак «минус», то при раскрытии скобок скобки и этот знак опускают, а знаки в скобках меняют на противоположные. Умножить почленно каждое уравнение на такие множители, чтобы при одной из переменных получить противоположные коэффициенты. Надо сложить почленно уравнения чтобы исключить одну из переменных (в данном случае х), и решить получившееся уравнение с одной переменной. Если одно из уравнений не имеет решения, то и система не имеет решения.
Cлайд 22
http://krasdo.ucoz.ru/ee383358c499.png http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg Автор данного шаблона Ермолаева Ирина Алексеевна - учитель информатики и ИКТ (Муниципальное общеобразовательное учреждение «Павловская средняя общеобразовательная школа») http://narod.ru/disk/20305179001/SHabloni 2.rar.html «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013.
