X
Код презентации скопируйте его
Основы логики
Скачать эту презентацию
Презентация на тему Основы логики
Скачать эту презентациюCлайд 1
Морозова Инна Валентиновна Учитель информатики и технологии МБОУ»СОШ №3 им. Г.В.Зимина» г. Калуги
Cлайд 2
Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Cлайд 3
Джордж Буль
Cлайд 4
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Cлайд 5
Пример: «Трава зеленая» -истинное высказывание. «Лев – птица» - ложное высказывание.
Cлайд 6
Не всякое предложение является логическим высказыванием. Пример: «ученик десятого класса» «информатика — интересный предмет».
Cлайд 7
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Cлайд 8
Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Cлайд 9
Пример: Элементарные высказывания: «Петров — врач», «Петров — шахматист» Составные высказывания: "Петров — врач и шахматист", понимаемое как "Петров — врач, хорошо играющий в шахматы". "Петров — врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".
Cлайд 10
Чтобы обращаться к логическим высказываниям, их обозначают буквами. Пример: А = «Луна – спутник Земли», А = 1 В = « 3* 2 = 5», В = 0
Cлайд 11
Пример: А ="Тимур поедет летом на море", В = "Тимур летом отправится в горы". А и В = "Тимур летом побывает и на море, и в горах»
Cлайд 12
Операции над логическими высказываниями
Cлайд 13
Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Cлайд 14
Логическое «отрицание» (инверсия или НЕ) обозначается чертой над высказыванием Ā .
Cлайд 15
Диаграмма Эйлера-Венна:
Cлайд 16
Пример: А = «Луна — спутник Земли» А = "Луна — не спутник Земли"
Cлайд 17
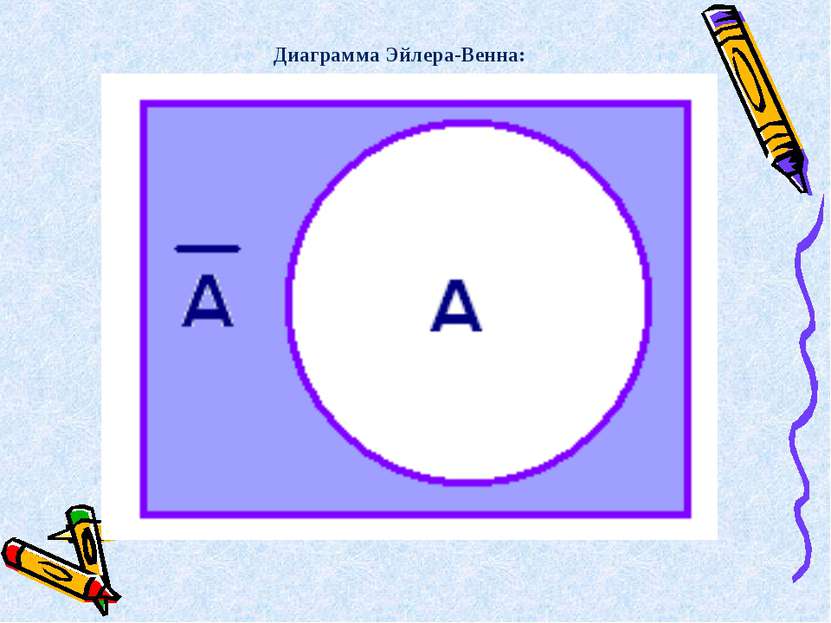
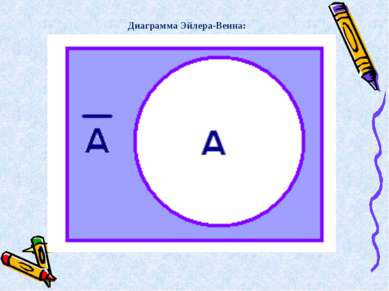
Высказывание А истинно, когда A ложно, и ложно, когда A истинно. Таблица истинности А А 0 1 1 0
Cлайд 18
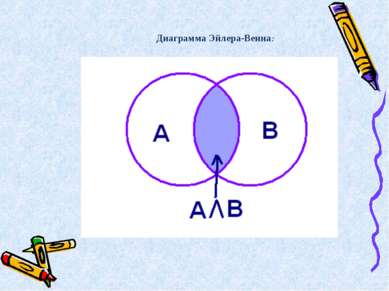
Логическое умножение ( «и», конъюнкция (лат. conjunctio — соединение)) обозначается точкой " . " (может также обозначаться знаками /\ или &). А . В, А /\ В, А & В
Cлайд 19
Диаграмма Эйлера-Венна:
Cлайд 20
Пример: А = «10 делится на 2», А= 1 В = «5 больше 3», В = 1 С = « 4 – нечётное число», С = 0 А & В = «10 делится на 2 и 5 больше 3», А & В = 1 А & С = «10 делится на 2 и 4 – чётное число», А & С = 0
Cлайд 21
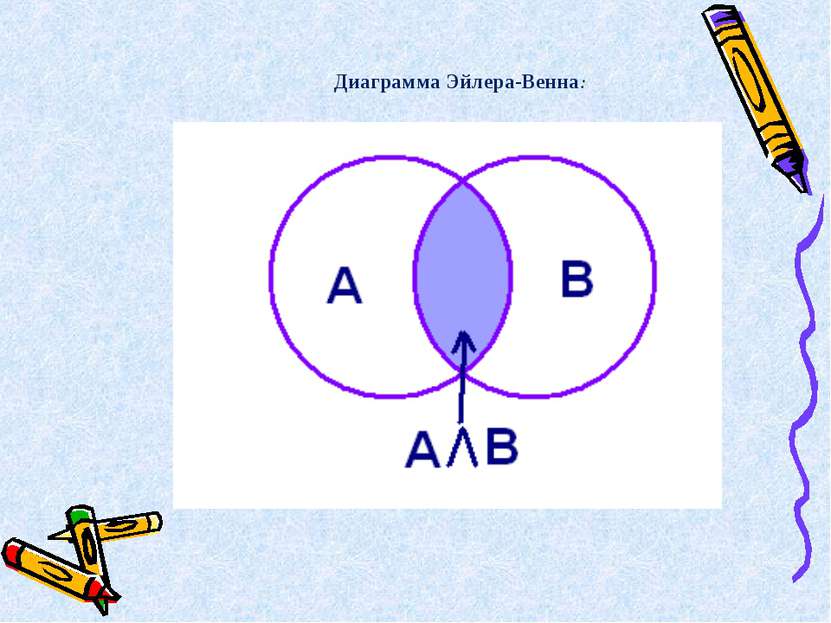
Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны. Таблица истинности X Y X&Y 0 0 0 1 0 0 0 1 0 1 1 1
Cлайд 22
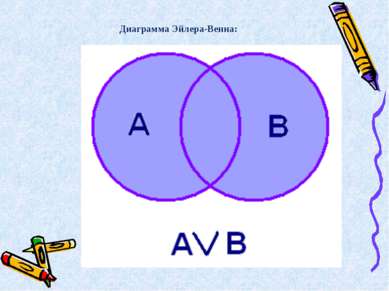
Логическое сложение ( «или», дизъюнкция (лат. disjunctio — разделение) обозначается знаком v или +. А V В, А + В
Cлайд 23
Диаграмма Эйлера-Венна:
Cлайд 24
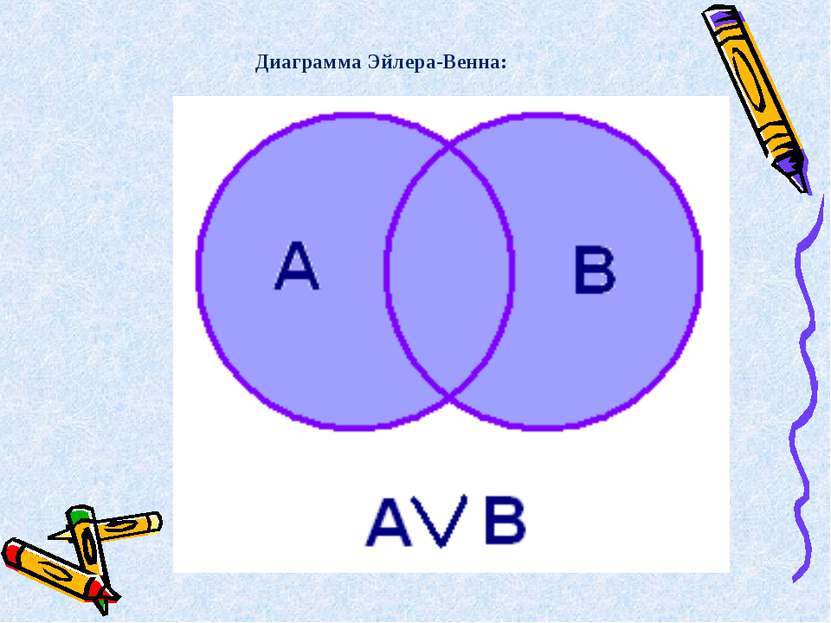
Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Таблица истинности X Y X+Y 0 0 0 1 0 1 0 1 1 1 1 1
Cлайд 25
Импликация (лат. implico — тесно связаны) -операция, выражаемая связками «если ..., то…», «из ... следует…», «... влечет ...». Обозначается знаком . А В .
Cлайд 26
Высказывание А В ложно тогда и только тогда, когда А истинно, а В – ложно. Таблица истинности А В А В 0 0 0 0 1 1 1 0 1 1 1 1
Cлайд 27
Эквиваленция (двойная импликация) - операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно ...» Обозначается знаком или ~. А В, А ~ В.
Cлайд 28
Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают. Таблица истинности А В А В 0 0 1 0 1 0 1 0 0 1 1 1
Cлайд 29
А = «10 делится на 2», А= 1 В = «5 больше 3», В = 1 С = « 4 – нечётное число», С = 0 К = « 3 – чётное число», К = 0 А + В = «10 делится на 2 или 5 больше 3», А + В = 1 А + С = «10 делится на 2 или 4 – чётное число», А + С = 1 С + К = « 4 – нечётное число или 3 – чётное число», С+К = 0 Пример:
Cлайд 30
Порядок выполнения логических операций 1.Сначала выполняется операция отрицания (“не”), 2. Затем конъюнкция (“и”), 3. После конъюнкции — дизъюнкция (“или”), 4. В последнюю очередь — импликация и эквиваленция.
Cлайд 31
A → B = ¬ A B Законы де Моргана ¬ (A B) = ¬ A ¬ B ¬ (A B) = ¬ A ¬ B 3. Законы коммутативности А&B B&A AVB BVA 4. Законы ассоциативности (А&B)&C A&(B&C) (АVB)VC AV(BVC) 5. Законы дистрибутивности А&(BVC) (A&B)V(A&C) АV(B&C) (AVB)&(AVC) 6. Законы поглощения A&(AVB) A AV(A&B) A 7. Законы противоречия A&¬A=0 8. Закон исключения третьего AV¬A=1 9. Закон двойного отрицания ¬¬A=A 10. Закон контрапозиции A-›B ¬A->¬B Законы логики.
Cлайд 32
http://electrik.info/main/fakty/229-buleva-algebra-chast-1-nemnogo-istorii.html http://booleanalgebra.narod.ru/ http://www.mirea.ac.ru/d1/metodika/Indexmet.htm http://alglib.sources.ru/articles/logic.php http://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D00 http://www.sch861.ru/2-school/3-11-ikt/ikt/urok/logica/2.html· http://kpolyakov.narod.ru/school/ege.htm О.Б. Богомолова Логические задачи. — М. БИНОМ. Лаборатория знаний, 2005 В.Ю. Лыскова, Е.А. Ракитина Логика в информатике. — М. “Информатика и образование”. 1999 г. С.С. Коробков Элементы математической логики и теории вероятности. — Екатеринбург, 1999 М.И. Башмаков Уроки математики. Выпуск 4. Учимся логике. — Санкт-Петербург “Информатизация образования”, 2000 г. А.П. Бойко Практикум по логике. — М. “Издательский центр АЗ”, 1997 г. А.С. Жилин Логические задачи. Список использованных источников информации.
