X
Код презентации скопируйте его
Основы логики Алгебра высказываний
Скачать эту презентацию
Презентация на тему Основы логики Алгебра высказываний
Скачать эту презентациюCлайд 1
Основы логики Алгебра высказываний Автор: Сергеев Евгений Викторович МОУ СОШ №4 г. Миньяра Челябинской области sergeev73@mail.ru http://shk4-minyar.ucoz.ru
Cлайд 2
Алгебра высказываний Алгебра высказываний была разработана для того, чтобы определять истинность или ложность составных высказываний, не вникая в их содержание
Cлайд 3
Логические переменные Логические переменные – простые высказывания, содержащие только одну мысль. Обозначаются буквами латинского алфавита: A, B, C… Логические переменные могут принимать лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)
Cлайд 4
Логические переменные Например, два простых высказывания: А = «2 2 = 4» истина (1) В = «2 2 = 5» ложь (0) являются логическими переменными А и В
Cлайд 5
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)
Cлайд 6
В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные логические операции, в результате которых получаются новые высказывания
Cлайд 7
Составные высказывания Высказывания, состоящие из нескольких простых суждений и содержащие в себе более, чем одну простую мысль, называются логическими функциями Обозначаются F(A,B,C…) Также могут принимать значения «ИСТИНА» или «ЛОЖЬ» в зависимости от того, какие значения имеют входящие в их состав логические переменные и от действий над ними
Cлайд 8
Логические операции Конъюнкция (логическое умножение, «И») Дизъюнкция (логическое сложение, «ИЛИ») Инверсия (логическое отрицание, «НЕ») Импликация (логическое следование, «Если А, то В») Эквивалентность (логическое равенство, «А тогда и только тогда, когда В»)
Cлайд 9
Объединение двух или нескольких высказываний в одно с помощью союза «И» называется операцией логического умножения, или конъюнкцией
Cлайд 10
Логическая функция, полученная в результате конъюнкции, истинна тогда и только тогда, когда истинны все входящие в него логические переменные
Cлайд 11
Конъюнкция. Определите истинность логической функции «2 2 = 5» И «3 3 = 10» «2 2 = 5» И «3 3 = 9» «2 2 = 4» И «3 3 = 10» «2 2 = 4» И «3 3 = 9» Истинна только функция (4)
Cлайд 12
Запись конъюнкции на формальном языке алгебры высказываний F(A,B) = A & B или F(A,B) = A B Также может встретиться запись, типа: F(A,B) = A * B или F(A,B) = A and B
Cлайд 13
Значение логической функции определяется по ее таблице истинности Таблица истинности показывает какие значения принимает логическая функция при всех возможных значениях логических переменных
Cлайд 14
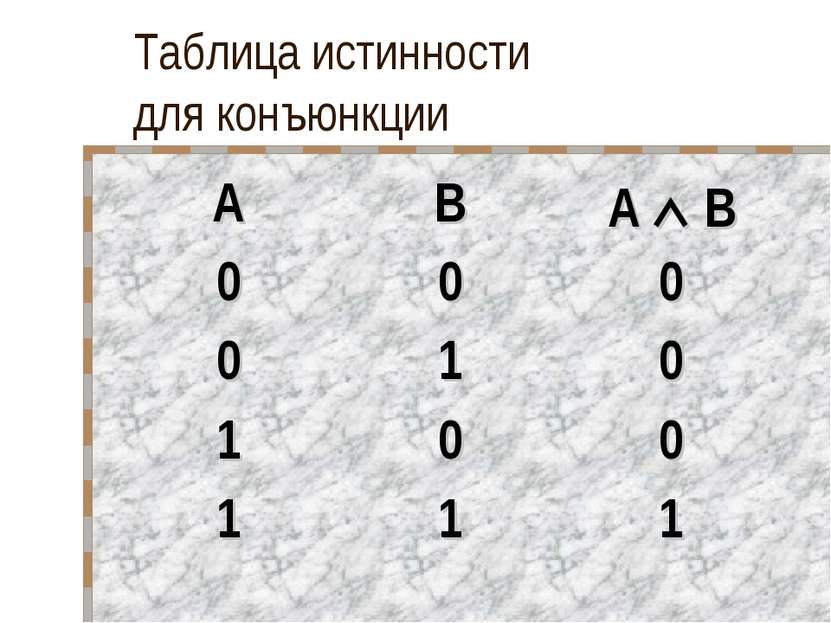
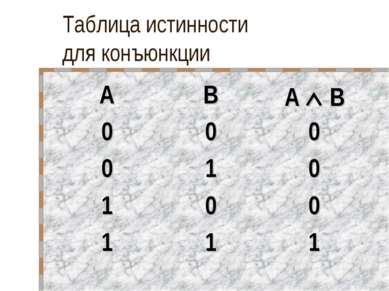
Таблица истинности для конъюнкции A B A B 2 2 = 5 3 3 = 10 ЛОЖЬ 2 2 = 5 3 3 = 9 ЛОЖЬ 2 2 = 4 3 3 = 10 ЛОЖЬ 2 2 = 4 3 3 = 9 ИСТИНА
Cлайд 15
Таблица истинности для конъюнкции A B A B 0 0 0 0 1 0 1 0 0 1 1 1
Cлайд 16
Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения, или дизъюнкцией
Cлайд 17
Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя бы одна из входящих в него логических переменных
Cлайд 18
Дизъюнкция. Определите истинность логической функции «2 2 = 5» ИЛИ «3 3 = 10» «2 2 = 5» ИЛИ «3 3 = 9» «2 2 = 4» ИЛИ «3 3 = 10» «2 2 = 4» ИЛИ «3 3 = 9» Ложна только функция (1), остальные истинны
Cлайд 19
Запись дизъюнкции на формальном языке алгебры высказываний F(A,B) = A B Также может встретиться запись, типа: F(A,B) = A + B или F(A,B) = A or B
Cлайд 20
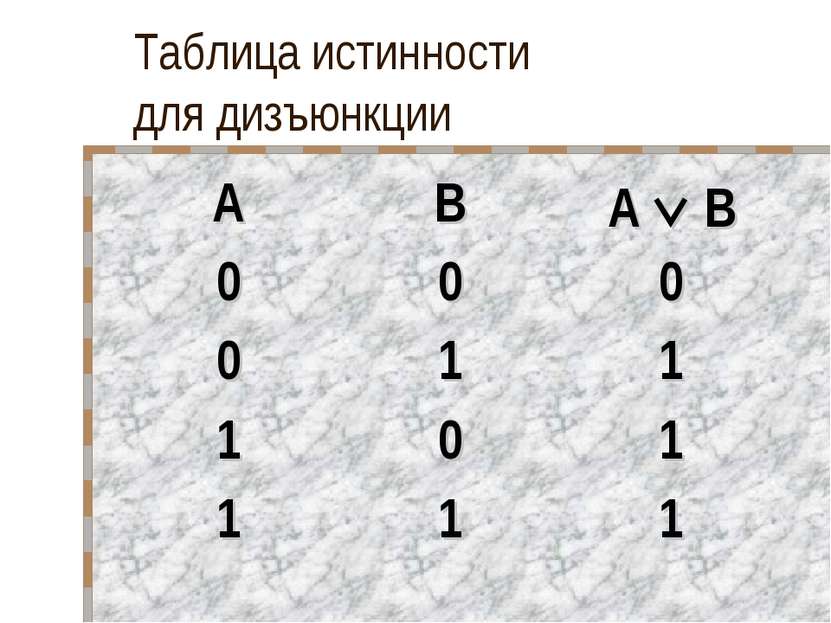
Таблица истинности для дизъюнкции A B A B 2 2 = 5 3 3 = 10 ЛОЖЬ 2 2 = 5 3 3 = 9 ИСТИНА 2 2 = 4 3 3 = 10 ИСТИНА 2 2 = 4 3 3 = 9 ИСТИНА
Cлайд 21
Таблица истинности для дизъюнкции A B A B 0 0 0 0 1 1 1 0 1 1 1 1
Cлайд 22
Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией
Cлайд 23
Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]
Cлайд 24
Инверсия Пусть A = «2 2 = 4» – истинное высказывание, тогда F(A) = «2 2 ≠ 4» – ложное высказывание
Cлайд 25
Запись инверсии на формальном языке алгебры высказываний F(A) = ¬A или F(A) = Ā Также может встретиться запись, типа: F(A) = not А
Cлайд 26
Таблица истинности для инверсии А ¬А 0 1 1 0
Cлайд 27
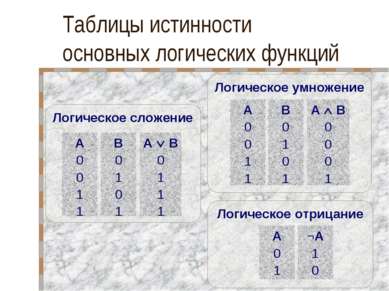Таблицы истинности основных логических функций Логическое умножение A 0 0 1 1 B 0 1 0 1 A B 0 0 0 1 Логическое сложение Логическое отрицание A 0 1 ¬A 1 0 A 0 0 1 1 B 0 1 0 1 А В 0 1 1 1
Cлайд 28
Дополнительные логические функции Импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание, поэтому их называют дополнительными логическими функциями: Импликация: А → В = ¬A В или А В = ¬A В или А В = ¬A В Эквивалентность: А ↔ В = (¬A В) (¬B A) или А В = (¬A В) (¬B A) или А ≡ В = (¬A В) (¬B A)
Cлайд 29
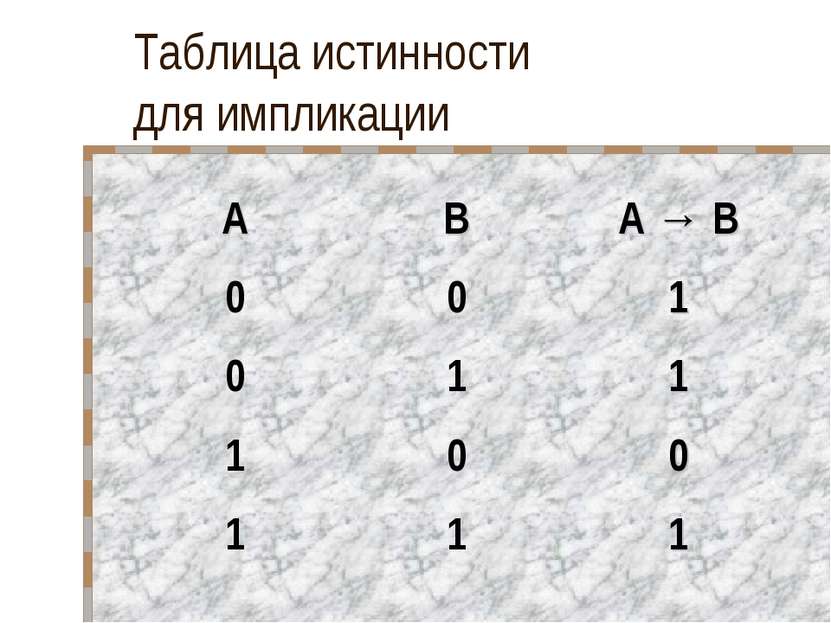
Импликация Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется импликацией (логическим следованием)
Cлайд 30
Импликация Импликация ложна тогда и только тогда, когда условие истинно, а следствие ложно Пример: Если выучишь материал, то сдашь зачет Это высказывание ложно только тогда, когда материал выучен, а зачет не сдан, т.к. сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой
Cлайд 31
Таблица истинности для импликации A B A → B 0 0 1 0 1 1 1 0 0 1 1 1
Cлайд 32
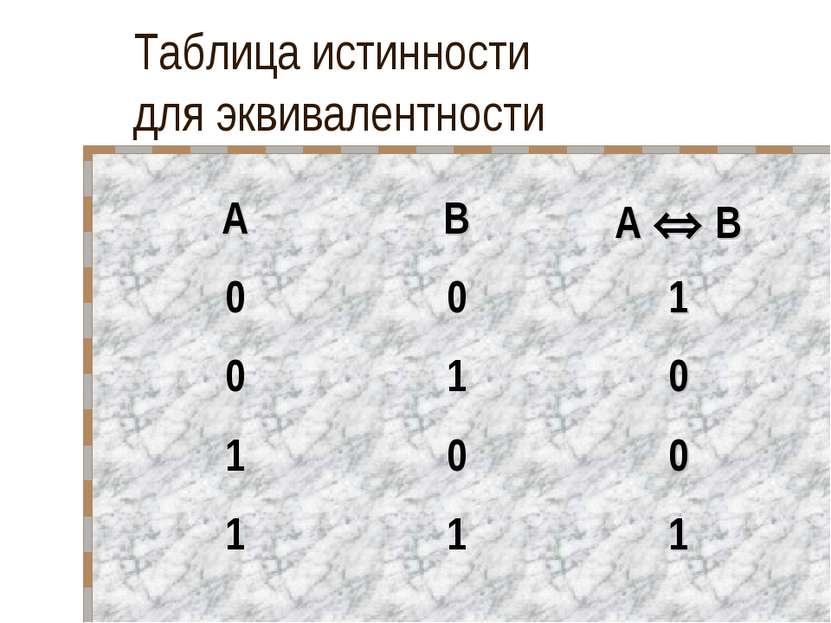
Эквивалентность Эквивалентность – это логическая операция, объединяющая два простых высказывания в одно составное и которое является истинным тогда и только тогда, когда оба исходных высказывания одновременно либо истинны, либо ложны.
Cлайд 33
Таблица истинности для эквивалентности A B A B 0 0 1 0 1 0 1 0 0 1 1 1
Cлайд 34
Переместительный Дизъюнкция: X Y ≡ Y X Конъюнкция: X Y ≡ Y X Основные законы алгебры высказываний
Cлайд 35
Сочетательный Дизъюнкция: X (Y Z) ≡ (X Y) Z Конъюнкция: X (Y Z) ≡ (X Y) Z Основные законы алгебры высказываний
Cлайд 36
Распределительный Дизъюнкция: X (Y Z) ≡ X Y X Z Конъюнкция: X (Y Z) ≡ (X Y) (X Z) Основные законы алгебры высказываний
Cлайд 37
Правила де Моргана Дизъюнкция: ¬(X Y) ≡ ¬X ¬Y Конъюнкция: ¬(X Y) ≡ ¬X ¬Y Основные законы алгебры высказываний
Cлайд 38
Идемпотенции Дизъюнкция: X X ≡ X Конъюнкция: X X ≡ X Основные законы алгебры высказываний
Cлайд 39
Поглощения Дизъюнкция: X (X Y) ≡ X Конъюнкция: X (X Y) ≡ X Основные законы алгебры высказываний
Cлайд 40
Склеивания Дизъюнкция: (X Y) (¬X Y) ≡ Y Конъюнкция: (X Y) (¬X Y) ≡ Y Основные законы алгебры высказываний
Cлайд 41
Переменная со своей инверсией Дизъюнкция: X ¬X ≡ 1 Конъюнкция: X ¬X ≡ 0 Основные законы алгебры высказываний
Cлайд 42
Операция с константами Дизъюнкция: X 0 ≡ X, X 1 ≡ 1 Конъюнкция: X 0 ≡ 0, X 1 ≡ X Основные законы алгебры высказываний
Cлайд 43
Двойного отрицания ¬(¬X) ≡ X Основные законы алгебры высказываний
Cлайд 44
Порядок действий Действия в скобках Отрицание Конъюнкция Дизъюнкция Импликация Эквивалентность
