Войти
X

Код презентации скопируйте его

Ширина px

Вы можете изменить размер презентации, указав свою ширину плеера!

Двугранные углы

Скачать эту презентацию

Получить код Увеличить
Рассмотрим два полупространства , образованных непараллельными плоскостями Пе... Прямую , по которой пересекаются плоскости – границы полупространств , называ... Двугранный угол с гранями , β ребром а обозначают а β. Можно использовать и т... Для измерения двугранного угла введём понятие его линейного угла. На ребре а ... а β О А В Так как ОА а ,ОВ а , то плоскость АОВ перпендикулярна прямой а . γ ... Теорема : Величина линейного угла не зависит от выбора его вершины на ребре д... Двугранный угол является острым , прямым или тупым , если его линейный угол с... Двугранный угол является острым , прямым или тупым , если его линейный угол с... Двугранный угол является острым , прямым или тупым , если его линейный угол с... Заметим , что аналогично тому , как и на плоскости , в пространстве определяю... Заметим , что аналогично тому , как и на плоскости , в пространстве определяю... Определение : Углом между двумя пересекающимися плоскостями называется наимен... β β1 а 1 с Величина угла между плоскостями принадлежит промежутку [0°;90°]. Учебник “ГЕОМЕТРИЯ 10 класс” Е.В.Потоскуев , Л.И. Звавич §14
1 15

Презентация на тему Двугранные углы

Скачать эту презентацию

Cлайд 1
Cлайд 2
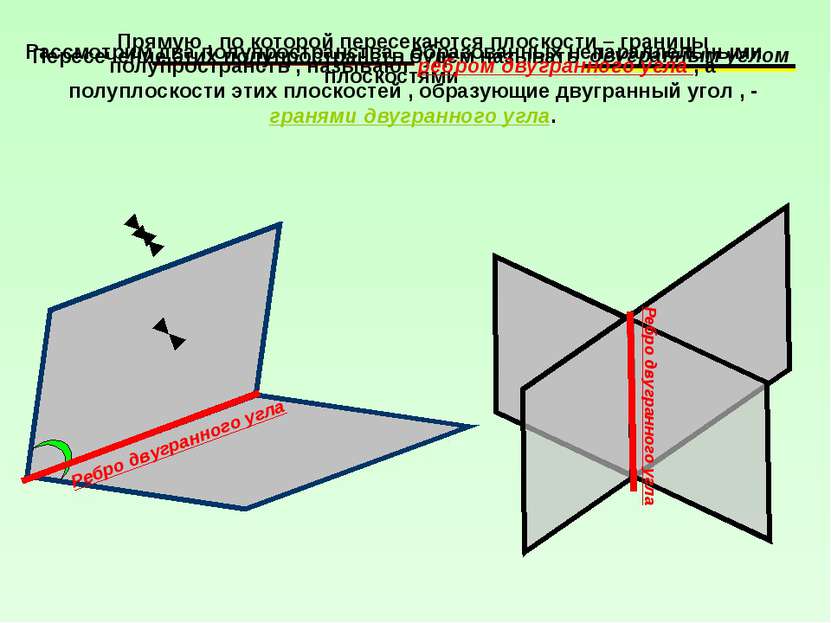
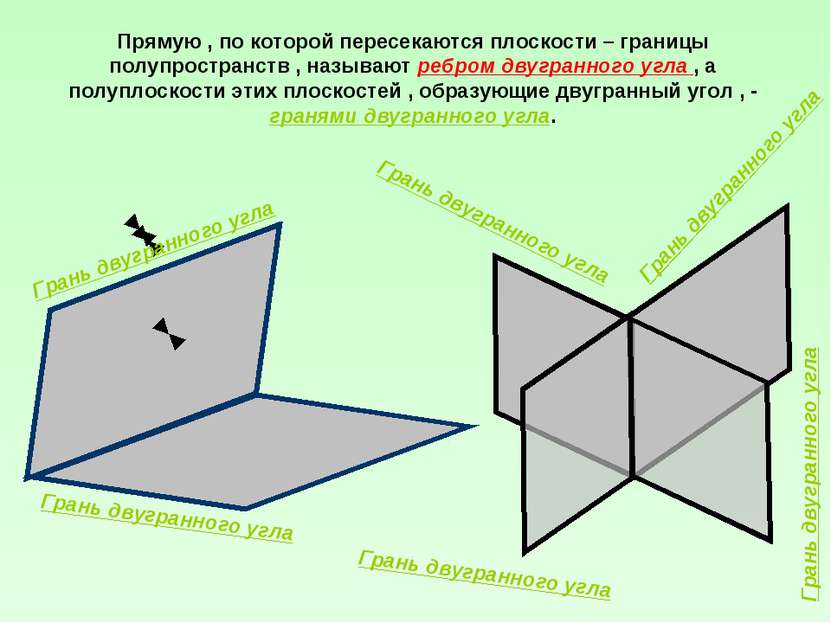
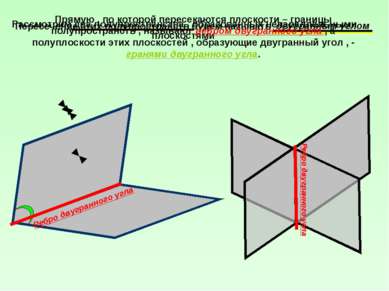Рассмотрим два полупространства , образованных непараллельными плоскостями Пе... Рассмотрим два полупространства , образованных непараллельными плоскостями Пересечение этих полупространств будем называть двугранным углом Прямую , по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла. Ребро двугранного угла Ребро двугранного угла
Cлайд 3
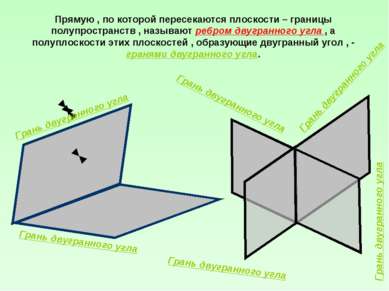Прямую , по которой пересекаются плоскости – границы полупространств , называ... Прямую , по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла. Грань двугранного угла Грань двугранного угла Грань двугранного угла Грань двугранного угла Грань двугранного угла Грань двугранного угла
Cлайд 4
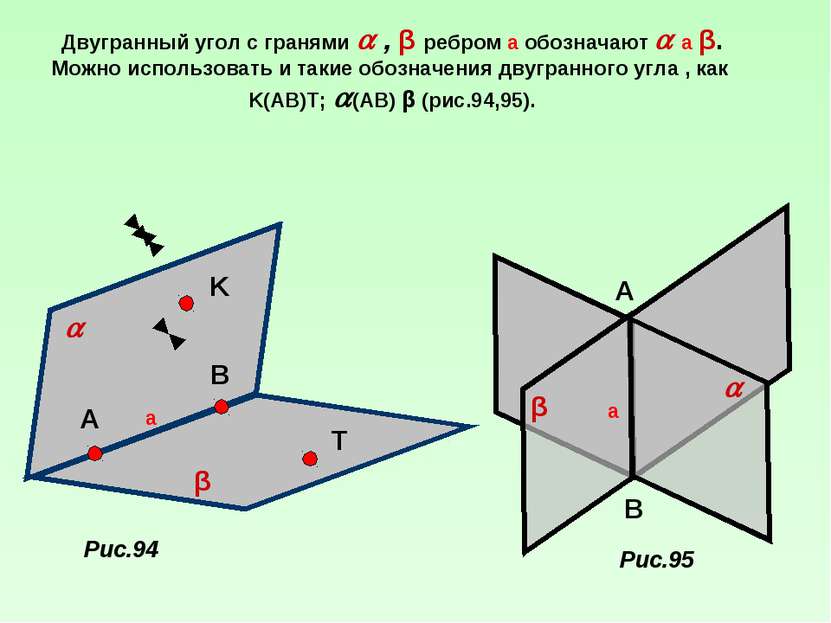
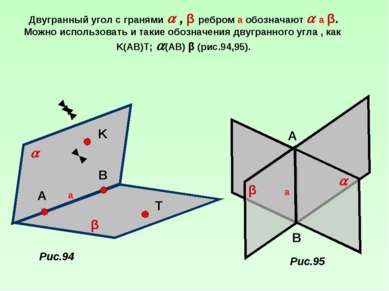Двугранный угол с гранями , β ребром а обозначают а β. Можно использовать и т... Двугранный угол с гранями , β ребром а обозначают а β. Можно использовать и такие обозначения двугранного угла , как K(AB)T; (AB) β (рис.94,95). Рис.94 Рис.95
Cлайд 5
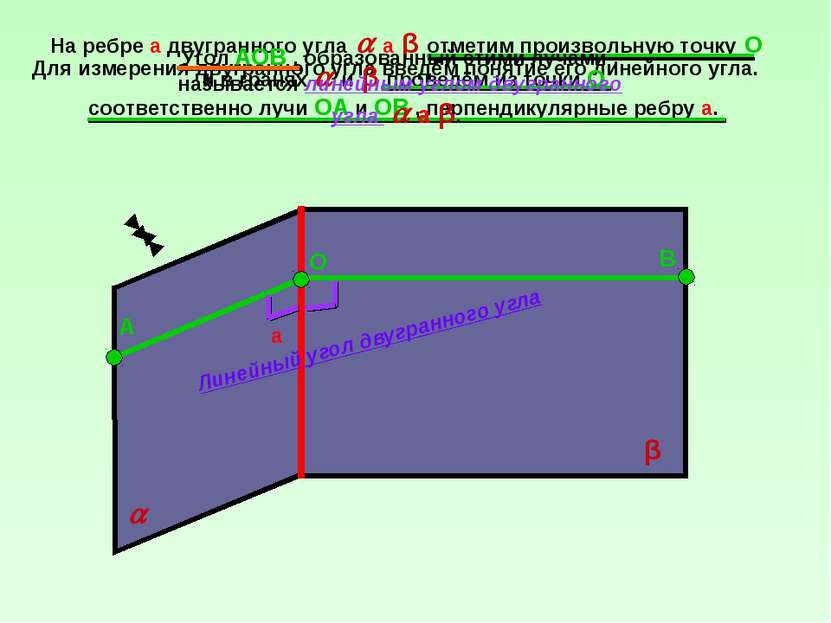
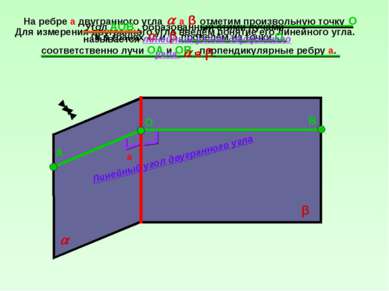Для измерения двугранного угла введём понятие его линейного угла. На ребре а ... Для измерения двугранного угла введём понятие его линейного угла. На ребре а двугранного угла а β отметим произвольную точку O и в гранях и β проведём из точки O соответственно лучи ОА и ОВ , перпендикулярные ребру а. а β О А В Угол АОВ , образованный этими лучами , называется линейным углом двугранного угла а β. Линейный угол двугранного угла
Cлайд 6
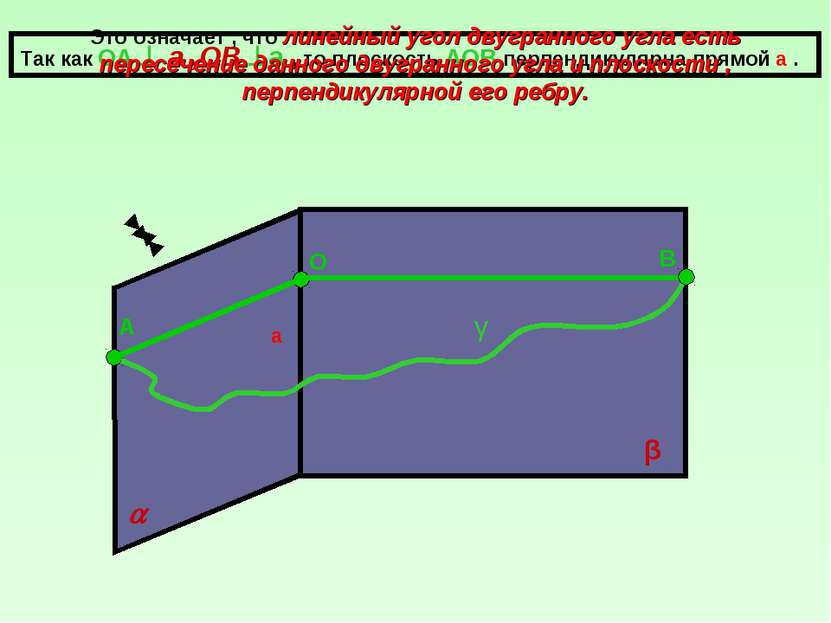
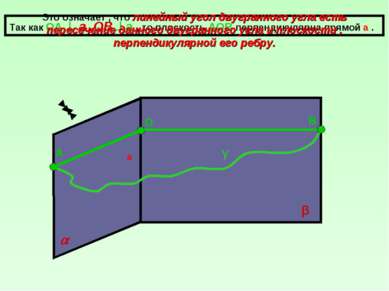а β О А В Так как ОА а ,ОВ а , то плоскость АОВ перпендикулярна прямой а . γ ... а β О А В Так как ОА а ,ОВ а , то плоскость АОВ перпендикулярна прямой а . γ Это означает , что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости , перпендикулярной его ребру.
Cлайд 7
Теорема : Величина линейного угла не зависит от выбора его вершины на ребре д... Теорема : Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. Определение : Величиной двугранного угла называется величина его линейного угла. Величина двугранного угла (измеренная в градусах ) принадлежит промежутку (0°;180°).
Cлайд 8
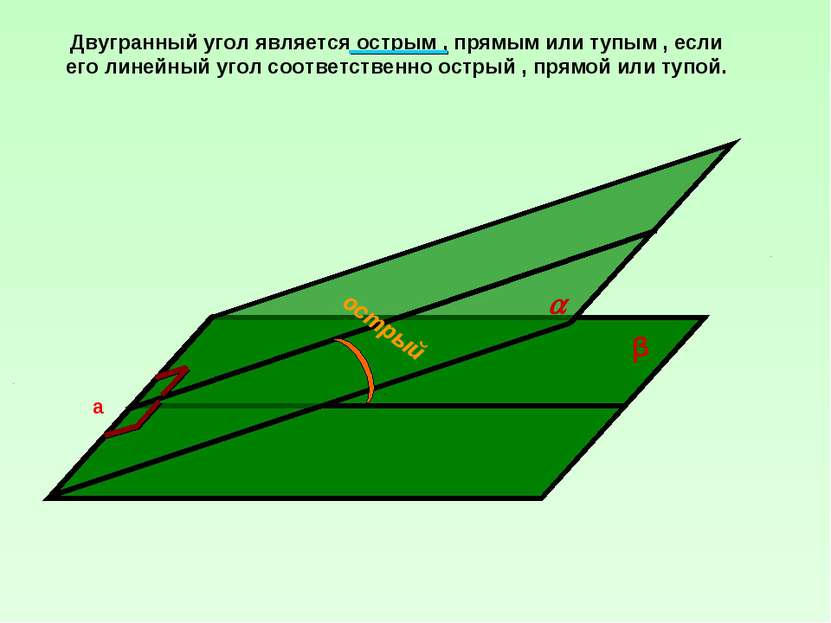
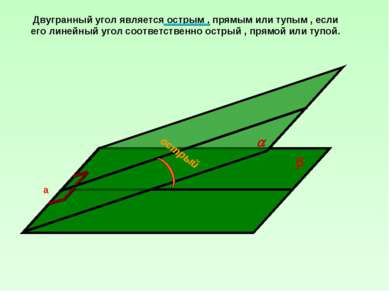Двугранный угол является острым , прямым или тупым , если его линейный угол с... Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый , прямой или тупой. острый
Cлайд 9
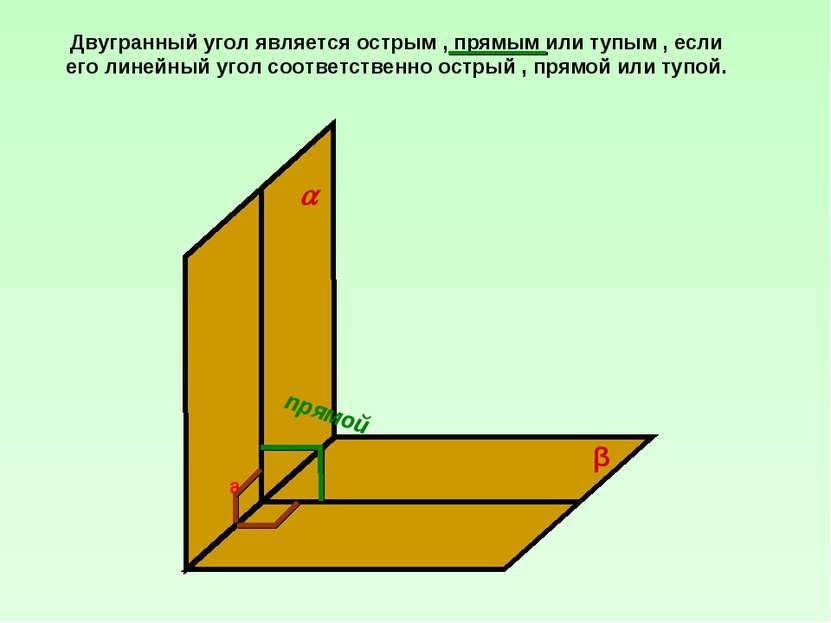
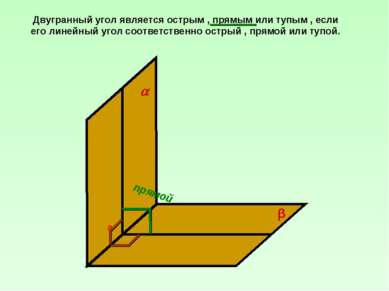Двугранный угол является острым , прямым или тупым , если его линейный угол с... Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый , прямой или тупой. прямой
Cлайд 10
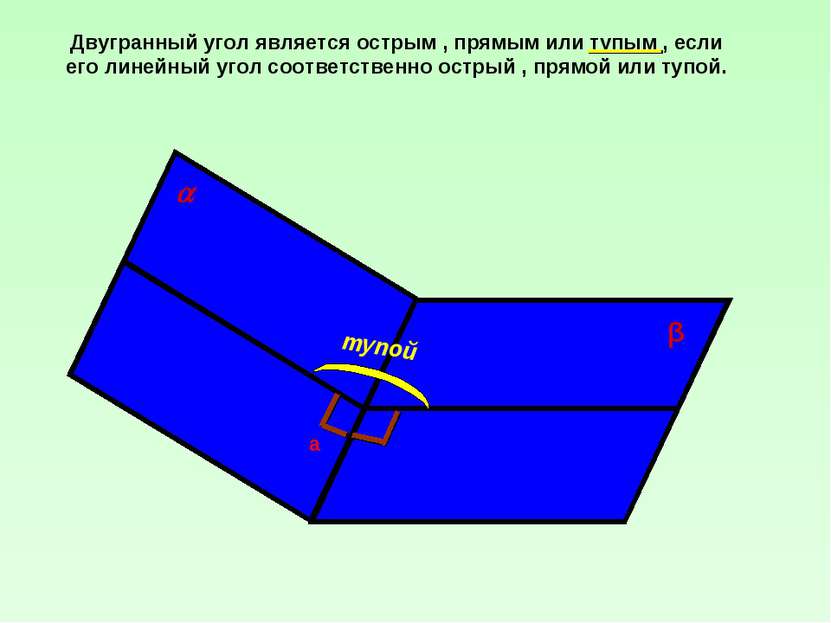
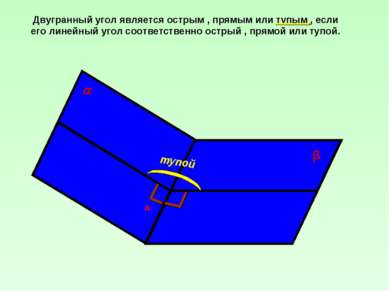Двугранный угол является острым , прямым или тупым , если его линейный угол с... Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый , прямой или тупой. тупой
Cлайд 11
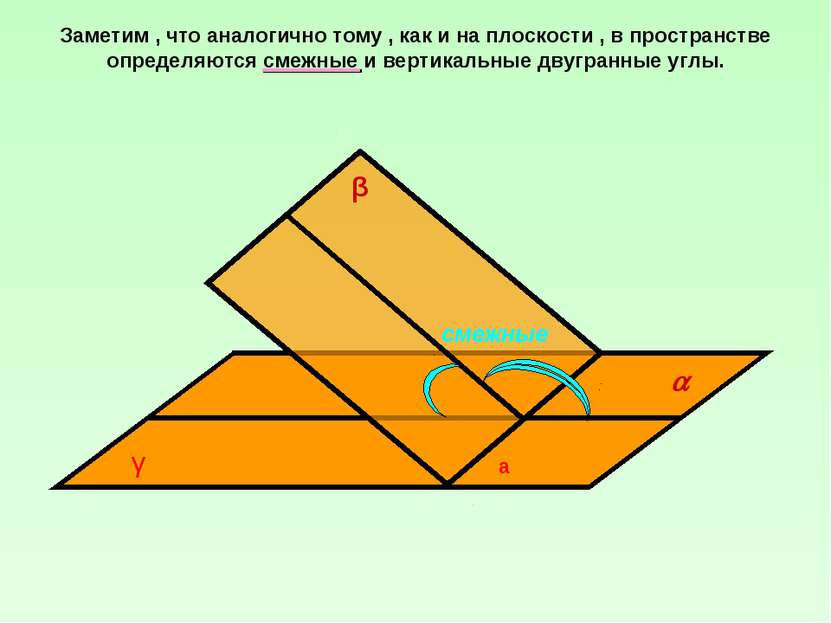
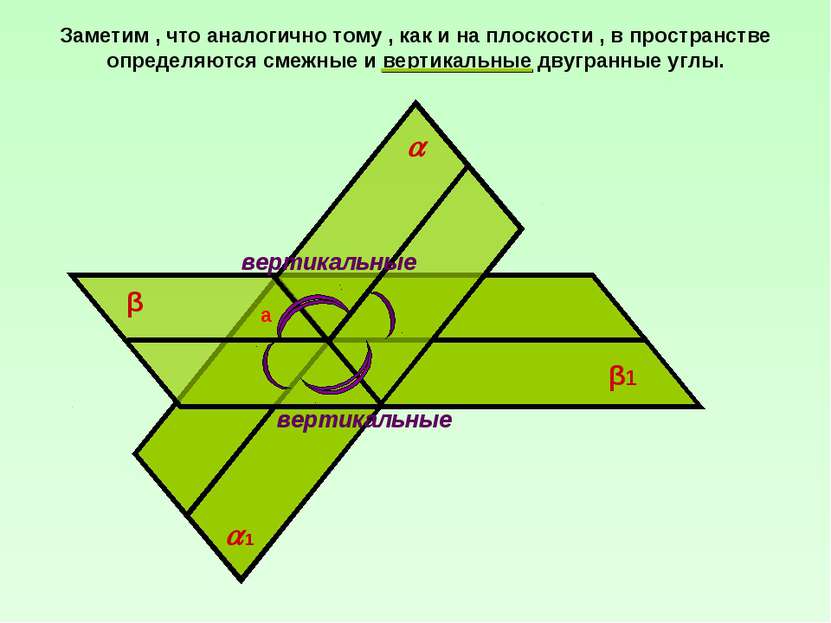
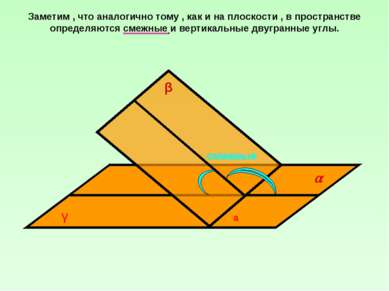Заметим , что аналогично тому , как и на плоскости , в пространстве определяю... Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.
Cлайд 12
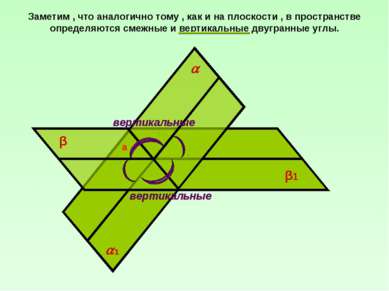Заметим , что аналогично тому , как и на плоскости , в пространстве определяю... Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы. β β1 а 1
Cлайд 13
Определение : Углом между двумя пересекающимися плоскостями называется наимен... Определение : Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов , образованных при их пересечении. Угол между параллельными или совпадающими плоскостями полагается равным нулю.
Cлайд 14
β β1 а 1 с Величина угла между плоскостями принадлежит промежутку [0°;90°]. β β1 а 1 с Величина угла между плоскостями принадлежит промежутку [0°;90°].
Cлайд 15
Учебник “ГЕОМЕТРИЯ 10 класс” Е.В.Потоскуев , Л.И. Звавич §14 Учебник “ГЕОМЕТРИЯ 10 класс” Е.В.Потоскуев , Л.И. Звавич §14

Презентации этого автора

Скачать эту презентацию

Похожие презентаци


Поделится
Наверх