X
Код презентации скопируйте его
Вписанные углы
Скачать эту презентацию
Презентация на тему Вписанные углы
Скачать эту презентациюCлайд 1
Cлайд 2
Cлайд 3
Cлайд 4
План урока: Повторение материала. Знакомство с определением вписанного угла. Доказательство теоремы, выражающей свойство вписанного угла. (3 случая) Формулировка двух следствий из теоремы. Практическая работа. Решение задач. Итог урока. Домашнее задание.
Cлайд 5
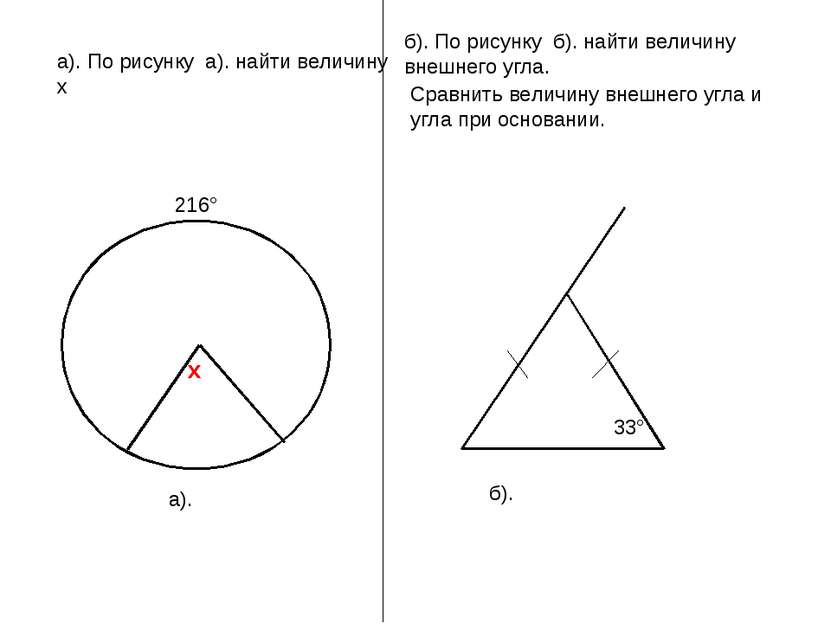
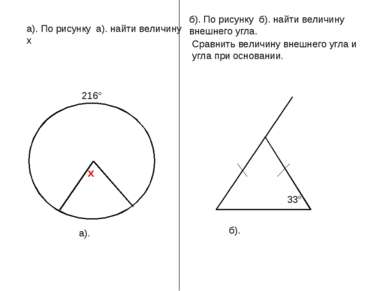а). б). По рисунку б). найти величину внешнего угла. Сравнить величину внешнего угла и угла при основании. б).
Cлайд 6
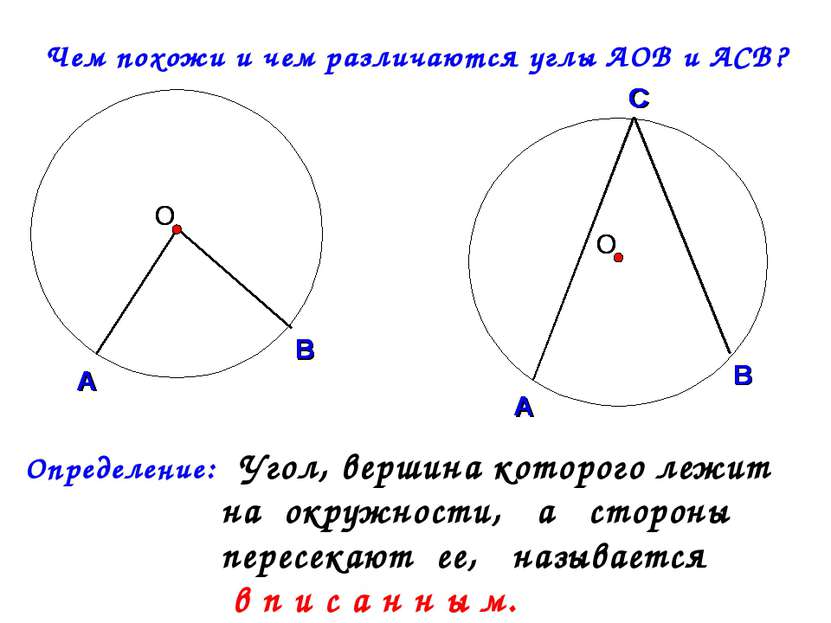
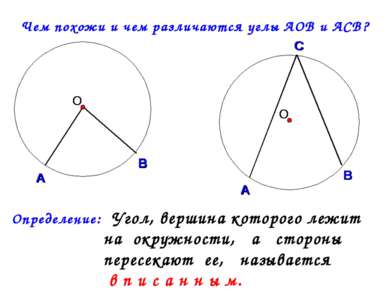Чем похожи и чем различаются углы АОВ и АСВ? Определение: Угол, вершина которого лежит на окружности, а стороны пересекают ее, называется в п и с а н н ы м.
Cлайд 7
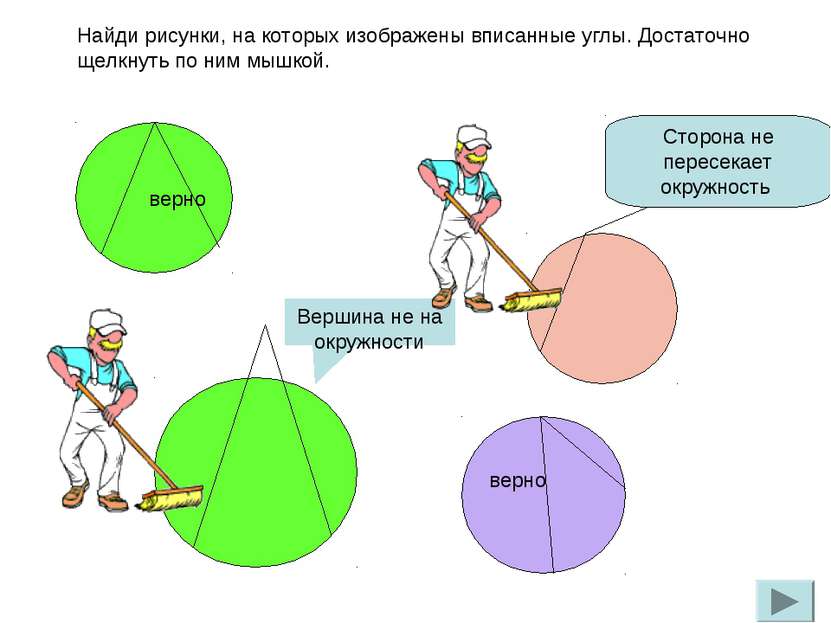
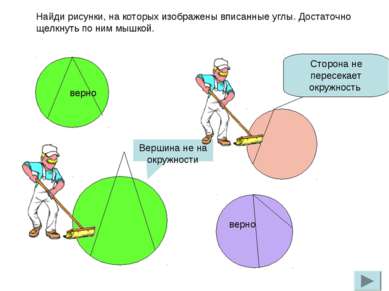Найди рисунки, на которых изображены вписанные углы. Достаточно щелкнуть по ним мышкой. верно верно Вершина не на окружности Сторона не пересекает окружность
Cлайд 8
Задание: Выразить величину вписанного угла,
Cлайд 9
А В С А В С D А В С Рассмотрим 3 случая:
Cлайд 10
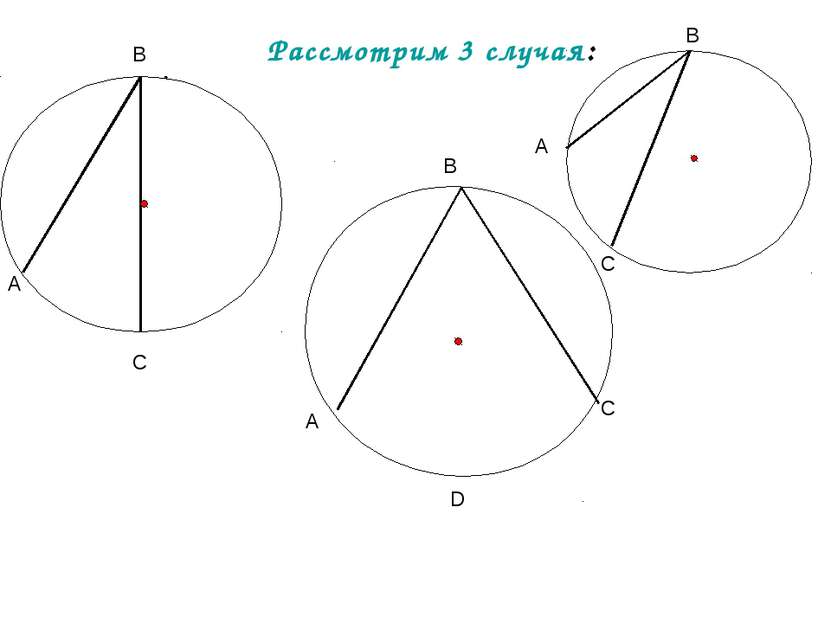
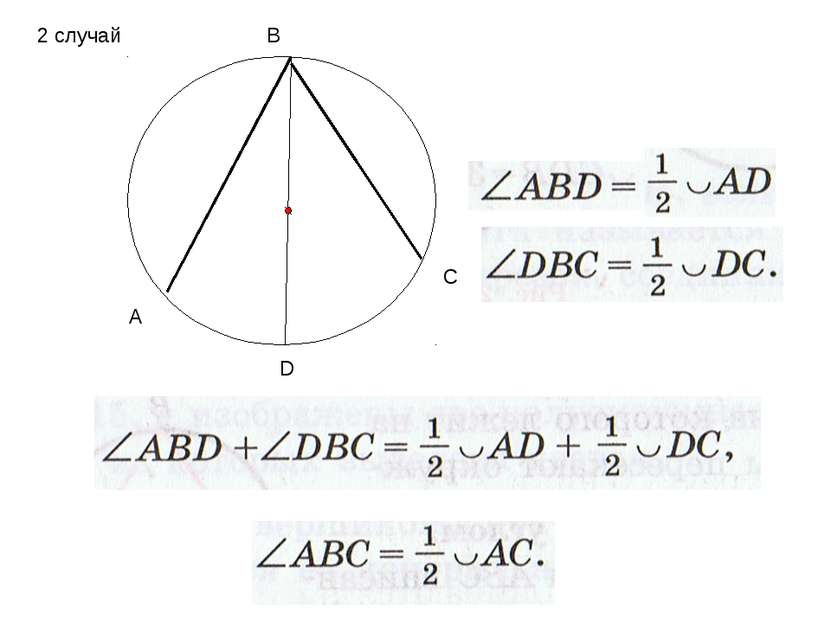
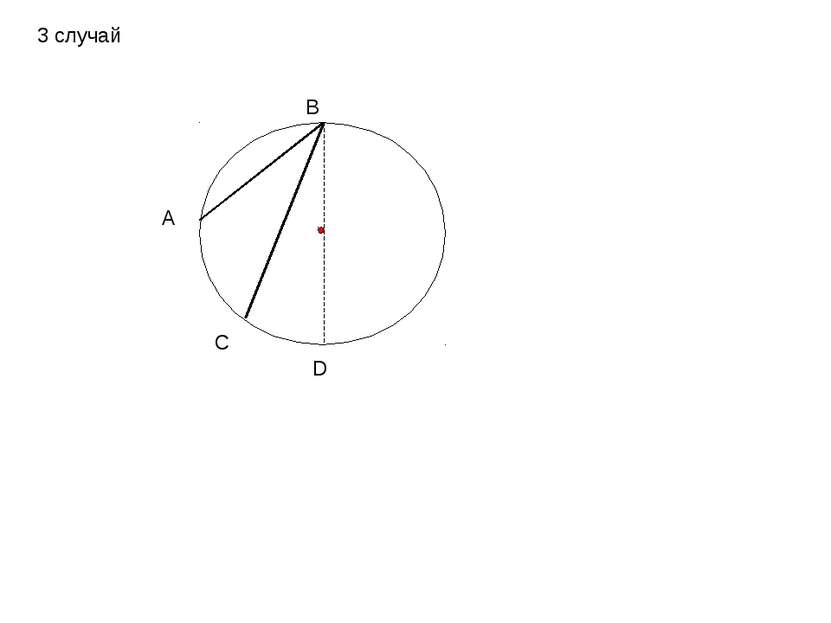
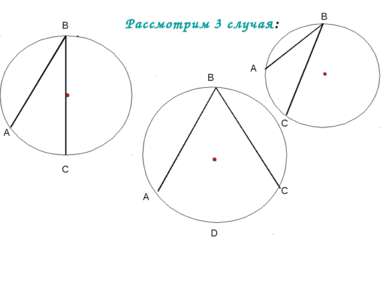
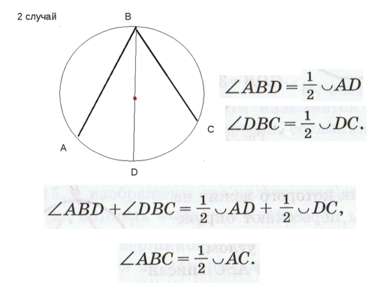
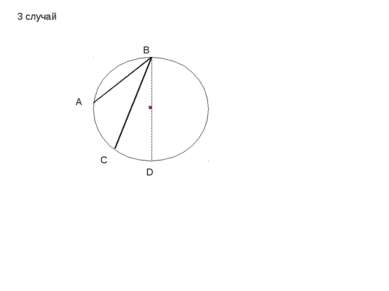
А В С О Теорема: Замечен факт: Вписанный угол измеряется половиной дуги, на которую он опирается. 1 случай
Cлайд 11
А В С О Дано: Док-ть: Доказательство: 1 2
Cлайд 12
А В С D 2 случай
Cлайд 13
А В С D 3 случай
Cлайд 14
Как быстро циркулем и линейкой построить сразу несколько углов равных данному ?
Cлайд 15
А В С Построение угла, равного данному. Дано: __А. Построить: __ О = __ А О D E
Cлайд 16
Cлайд 17
Следствие 1: Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Cлайд 18
Как быстро циркулем и линейкой построить прямой угол ?
Cлайд 19
В А Построение перпендикулярных прямых.
Cлайд 20
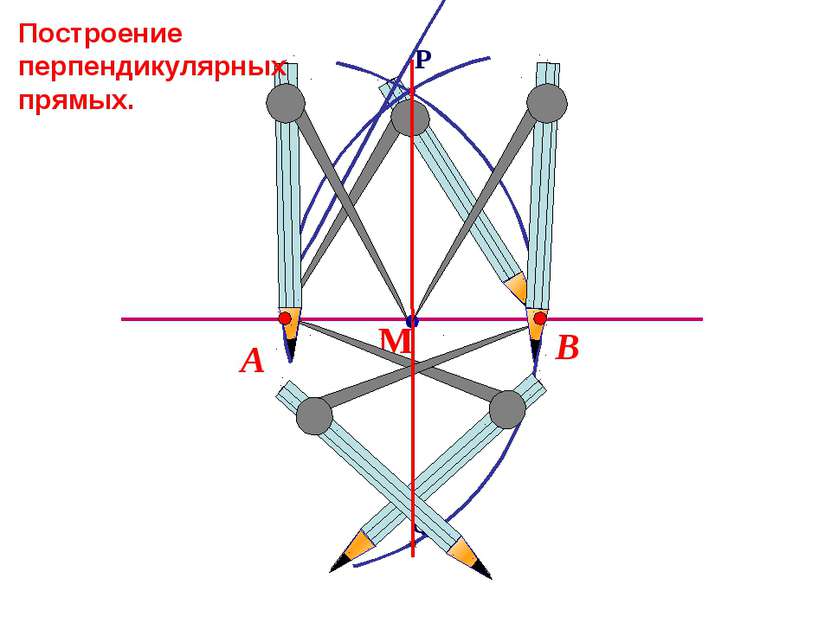
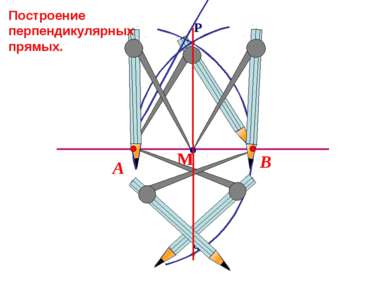
Как быстро циркулем и линейкой построить прямой угол ? Следствие 2: Вписанный угол, опирающийся на полуокружность - прямой.
Cлайд 21
Cлайд 22
Cлайд 23
Cлайд 24
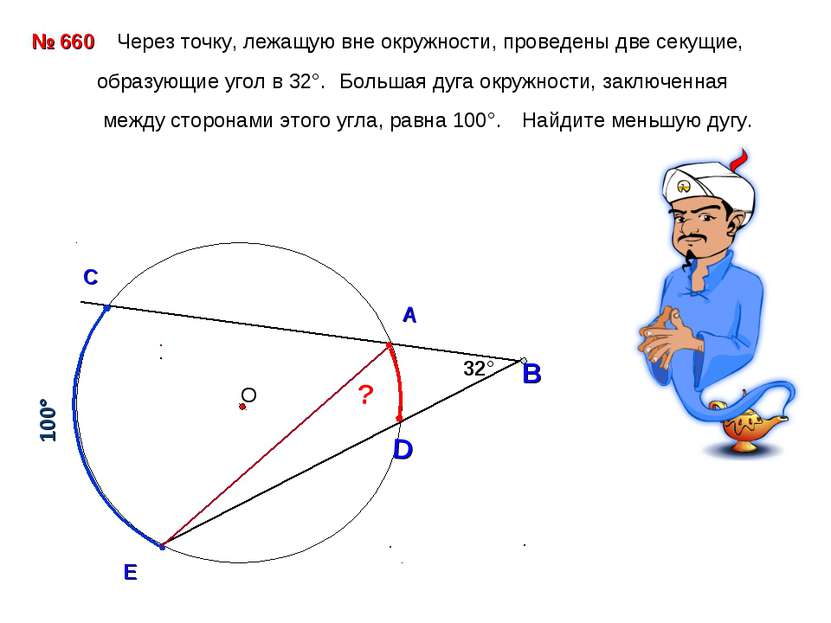
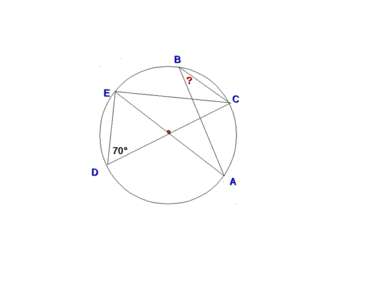
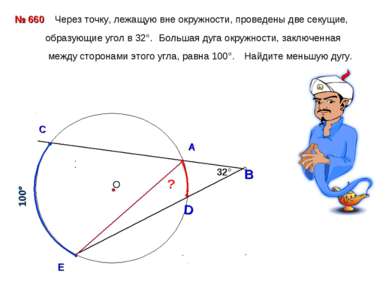В 32° 100° С E № 660 Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32°. Большая дуга окружности, заключенная между сторонами этого угла, равна 100°. Найдите меньшую дугу. О
Cлайд 25
Cлайд 26
30° Найдите градусную меру угла ABC. А D C B 60° 120°
Cлайд 27
Cлайд 28
А D Е С В ? 70°
Cлайд 29
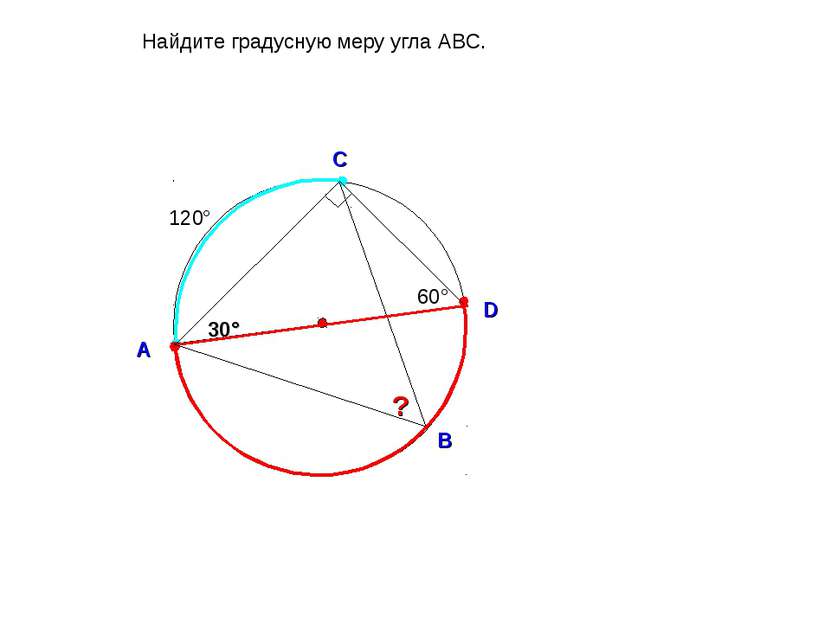
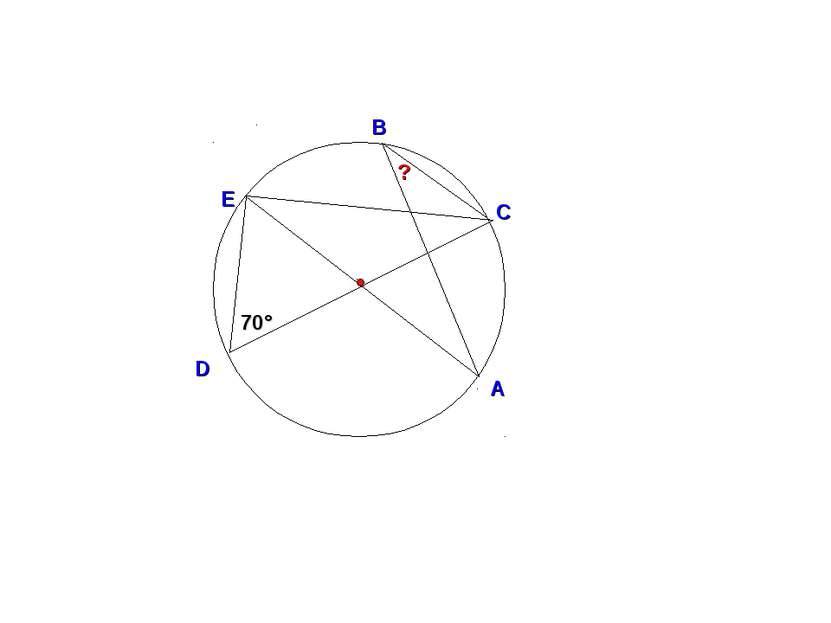
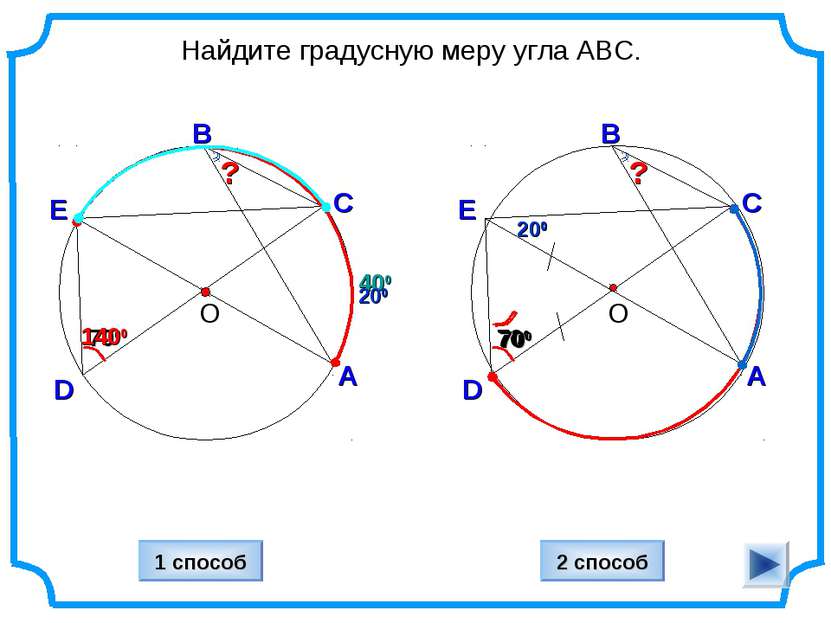
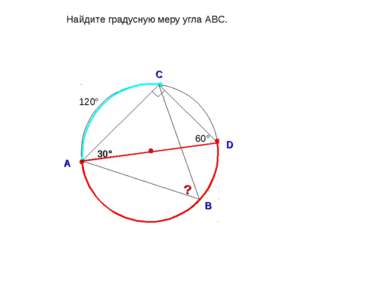
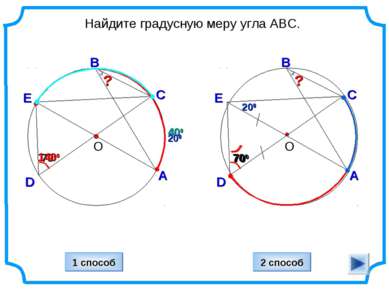400 D Найдите градусную меру угла ABC. О С А В 700 ? 200 1400 Е D О С А В 700 ? 200 Е 200 1 способ 2 способ
Cлайд 30
Cлайд 31
Итог урока: Найди ошибку в формулировках: 1. Вписанным называется угол, вершина которого лежит на окружности. Закончи фразу: 1. Вписанные углы равны, если… 2. Вписанный угол прямой, если… 2. Вписанный угол измеряется величиной дуги, на которую он опирается.
Cлайд 32
Домашнее задание: п.71, выучить определение вписанного угла, теорему о вписанном угле, (записав док-во 3 случая) и два следствия из нее, №657- выполнить письменно, №654-устно
Cлайд 33
Спасибо за внимание! Учитель математики МОУ «МСОШ № 16» города Миасса Челябинской области
