X
Код презентации скопируйте его
Магнитное поле в веществе
Скачать эту презентацию
Презентация на тему Магнитное поле в веществе
Скачать эту презентациюCлайд 1
Тема 3 Лекция 8 Магнитное поле в веществе 8.1 Источники магнитного поля вещества. Магнитные моменты элементарных частиц. Магнетон Бора и ядерный магнетон Источники магнитного поля в вещества суть орбитальное и спиновое движения связанных зарядов в составе атомов. Для орбитального магнитного момента электронов в атоме имеется естественная единица магнитного момента, называемая магнетон Бора , (8.1) где е - заряд электрона, - масса электрона, , – постоянная Планка. Для вещества в состоянии термодинамического равновесия суммарный магнитный момент всех атомов равен нулю. При включении внешнего магнитного поля орбитальное и спиновое движения атомных электронов изменяются. Эти измененные движения определяют молекулярные токи, индуцированные магнитным полем. Эти токи называются токами намагничивания или молекулярными токами. С их помощью описывается отклик вещества на внешнее магнитное поле, а именно создание дополнительного, индуцированного магнитного поля.
Cлайд 2
8.2 Действие магнитного поля на вещество. Индуцированные молекулярные токи. Вектор намагниченности Все вещества являются магнетиками, так как под действием внешнего поля они намагничиваются и их магнитный момент единицы объёма оказывается отличным от нуля. Он характеризует намагниченность вещества и называется вектор намагниченности , (8.2) где магнитный момент i - го атома, n - число атомов в единице объёма. На границе магнетика с вакуумом вектор намагниченности связан с возникающими поверхностными молекулярными токами соотношением , (8.3) где - линейная плотность поверхностных молекулярных токов, - вектор наружной нормали к поверхности магнетика.
Cлайд 3
8.3 Теорема о циркуляции вектора намагниченности Используя соотношение (8.3) можно показать, что намагниченность и токи намагничивания связаны между собой интегральным соотношением , (8.4) где слева стоит сила молекулярного тока через произвольную поверхность S внутри магнетика, определяемая объёмной плотностью молекулярных токов ( возникающих в неоднородном магнетике и пронизывающих эту поверхность), а справа стоит циркуляция вектора намагниченности вдоль замкнутой линии L, ограничивающей эту поверхность. С учетом как токов проводимости, создаваемых свободными зарядами в проводниках, так и токов намагничивания, создаваемых связанными зарядами в веществе, теорема о циркуляции векторного поля магнитной индукции вдоль произвольного замкнутого контура принимает вид , (8.5) где справа отделены токи проводимости от молекулярных токов.
Cлайд 4
8.4 Вектор напряжённости магнитного поля Используя выражение (8.4) можно переписать уравнение (8.5) в виде или . (8.6) Если теперь ввести вспомогательный вектор напряжённости магнитного поля , (8.7) то интегральное уравнение , (8.8) решается стандартными методами, если известны: правая часть этого уравнения (токи проводимости), поведение на границах магнетиков векторов магнитной индукции и напряжённости магнитного поля и связь вектора намагниченности с этими векторами магнитного поля.
Cлайд 5
8.5 Магнитная восприимчивость и магнитная проницаемость вещества Для получения полной системы уравнений необходимо задать так называемое материальное уравнение для вещества, связывающее намагниченность с напряженностью магнитного поля. Для изотропных сред в области относительно слабого магнитно поля справедливо соотношение , (8.9) выражающее линейную локальную связь. Здесь - безразмерная величина, называемая магнитной восприимчивостью. Теперь для вектора магнитной индукции можно написать , (8.10) где безразмерная величина называется относительной магнитной проницаемостью, а произведение - абсолютной магнитной проницаемостью.
Cлайд 6
Cлайд 7
8.6 Диамагнетики и парамагнетики На основе магнитных свойств почти все вещества отчётливо делятся на три большие группы: Диа -, Пара – и Ферромагнетики. У диамагнетиков < 0 и µ < 1. Атомы диамагнетиков при отсутствии внешнего магнитного поля не имеют постоянного магнитного момента. При включении внешнего магнитного поля в атомах любых магнетиков индуцируются токи, магнитные моменты которых направлены против внешнего магнитного поля (согласно правилу Ленца). Следовательно, диамагнетизм ослабляет внешнее магнитное поле. Идеальными диамагнетиками с = -1 и µ = 0 являются сверхпроводники, в которые внешнее магнитное поле вообще не проникает. В неоднородном магнитное поле диамагнетики выталкиваются из области сильного в область слабого поля. На этом эффекте основано подвешивание тел в магнитное поле, что используется для создания поездов на «магнитной подушке». К диамагнетикам относятся инертные газы, вода, золото, серебро, цинк, медь и некоторые другие материалы. Типичные значения магнитной восприимчивости у диамагнетиков -(10-6-10-5), то есть столь малы, что диамагнетизм перекрывается как парамагнитным, так и ферромагнитным эффектами.
Cлайд 8
У парамагнетиков > 0 и µ >1. При отсутствии внешнего магнитного поля атомы парамагнетика имеют постоянный магнитный момент. Во внешнем магнитном поле атомные магнитные моменты под действием вращающего момента сил стремятся принять ориентацию по полю. Полному выстраиванию всех атомных магнитных моментов в направлении поля препятствует тепловое движение атомов.
Cлайд 9
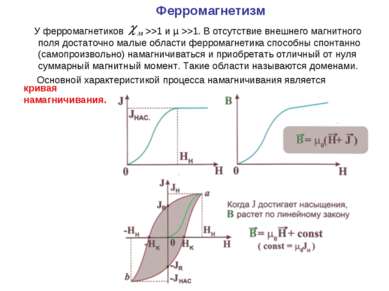Ферромагнетизм У ферромагнетиков >>1 и µ >>1. В отсутствие внешнего магнитного поля достаточно малые области ферромагнетика способны спонтанно (самопроизвольно) намагничиваться и приобретать отличный от нуля суммарный магнитный момент. Такие области называются доменами. Основной характеристикой процесса намагничивания является кривая намагничивания.
