X
Код презентации скопируйте его
Логарифмическая функция
Скачать эту презентацию
Презентация на тему Логарифмическая функция
Скачать эту презентациюCлайд 1
Cлайд 2
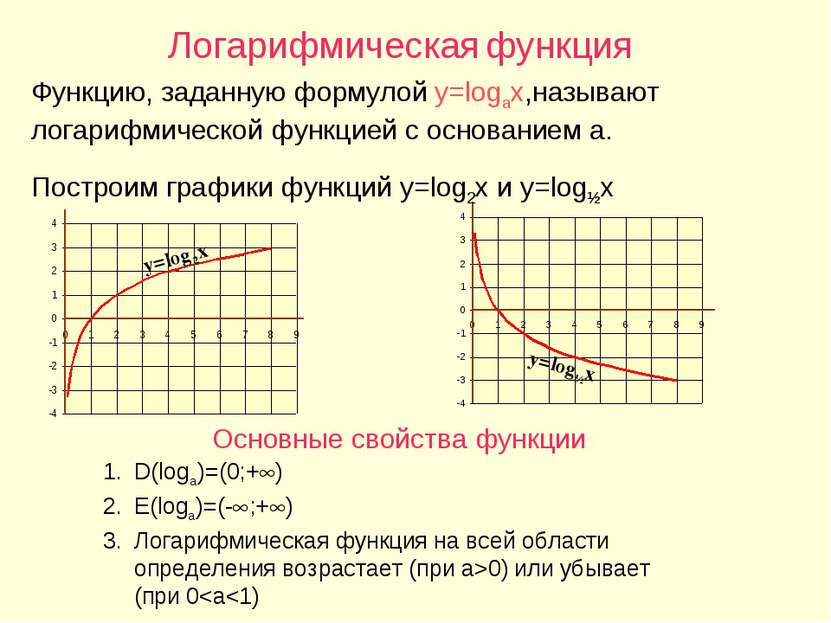
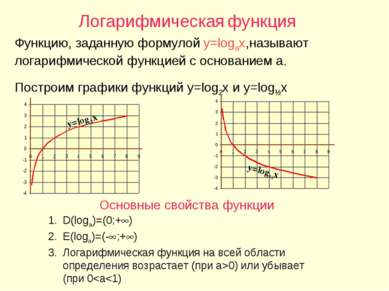Логарифмическая функция Функцию, заданную формулой y=logax,называют логарифмической функцией с основанием a. Построим графики функций y=log2x и y=log½x Основные свойства функции D(loga)=(0;+ ) E(loga)=(- ;+ ) Логарифмическая функция на всей области определения возрастает (при a>0) или убывает (при 0
Cлайд 3
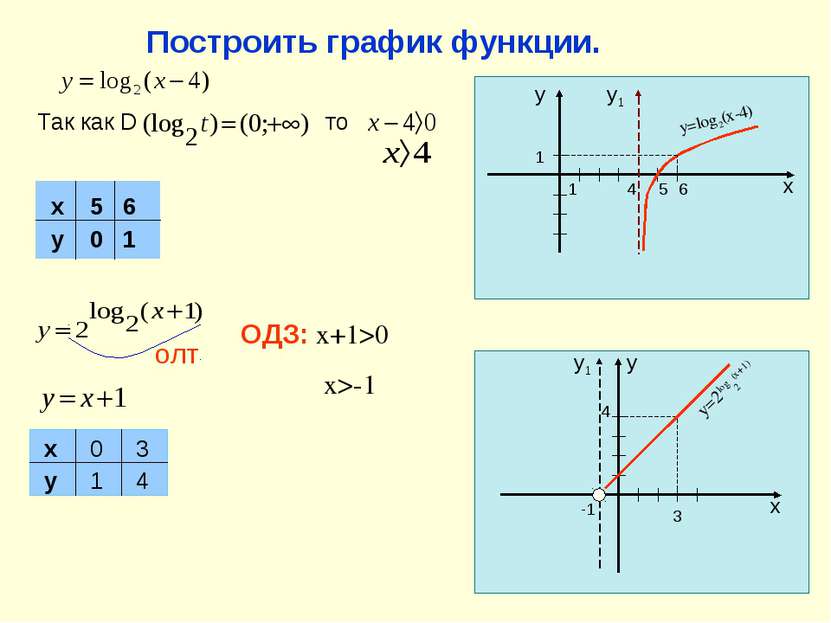
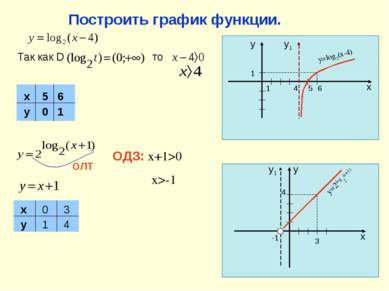
Рассмотрим примеры применения свойств логарифмической функции. Найдите область определения функции Т.к. D (log4t )=(0;+ ), то получаем Решая это неравенство методом интервалов имеем: Ответ: D (log4t )=(- ;-3) (2;+ ) 2. Сравнить числа: и Основание логарифмической функции больше 1, значит она возрастает на всей числовой прямой. Так как 3,8
Cлайд 4
Построить график функции. Так как D олт ОДЗ: x+1>0 x>-1 то
Cлайд 5
При решении всех логарифмических уравнений необходимо помнить, что D (logat)=(0;+ ) Поэтому полученные корни обязательно проверяют либо подстановкой в условие уравнения, либо предварительно надо найти ОДЗ и проверить принадлежность корней этой области.
Cлайд 6
1 способ: Использование определения логарифма log a x=b, ab=x Например. log3(2-x)=2 2-x=32 2-x=9 x=-7 ОДЗ: 2-x>0 x
Cлайд 7
2 способ: Использование непрерывности функции log5(x+4)=log5(5x-3) Логарифмы равны, основания равны, значит равны выражения под знаком логарифма. x+4=5x-3 -4x=-7 x=1¾ ОДЗ: x+4>0 5x-3>0 x>-4 x>0,6 -4 0,6 x (0,6;+ ) 1¾ ОДЗ Ответ: 1¾
Cлайд 8
3 способ: Использование основных свойств логарифма. lgx-lg5=lg12 lgx=lg12+lg5 lgx=lg60 x=60 Ответ: 60 ОДЗ: x>0 x (0;+ ) 60 ОДЗ
Cлайд 9
4 способ: Переход к квадратному уравнению. log23x-2log3x-3=0 Пусть log3x=y y2-2y-3=0 y1=3; y2=-1 Тогда log3x=3 log3x=-1 x=33 x=3-1 x=27 x=1⁄3 ОДЗ: x>0 x (0;+ ) 27 ОДЗ, 1⁄3 ОДЗ Ответ: 1⁄3; 27
Cлайд 10
Основные свойства логарифмов
