X
Код презентации скопируйте его
Четырёхугольники. Решение задач
Скачать эту презентацию
Презентация на тему Четырёхугольники. Решение задач
Скачать эту презентациюCлайд 1
Четырехугольники 9 класс Учитель математики Щедрина Р.Н. ОГОУ «Орловская общеобразовательная школа – интернат V вида» 2010г
Cлайд 2
Цели урока Систематизировать и обобщить знания учащихся. Проверить уровень усвоения темы. Формировать умения применять знания к решению задач. Привить интерес к предмету.
Cлайд 3
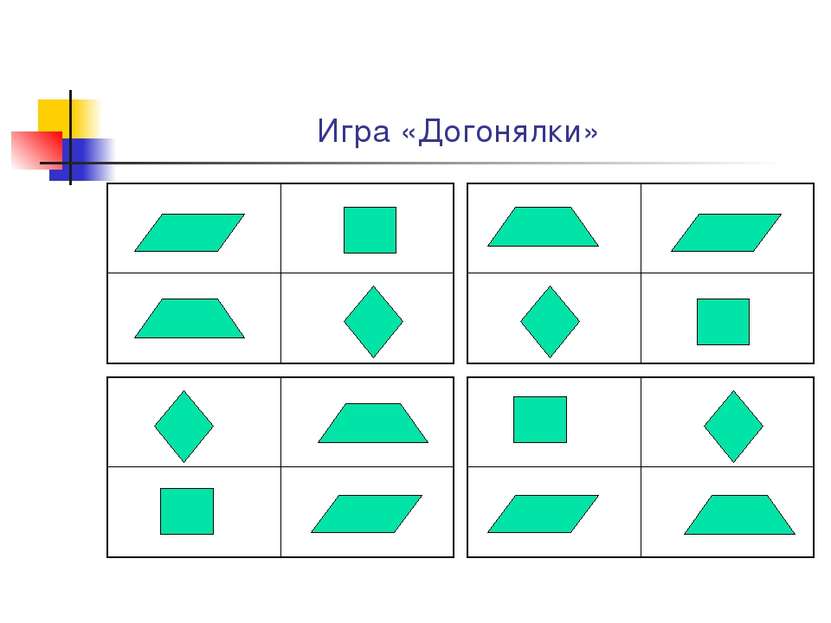
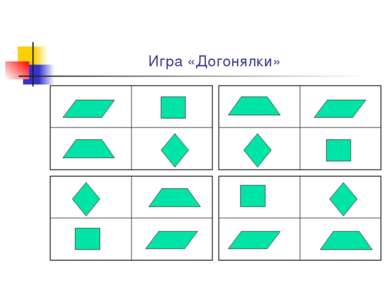
Ход урока Организационный момент. Математический диктант. Решение задач. Игра «Догонялки» Задание на дом. Самостоятельная работа. Подведение итогов.
Cлайд 4
Организационный момент 1.Мы закончили изучение темы: «Четырехугольники». Сегодня еще раз вспомним определения и свойства известных вам фигур. И расскажу я вам сказку. Сказки бывают волшебные, а наша еще и полезная. Почему, потом поймете. Вы будете помогать мне. Как называется сказка, вы должны угадать. Жил был вот такой четырехугольник Звали его Параллелограмм. Давайте вспомним определение и свойства Параллелограмма. 2.Ходил Параллелограмм по свету, и стало тяготить его одиночество: ни побеседовать задушевно не с кем, ни потрудиться в хорошей дружной компании. А уж, какое веселье одному? Весело бывает только с друзьями, и решил Параллелограмм поискать родственников. - Ежели встречу родственника, то я сразу узнаю его, - думал Параллелограмм, - ведь он на меня должен быть чем-то похож. Однажды встречает он на пути такую фигуру
Cлайд 5
Стал Параллелограмм к ней приглядываться, что-то знакомое, родное увидел он в этой фигуре, и спросил он тогда: - Как тебя зовут, приятель? - Называют меня Прямоугольником. Давайте вспомним определение и свойства Прямоугольника. Обрадовались фигуры, что нашли друг друга. Стали теперь они вдвоем жить-поживать, вместе трудиться, вместе веселиться и по белу свету шагать. Вот отдыхают они на опушке леса и видят: выходит из-за кустарника какие-то фигуры и направляются прямо к ним. А вид они имели такой: -Кто же вы? -Да мы же родственники! - воскликнул Параллелограмм. Как же мы теперь озаглавим эту сказку? А теперь Параллелограмм, Прямоугольник, Ромб, Квадрат загадают вам загадки. Постарайтесь их отгадать.
Cлайд 6
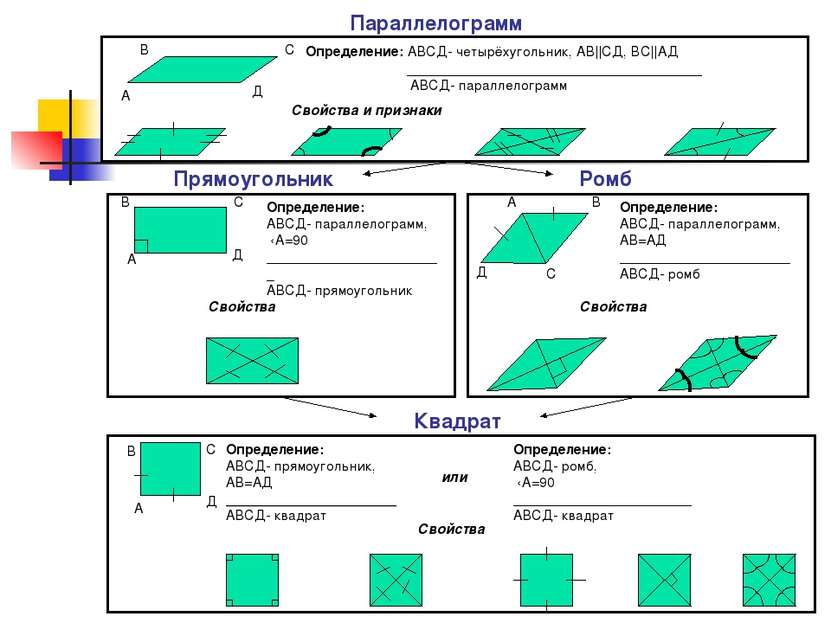
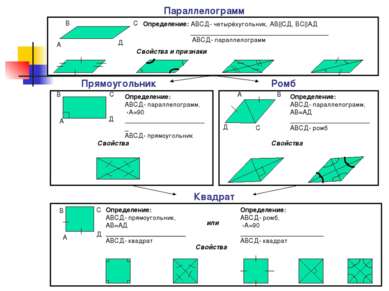Квадрат Параллелограмм Прямоугольник Ромб А В С Д Определение: АВСД- четырёхугольник, АВ||CД, ВС||АД ______________________________________ АВСД- параллелограмм Определение: АВСД- параллелограмм, ‹А=90 _______________________ АВСД- прямоугольник Свойства и признаки А В С Д Свойства Определение: АВСД- параллелограмм, АВ=АД ______________________ АВСД- ромб А В С Д Свойства Определение: АВСД- прямоугольник, АВ=АД ______________________ АВСД- квадрат или Определение: АВСД- ромб, ‹А=90 _______________________ АВСД- квадрат Свойства А В С Д
Cлайд 7
Математический диктант 1.Верно ли, что каждый параллелограмм является ромбом? 2.Является ли прямоугольником параллелограмм, у которого есть прямой угол? 3.Если две стороны четырёхугольника параллельны, а две другие нет, то он является трапецией? 4.Диагонали квадрата являются биссектрисами его углов? 5.У ромба и параллелограмма диагонали перпендикулярны? 6.Диагонали параллелограмма 5см и 5см. Является ли этот параллелограмм прямоугольником? Ответ: 1.нет 2.да 3.да 4.да 5.нет 6.да
Cлайд 8
Загадка Параллелограмма A B C D 30 160 Найди ошибку! Решение Т.К АВСD- параллелограмм (по условию), то ВС || АD(по определению), ‹ А и ‹ В – внутренние односторонние углы при параллельных прямых ВС и АD, секущей АВ (по определению), ‹ А + ‹ В = 180 (по свойству) 150
Cлайд 9
Загадка Прямоугольника ‹1 = 50 Найти: ‹2, ‹3. Подсказка LN ? KM ? LO ? KO ? ∆ LOK ? ‹2 ? ‹3 ? ‹1 + ‹2 + ‹3 = ? ‹2 + ‹3 = ? K L M N 1 3 2 О Решение Т.к. LMNK – прямоугольник (по условию), LN = KM, LN ∩ KM = О, KO = OM = LO = KO (по свойству), ∆ LOK–равнобедренный с основанием KL(по определению), то ‹2 = ‹3 (по свойству) ‹1 + ‹2 + ‹3 = 180 (по свойству), ‹2 + ‹3 = 130 , ‹2 = ‹3 = 65 65 65
Cлайд 10
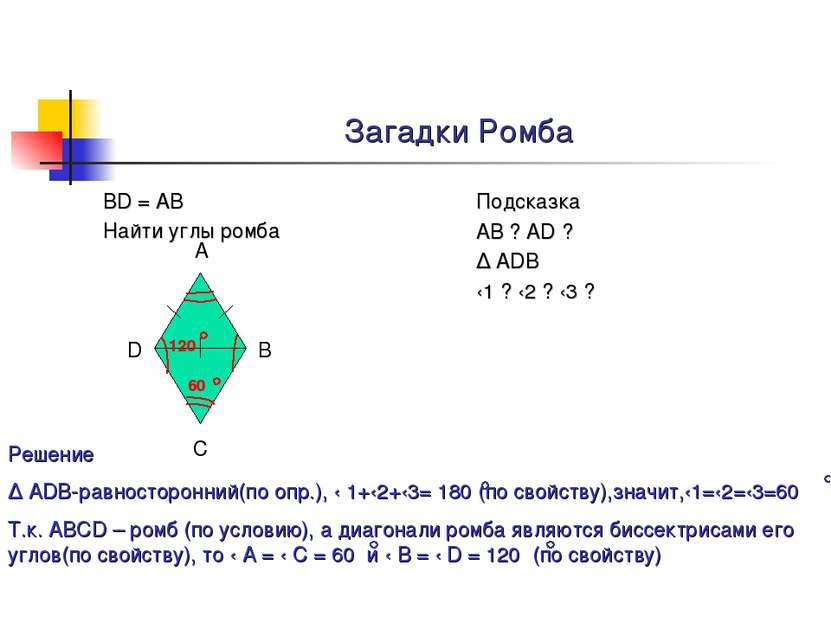
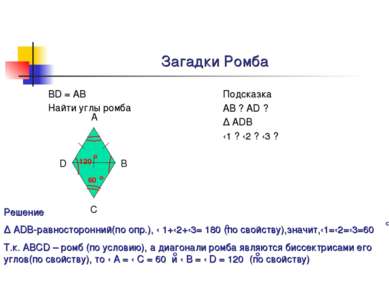Загадки Ромба BD = AB Найти углы ромба Подсказка AB ? AD ? ∆ ADВ ‹1 ? ‹2 ? ‹3 ? Решение ∆ ADB-равносторонний(по опр.), ‹ 1+‹2+‹3= 180 (по свойству),значит,‹1=‹2=‹3=60 Т.к. АВСD – ромб (по условию), а диагонали ромба являются биссектрисами его углов(по свойству), то ‹ А = ‹ С = 60 и ‹ В = ‹ D = 120 (по свойству) А D В С 60 120
Cлайд 11
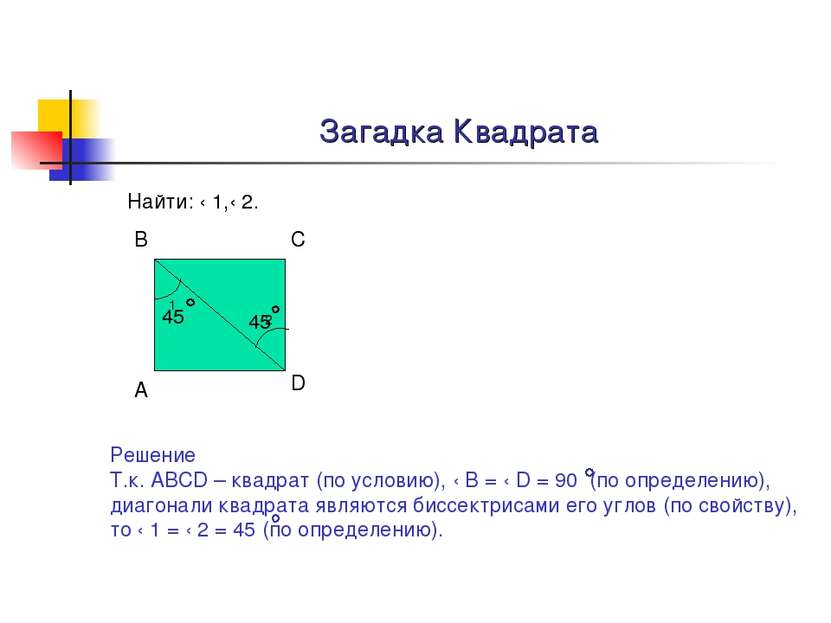
Загадка Квадрата Найти: ‹ 1,‹ 2. 1 2 А В С D Решение Т.к. АВСD – квадрат (по условию), ‹ В = ‹ D = 90 (по определению), диагонали квадрата являются биссектрисами его углов (по свойству), то ‹ 1 = ‹ 2 = 45 (по определению). 45 45
Cлайд 12
Молодцы, ребята, справились с задачами! - О каком четырёхугольнике в сказке не упоминалось? Почему?
Cлайд 13
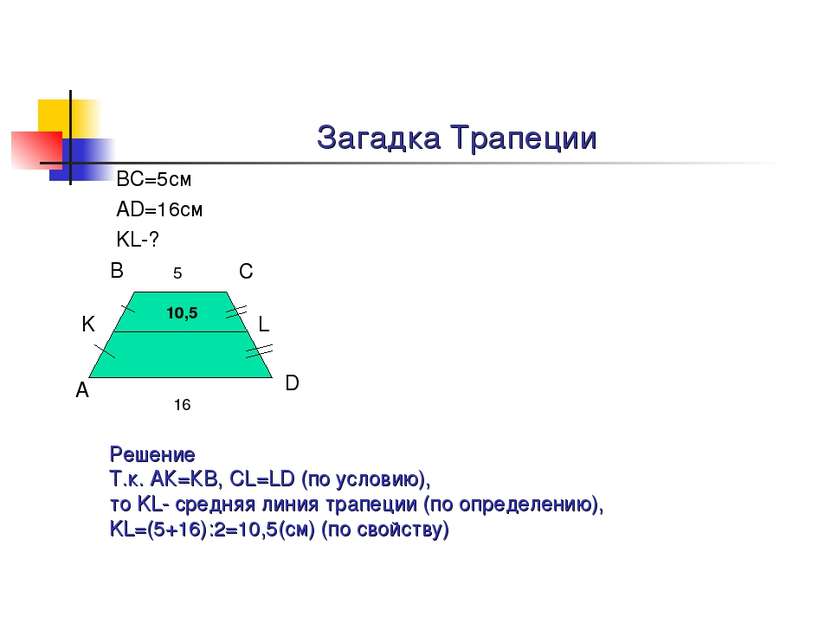
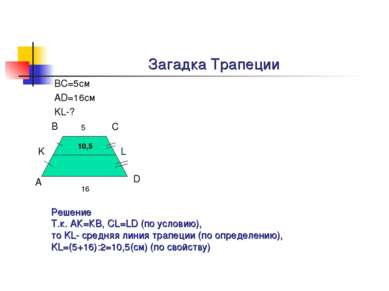ВС=5см АD=16см KL-? А В С D K L 5 16 Решение Т.к. АК=КВ, CL=LD (по условию), то KL- средняя линия трапеции (по определению), KL=(5+16):2=10,5(см) (по свойству) 10,5 Загадка Трапеции
Cлайд 14
Игра «Догонялки»
Cлайд 15
Самостоятельная работа 1.Чем отличаются свойства диагоналей прямоугольника от ромба? Прямоугольник Ромб 1)… 1) - 2)- 2)… 3)- 3)… 2.Сумма двух углов параллелограмма 120 . Найти углы параллелограмма. А В С равны перпендикулярны ‹ А = ‹ С = 60 (по свойству) ‹ А + ‹ С = 120 (по условию) ‹ В = ‹ D = 120 (по свойству) D Решение
Cлайд 16
Спасибо за урок!
Cлайд 17
Литература Газета «Математика».- Изд.: Первое сентября, 2000-2007.
