X
Код презентации скопируйте его
Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители
Скачать эту презентацию
Презентация на тему Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители
Скачать эту презентациюCлайд 1
КВАДРАТНЫЙ ТРЕХЧЛЕН
Cлайд 2
КВАДРАТИЧНАЯ ФУНКЦИЯ
Cлайд 3
Алгоритм решения квадратного уравнения ПО ФОРМУЛЕ КОРНЕЙ: Найти число, называемое дискриминантом квадратного уравнения и равное D = b²- 4ac. 2) Дискриминант показывает сколько корней имеет уравнение - если D
Cлайд 4
Разложение квадратного трехчлена на множители
Cлайд 5
Определение Многочлен ax²+bx+c , где а, в, с – числа (коэффициенты), причем а ≠ 0 называется квадратным трехчленом Причем: а – старший коэффициент, в - второй коэффициент с – свободный член
Cлайд 6
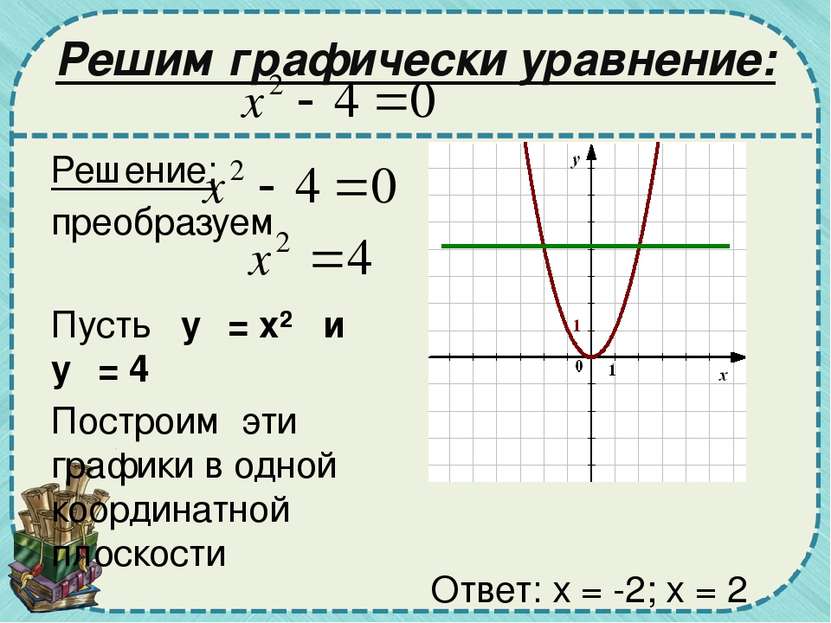
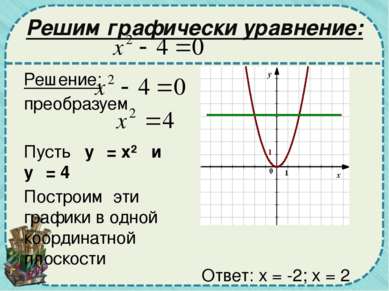
Решим графически уравнение: Решение: преобразуем Пусть у₁ = х² и у₂ = 4 Построим эти графики в одной координатной плоскости Ответ: х = -2; х = 2
Cлайд 7
Введение новой переменной Умение удачно ввести новую переменную – облегчает решение Например: надо решить уравнение (2х+3)² = 3(2х+3) – 2. Решение: пусть: а = 2х + 3. Произведем замену переменной: а² = 3а - 2. Тогда получим уравнение а² - 3а + 2 = 0 и у него D > 0. Решим квадратное уравнение и получим: а₁ = 1, а₂ = 2. Произведем обратную замену и вернемся к переменной х: 1). если а₁ = 1, то 2х + 3 = 1 и тогда х₁ = - 1; 2). если а₂ = 2, то 2х + 3 = 2 и тогда х₂ = - 0,5 Ответ: -1; -0,5.
Cлайд 8
Запомним Функция у = ax²+bx+c, где а, в, с – произвольные числа, причем а ≠0 называется квадратичной. Графиком квадратичной функции является парабола
Cлайд 9
Ветви параболы у = ax²+bx+c направлены вверх, если а > 0, и вниз если а < 0 Как найти координаты вершины параболы? – абсцисса х₀ вершины параболы вычисляется по формуле х₀ = - в/2а - ордината у₀ вершины параболы вычисляется подстановкой найденной х₀ в заданную функцию Осью симметрии параболы является прямая х = - в/2а Запомним
Cлайд 10
Найти координаты вершины параболы, её ось симметрии и построить её: у = 2х² - 8х + 1 у = - 2х² +16х – 5 Т.к. а =2 ; в =-8; с =1 то х₀ = 8 : (2·2)=2 у₀= 2·2² - 8·2 + 1=-7 Значит: (2; -7) координаты вершины, а ось симметрии параболы: х=2 2) Т.к. а=-2; в=16; с=-5 то х₀ = -16 : (2·(-2)) = 4 у₀ = -2· 4² + 16·4 - 5 = 27 Значит: (4; 27) координаты вершины; ось симметрии: х=4
Cлайд 11
Самостоятельно: вычислить координаты вершины параболы 1) у = х² + 4х + 5 2) у = 2х² + 4х 3) у = -3х² + 6х + 1 4) у = 3х² - 12х 5) у = х² + 6х - 2 6) у = -2х² + 8х - 5 7) у = -4х² - 8х Проверим: 1) (-2; 1) 2) (-1; -2) 3) (1; 4) 4) (2; - 12) 5) (-3; - 11) 6) (2; 3) 7) (-1; 4)
Cлайд 12
Рефлексия: 1) Сегодня на уроке я запомнил… 2) Сегодня на уроке я научился… 3) Сегодня на уроке я узнал … 4) Сегодня на уроке я выучил… 5) Сегодня на уроке было интересно … 6) Сегодня на уроке мне понравилось …
Cлайд 13
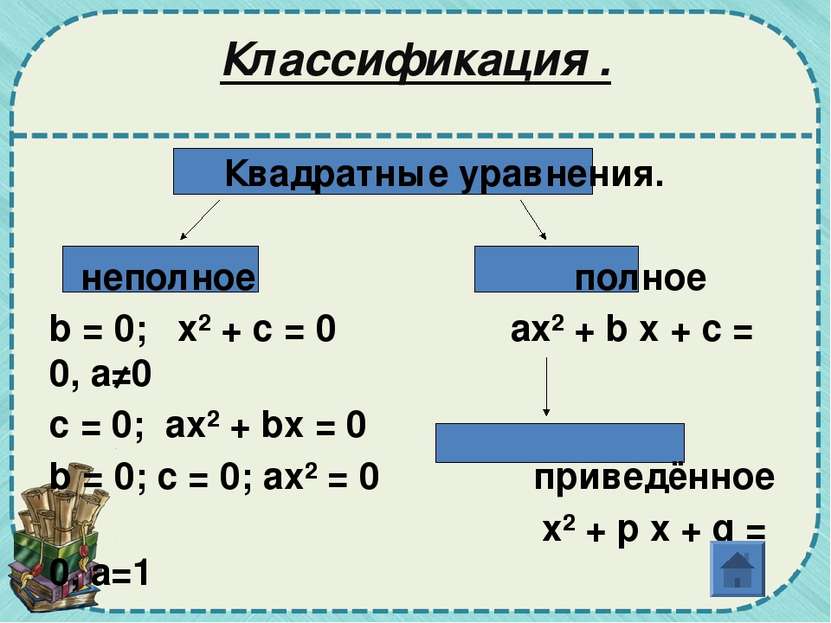
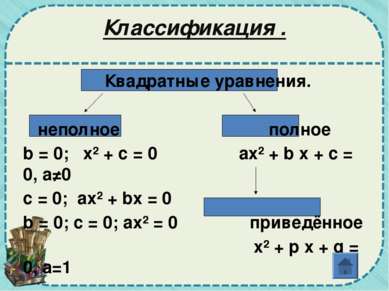
Содержание: Определение квадратного уравнения Классификация квадратных уравнений Способы решения квадратного уравнения
Cлайд 14
Запомним Решить квадратное уравнение – это значит найти все его корни или установить, что их нет. Причем: квадратное уравнение может иметь либо 2 корня (если D >0), либо 1 корень (если D = 0), либо вообще не иметь корней (если D
Cлайд 15
Рассмотрим ещё одно решение: Решим уравнение: х² + 6х - 7 = 0. Решение: х² + 6х -7 = 0. х² + 2 · 3 · х + 9 – 9 – 7 = 0 (х² + 6х + 9) - 9 – 7 = 0 (х +3)² – 16 = 0. (х +3)² = 16. Значит: х +3 = 4 и х + 3 = -4. х = 1 х =-7. Ответ: 1; -7.
Cлайд 16
- если D=0, то данное квадратное уравнение имеет единственный корень, который равен - если D>0, то данное квадратное уравнение имеет два корня, которые равны
Cлайд 17
Решить уравнение: 2x2- 5x + 2 = 0 Здесь a = 2, b = -5, c = 2. Имеем D = b2- 4ac = (-5)2- 4 2 2 = 9. Так как D > 0, то уравнение имеет два корня. Найдем их по формуле то есть x₁ = 2 и x₂ = 0,5 - корни заданного уравнения.
Cлайд 18
Решить самостоятельно: x2- 2x + 1 = 0. 2x2- 3x +5= 0. Проверим 1 уравнение: получили один корень х = 1, т.к. D = 0 Проверим 2 уравнение: уравнение не имеет действительных корней, т.к. D < 0
Cлайд 19
Работаем в парах: 1) Выберите квадратные уравнения и определите значения их коэффициентов: А) 2х² – 8 = 0; Б) -х² + 4х + 1 = 0; В) 3х³ + 2х – 9 = 0; Г) 5х – 3х² +2 = 0; Д) х – 3 = 0; Е) 3 – 5х² – х = 0; Ж) х² – х = 0. И) х² + 5 - 2х = 0 2) По коэффициентам указать приведенные уравнения. 3) Из квадратных уравнений выбрать неполные и решить их.
Cлайд 20
Проверим: Квадратные уравнения: А) 2х² – 8 = 0, где а=2; в=0; с=-8 Б) -х² + 4х + 1 = 0, где а=-1; в=4; с=1 Г) 5х – 3х² + 2 = 0, где а=-3; в=5; с=2 Е) 3 – 5х² – х = 0, где а=-5; в=-1; с=3 Ж) х² – х = 0, где а=1; в=-1; с=0 И) х² + 5 - 2х = 0, где а=1; в=-2; с=5
Cлайд 21
Проверим: 2) Приведенные квадратные уравнения: И) х² + 5 - 2х = 0 3) Неполные квадратные уравнения: А) 2х² – 8 = 0 и Ж) х² – х = 0 Решения: 2х² – 8 = 0 и х² – х = 0 2(х² - 4)=0 х(х-1)=0 2≠0; х² - 4 =0 х=0; х-1=0 х² = 4 х=0; х=1 х = ± 2
Cлайд 22
Пример решения квадратного уравнения Дано уравнение: Решение: Ответ:
Cлайд 23
Самостоятельная работа (по вариантам)
Cлайд 24
Проверь решение:
Cлайд 25
Проверь решение:
Cлайд 26
НАПРИМЕР Дано приведённое квадратное уравнение x²-7x+10=0 Решение: методом подбора проверим числа 2 и 5. Их произведение равно 10 (т.е. свободному члену уравнения), а их сумма равна 7, (т.е. второму коэффициенту уравнения , но с противоположным знаком ) Значит эти числа и являются корнями данного уравнения. Ответ: 2 и 5
Cлайд 27
Решить : Решаем вместе: 1) х² - 15х + 14 = 0 2) х² + 3х – 4 = 0 3) х² - 10х – 11 = 0 4) х² + 8х – 9 = 0 Решить самостоятельно в парах: 1) х² + 8х + 7 = 0 2) х² - 19х + 18 = 0 3) х² - 9х – 10 = 0 4) х² + 9х + 20 = 0
Cлайд 28
Проверим ответы: 1) х₁ =-1 х₂ =-7 2) х₁ = 1 х₂ = 18 3) х₁ =-1 х₂ =10 4) х₁ =-4 х₂ =-5
Cлайд 29
Решить самостоятельно по группам: 1) 3х² + 4х + 1 = 0, 2) 5х² - 4х – 9 = 0, 3) 6х² + 37х + 6 = 0, 4) 7х² + 2х – 5 = 0, 5) 13х² - 18х + 5 = 0, 6) 5х² + х – 6 = 0, 7) 7х² - 50х + 7 = 0, 8) 6х² - 37х + 6 = 0, 9) 7х² + 50х + 7 = 0.
Cлайд 30
Проверим:
Cлайд 31
Проверим:
Cлайд 32
Проверим:
Cлайд 33
Решить графически уравнения по вариантам: 1 вариант 1) х² + 2х – 3 = 0 2) - х² + 6х – 5 = 0 3) 2х² - 3х + 1 = 0 2 вариант 1) х² - 4х + 3 = 0 2) -х² - 3х + 4 = 0 3) 2х² - 5х + 2 = 0
Cлайд 34
Решить самостоятельно в парах: а) (х² - х)² - 14(х² - х) + 24 = 0; б) (2х - 1)⁴ - (2х - 1)² - 12 = 0 Проверим ответы: а) б)
Cлайд 35
Запомнить: Если квадратное уравнение ax²+bx+c=0 имеет корни х₁ и х₂, то квадратный трехчлен ax²+bx+c, раскладывается на множители следующим образом: ax²+bx+c= а·(х - х₁)(х - х₂).
Cлайд 36
Разложите квадратный трехчлен на множители: 1 вариант 1) х² - 11х + 24 2) х² + 7х + 12 3) - х² - 8х + 9 4) 3х² + 5х - 2 5) -5х² + 6х - 1 2 вариант 1) х² - 2х - 15 2) х² + 3х - 10 3) - х² + 5х - 6 4) 5х² + 2х - 3 5) -2х² + 9х - 4
Cлайд 37
Проверим 1 вариант 1) (х-8)(х-3) 2) (х+3)(х+4) 3) – (х-1)(х+9) 4) 3·(х-1/6)(х+13/6) 5) -5·(х-1)(х- 0,2) 2 вариант 1) (х-5)(х+3) 2) (х-2)(х+5) 3) - (х-2)(х-3) 4) 5·(х+1)(х- 0,6) 5) -2·(х-½)(х-4)
Cлайд 38
Рефлексия: Сегодня на уроке я запомнил… Сегодня на уроке я научился… Сегодня на уроке я узнал … Сегодня на уроке я выучил… Сегодня на уроке было интересно … Сегодня на уроке мне понравилось …
Cлайд 39
СПАСИБО ЗА УРОК !!!
Cлайд 40
Источники изображений http://www.avazun.ru/photoframes/&sort=&p=10 http://s59.radikal.ru/i163/0811/73/ad11fb505124.png
Cлайд 41
Cлайд 42
Cлайд 43
Cлайд 44
Cлайд 45
Cлайд 46
Cлайд 47
Cлайд 48
Cлайд 49
Cлайд 50
Cлайд 51
Cлайд 52
