X
Код презентации скопируйте его
Решение тригонометрических уравнений на интервале
Скачать эту презентацию
![2.5 Задача №3 Решить уравнение Cos²x=0,5 на интервале [3π/2; 5π/2 ]](https://bigslide.ru/images/52/51714/831/img17.jpg "2.5 Задача №3 Решить уравнение Cos²x=0,5 на интервале [3π/2; 5π/2 ]")
![2.6 Самостоятельно: Решить уравнение sin²x=0,75 на интервале [-2π; -π/2 ] ___...](https://bigslide.ru/images/52/51714/831/img18.jpg "2.6 Самостоятельно: Решить уравнение sin²x=0,75 на интервале [-2π; -π/2 ] ___...")
Презентация на тему Решение тригонометрических уравнений на интервале
Скачать эту презентациюCлайд 1
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ НА ИНТЕРВАЛЕ. Урок № 18
Cлайд 2
План урока: 1. Повторение опорного материала 1.1 Математический диктант 1.2 Знаки тригонометрических функций 1.3 Определение углов и координат точек на единичной окружности. 1.4 Формулы приведения. 2. Новый материал 2.1 Вспомним некоторые факты из жизни уравнений. 2.2 Алгоритм решения тригонометрических уравнений на интервале. 2.3 Разбор задачи. 2.4 Подсчитаем: извлечение корня. 2.5 Решение задач у доски. 2.6 Самостоятельная работа. 3. Домашнее задание 4. Подведение итогов.
Cлайд 3
Цель урока: 1. Уметь видеть и использовать нужные знания о тригонометрических функциях при решении уравнений на интервале. 2. Решать тригонометрические уравнения на интервале.
Cлайд 4
1. ПОВТОРЕНИЕ!
Cлайд 5
1.1 Математический диктант. 1. Тригонометрия - 2. Sinx – 3. Cosx – 4. Sin(-x) – 5. Cos(-x) – 6. Tg(-x) – 7. Ctg(-x) - 1. Наука, изучающая измерение углов в треугольнике. 2. ордината точки, лежащей на единичной окружности. 3. абсцисса точки, лежащей на единичной окружности. 4. - Sinx 5. Cosx 6. – Tgx 7. - Ctgx
Cлайд 6
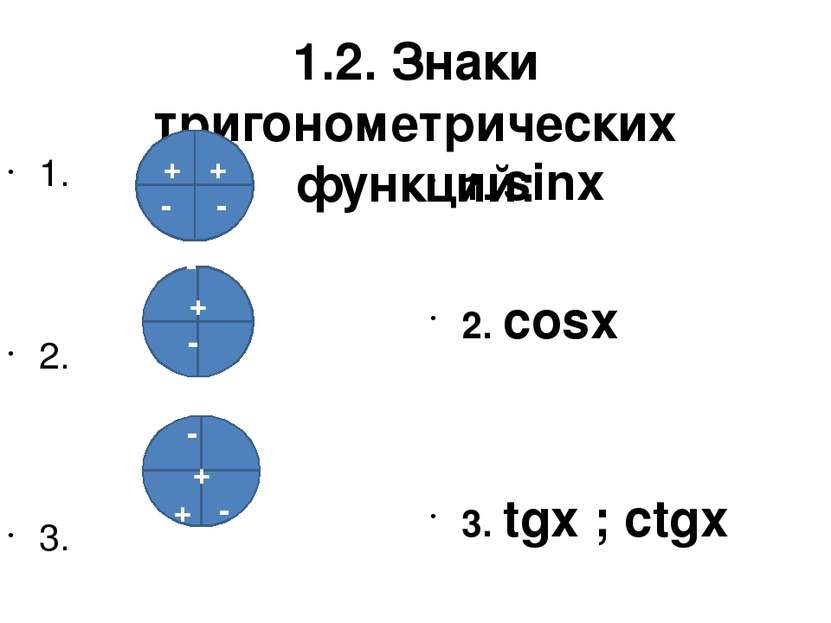
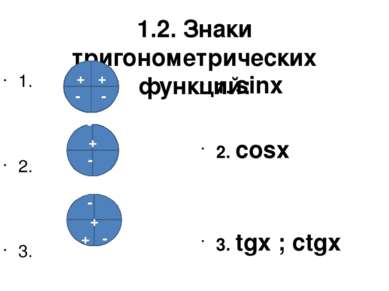1.2. Знаки тригонометрических функций: 1. 2. 3. 1. sinx 2. cosx 3. tgx ; ctgx + + - - - + - + - + + -
Cлайд 7
у 1 π/2 π 1 х -1 2π - 1 3π/2 у 1 -3π/2 -π 1 х -1 -2π -1 -π/2 0 0
Cлайд 8
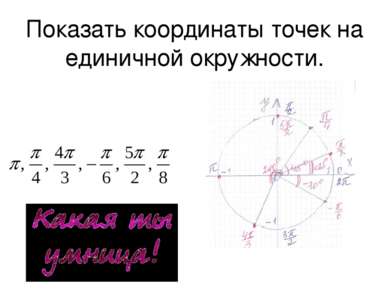
1.3. Определение углов и координат точек на единичной окружности. Определить углы, на которые опираются дуги π/6; / 30· / π/2 ; / 90· / 5π/6; / 150· / 7π/6; / 210· / 3π/2; / 270· / 11π/6 / 330· /
Cлайд 9
Показать координаты точек на единичной окружности.
Cлайд 10
1.4. Формулы приведения. ПОВТОРИМ!
Cлайд 11
2. НОВЫЙ МАТЕРИАЛ!
Cлайд 12
2.1 Вспомним: 1. Что есть уравнение? 2. Что есть х в тригонометрических функциях? 3. Наши исключения: Sinx=1 Sinx=-1 Sinx=0 Cosx=0 Cosx=1 Cosx=-1 1. Равенство, содержащее неизвестное, которое требуется найти. 2. Это аргумент, который мы и будем искать! 3. решением является: Х=π/2 + 2πn, nєZ Х=3π/2 + 2πn или х=- π/2 + 2πn, nєZ Х=πn, nєZ X=π/2 + πn, nєZ X=2πn, nєZ X=π + 2πn, nєZ
Cлайд 13
Задача №1: Рассмотрим и решим уравнение: SINX = ½ на интервале х є [ π/2 ; 2π ] 2.2 Алгоритм решения: 1. изобразим на единичной окружности данный интервал. ----------------------------------------- 2. упростим, если требуется, уравнение, т.е. приведем его к простейшему виду: sinx=a или cosx=a. ----------------------------------------------- 3. отметим значение функции на координатных осях; sinx - y или cosx – x. --------------------------------------------- 4. проведем пунктиром линию до пересечения с окружностью. ----------------------------------------- 5. отметим те точки окружности, которые попали в интервал. ----------------------------------------- 6. вычислим значения этих точек. -------------------------------------------- 7. оформим ответ.
Cлайд 14
Решение: 1. Строим единичную окружность и отмечаем данный по условию интервал. 2. уравнение уже приведено к виду sinx = a. 3.Отмечаем на оси оу значение ½. 4. проводим пунктиром линию до пересечения с окружностью через точку у=1/2. 5. Видим, что в данный интервал попало только одно значение х1. 6. Производим расчет х1: Х1 = π – π/6 = 5π/6. Точка х2 = π/6 не принадлежит интервалу [π/2; 2π] 7. Ответ: х1 = 5π/6
Cлайд 15
2.3 Задача №2. Рассмотрим и решим уравнение: SINX = ½ на интервале х є [ -2π ; -3π/2 ] _____________________ Решение. Х1=-2π + π/6=-11π/6 Ответ: х1=-11π/6
Cлайд 16
2.4 Посчитаем: извлечем корень. 3/4 1/2 2 3 1/9 1/3 0 1
Cлайд 17
Cлайд 18
![2.5 Задача №3 Решить уравнение Cos²x=0,5 на интервале [3π/2; 5π/2 ]](https://bigslide.ru/images/52/51714/960/img17.jpg "2.5 Задача №3 Решить уравнение Cos²x=0,5 на интервале [3π/2; 5π/2 ]")
2.5 Задача №3 Решить уравнение Cos²x=0,5 на интервале [3π/2; 5π/2 ]
Cлайд 19
![2.6 Самостоятельно: Решить уравнение sin²x=0,75 на интервале [-2π; -π/2 ] ___...](https://bigslide.ru/images/52/51714/960/img18.jpg "2.6 Самостоятельно: Решить уравнение sin²x=0,75 на интервале [-2π; -π/2 ] ___...")
2.6 Самостоятельно: Решить уравнение sin²x=0,75 на интервале [-2π; -π/2 ] _____________________ Решение: Х1=-2π+π/3=-5π/3 Х2=-π-π/3=-4π/3 Х3=-π+π/3=-2π/3 _________________________
Cлайд 20
3. Домашнее задание.
Cлайд 21
4. Итак оценим свою работу. 25 и более балов 18-24 балов Менее 17 балов Оценка «5». Оценка «4». Оценка «3».
Cлайд 22
