X
Код презентации скопируйте его
Параллельные прямые в пространстве
Скачать эту презентацию
Презентация на тему Параллельные прямые в пространстве
Скачать эту презентациюCлайд 1
МБОУ- СОШ № 7 х. Новоселовка Мартыновский район Ростовская область Параллельные прямые в пространстве Составитель: Смирнова Светлана Викторовна, учитель математики
Cлайд 2
Параллельные прямые в пространстве
Cлайд 3
«Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» Леонардо да Винчи
Cлайд 4
Параллельные прямые в пространстве
Cлайд 5
Цели урока: Рассмотреть взаимное расположение двух прямых в пространстве; Ввести понятие параллельных и скрещивающихся прямых 2) Доказать теоремы о параллельности прямых и параллельности трех прямых; 3) Закрепить эти понятия на моделях куба, призмы. пирамиды
Cлайд 6
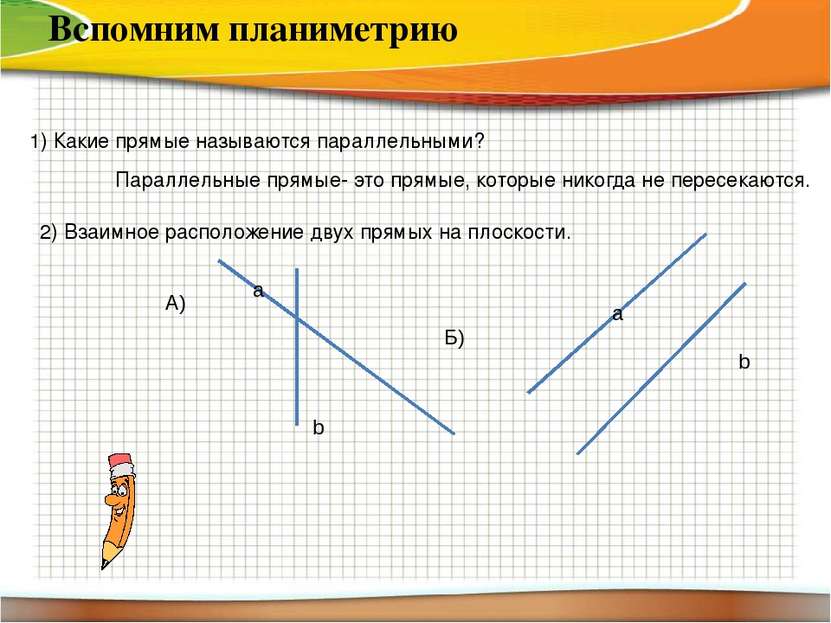
Вспомним планиметрию 1) Какие прямые называются параллельными? Параллельные прямые- это прямые, которые никогда не пересекаются. 2) Взаимное расположение двух прямых на плоскости. a b А) Б) a b
Cлайд 7
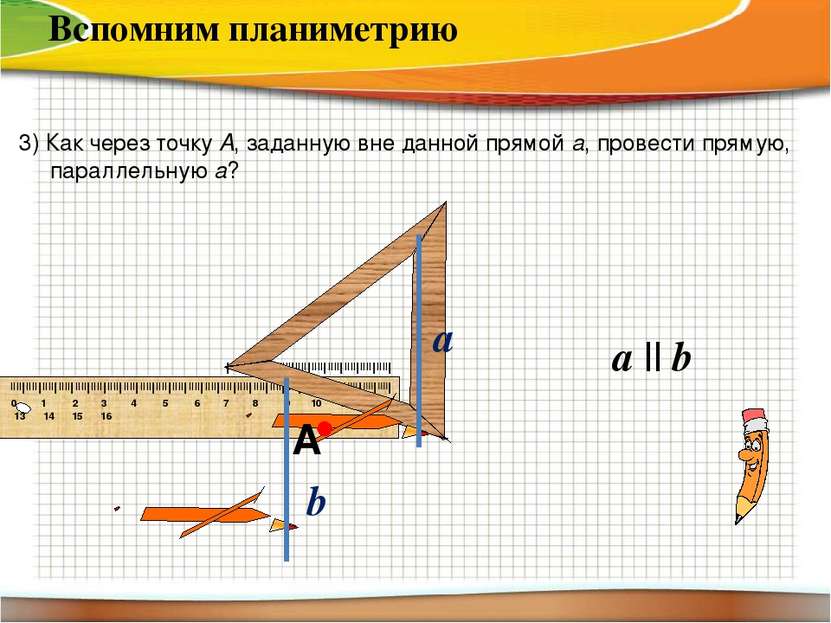
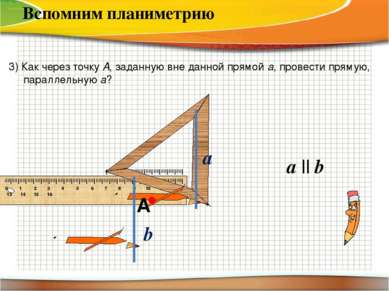a || b 3) Как через точку A, заданную вне данной прямой a, провести прямую, параллельную а? Вспомним планиметрию А a b
Cлайд 8
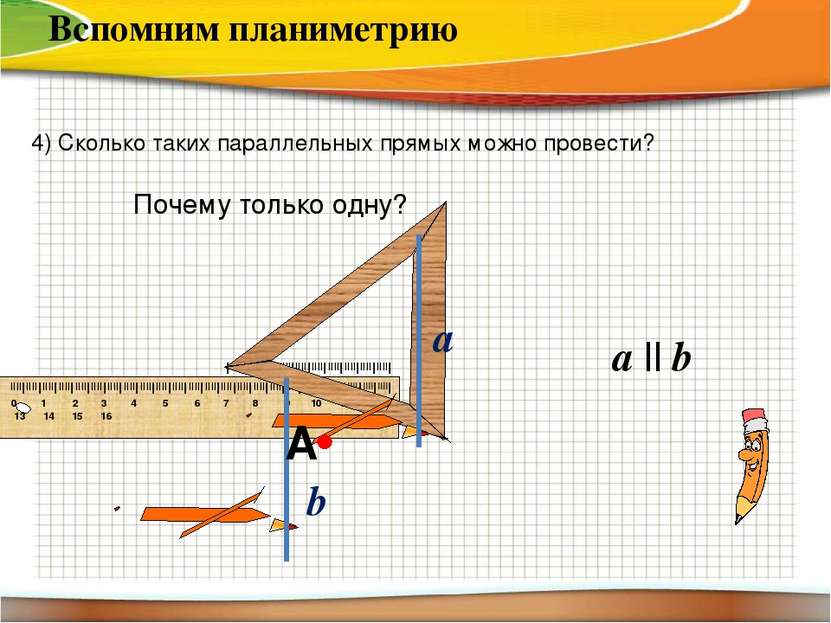
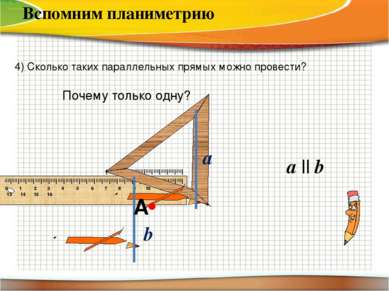a || b 4) Сколько таких параллельных прямых можно провести? Вспомним планиметрию А Почему только одну? a b
Cлайд 9
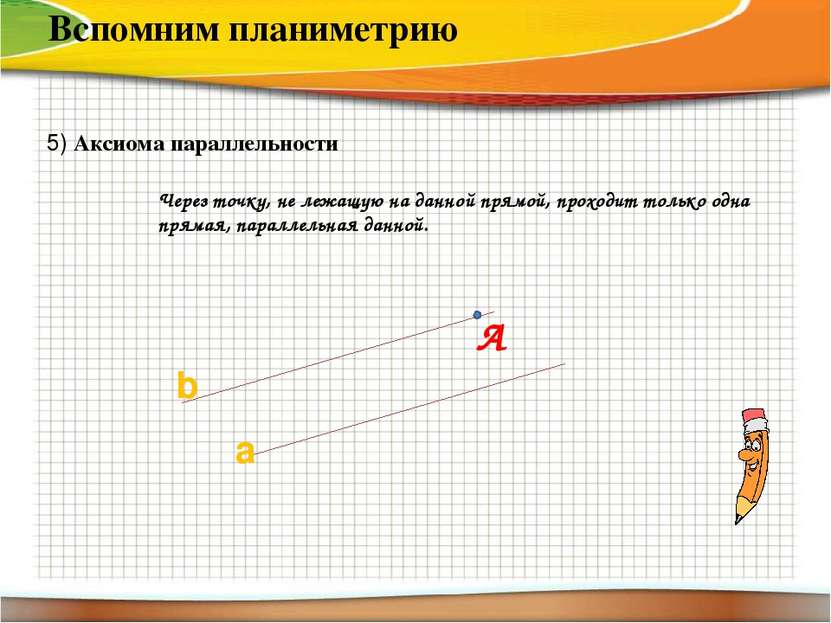
5) Аксиома параллельности Вспомним планиметрию Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. а b А
Cлайд 10
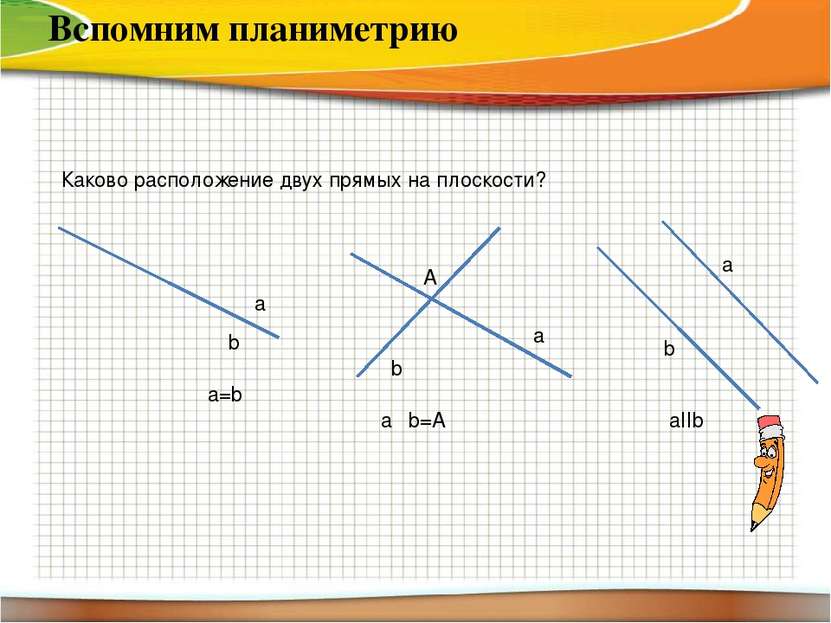
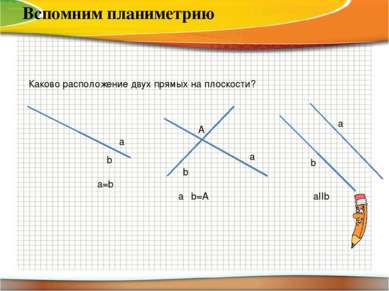Каково расположение двух прямых на плоскости? a b b a a b a=b aΩb=A A aІІb Вспомним планиметрию
Cлайд 11
Перейдём в пространство А А Пересекаются в одной точке.
Cлайд 12
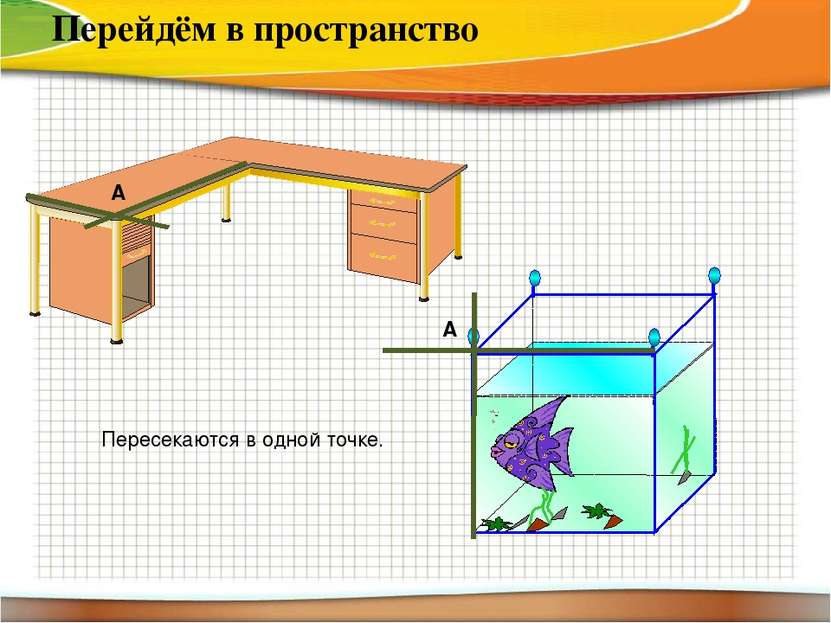
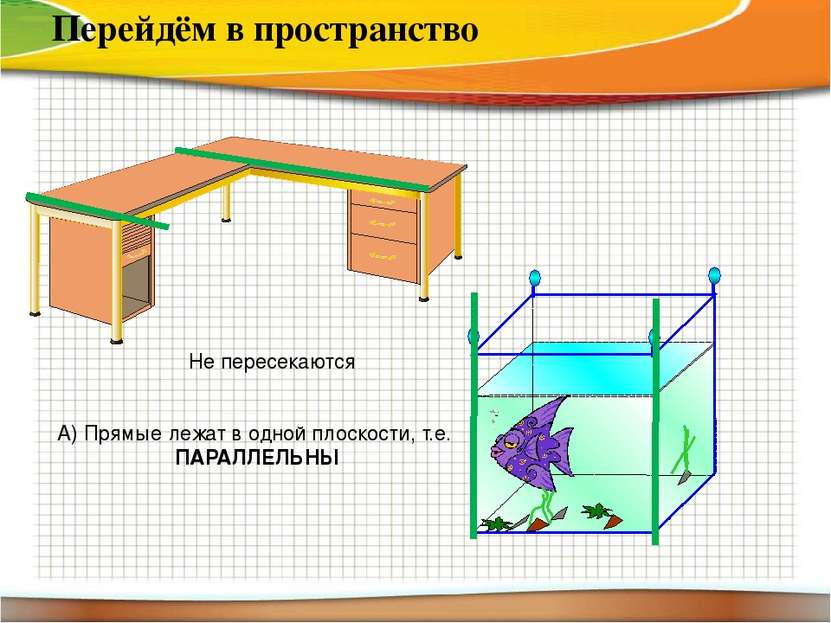
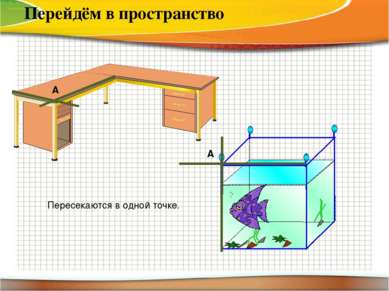
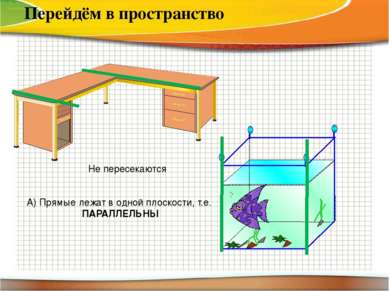Перейдём в пространство Не пересекаются А) Прямые лежат в одной плоскости, т.е. ПАРАЛЛЕЛЬНЫ
Cлайд 13
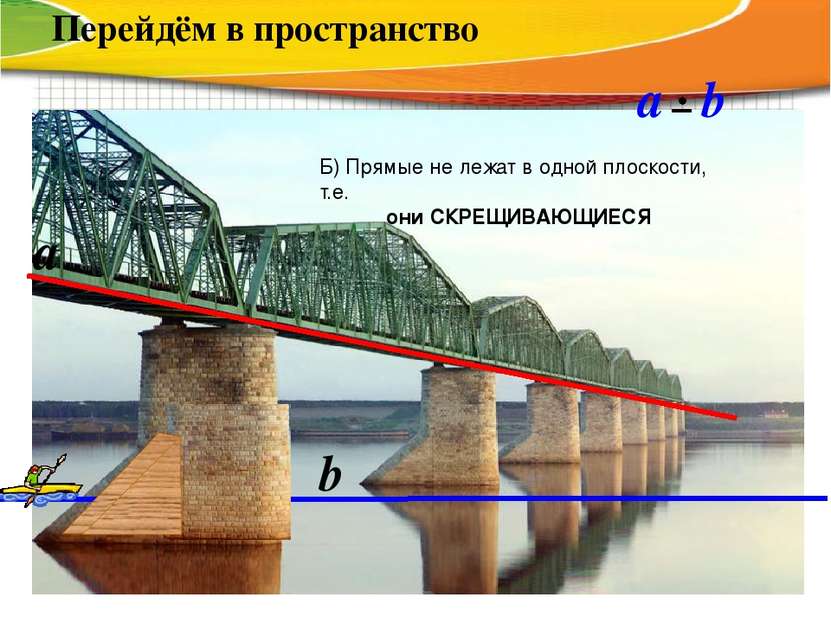
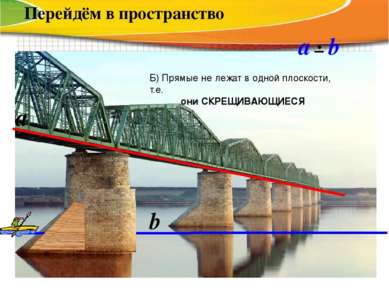a b Перейдём в пространство Б) Прямые не лежат в одной плоскости, т.е. они СКРЕЩИВАЮЩИЕСЯ a b
Cлайд 14
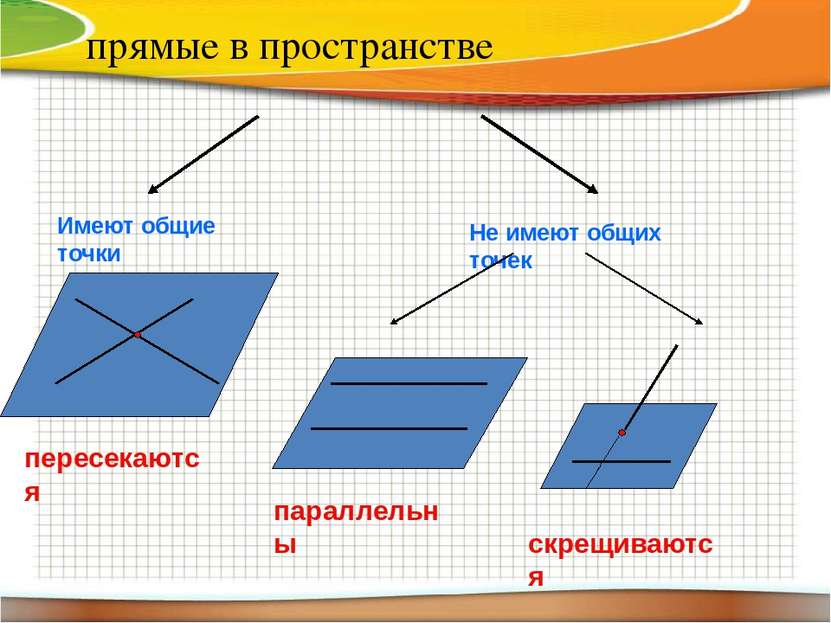
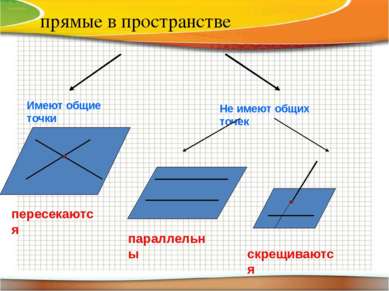прямые в пространстве Имеют общие точки Не имеют общих точек пересекаются параллельны скрещиваются
Cлайд 15
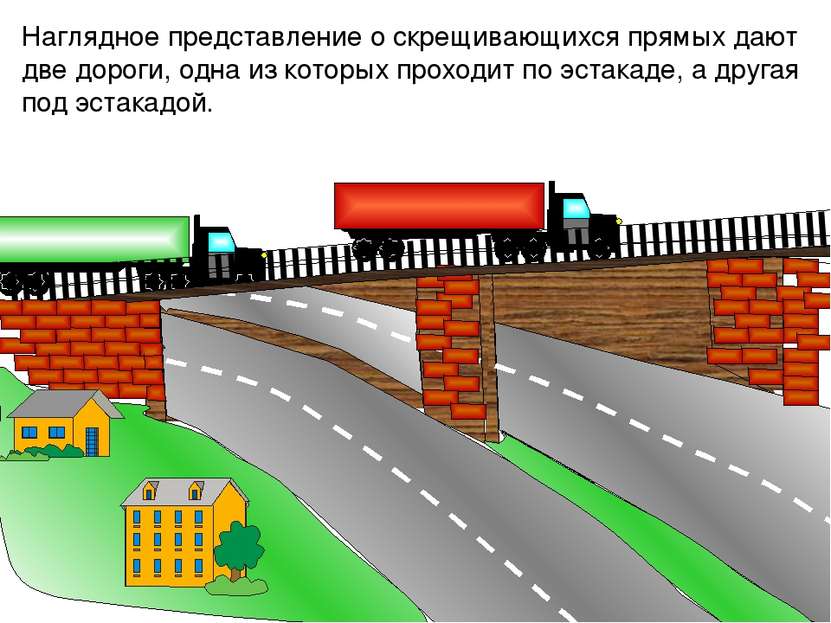
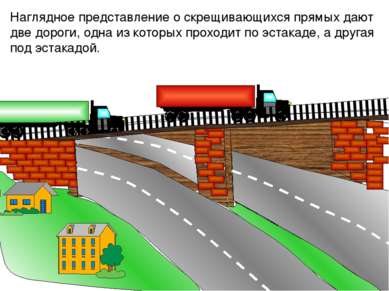IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.
Cлайд 16
Cлайд 17
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. №803. Математика 5 класс. Н.Я.Виленкин.
Cлайд 18
Через точку вне данной прямой в пространстве можно провести прямую параллельную данной и притом только одну. Дано: прямая а, А Є а Доказать : Провести через А пряму b || a, b единственна Теорема А а
Cлайд 19
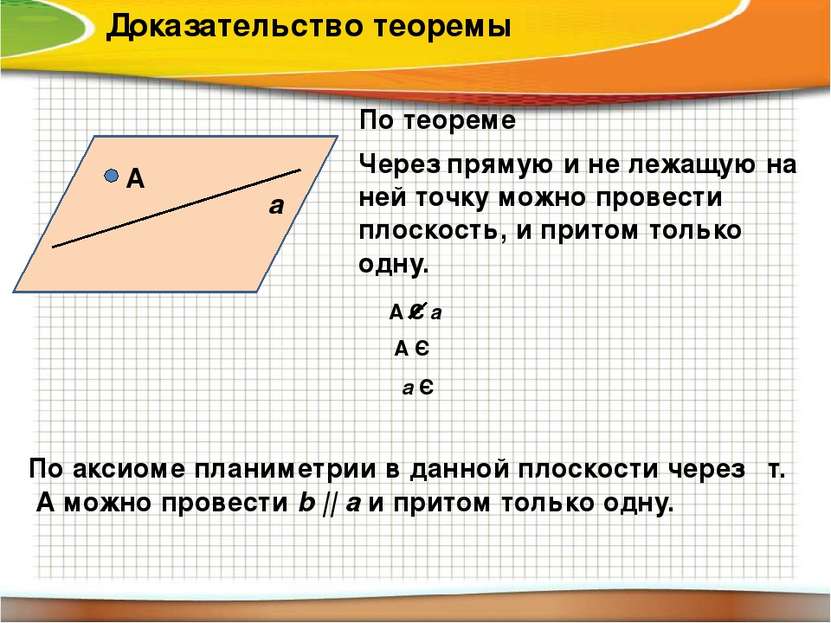
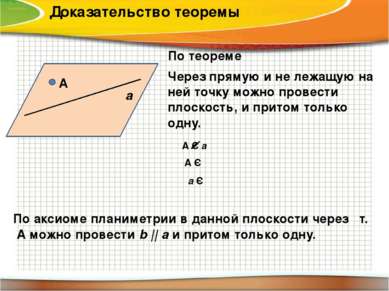Доказательство теоремы По теореме Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. А а α А Є а А Є α a Є α По аксиоме планиметрии в данной плоскости через т. А можно провести b || a и притом только одну.
Cлайд 20
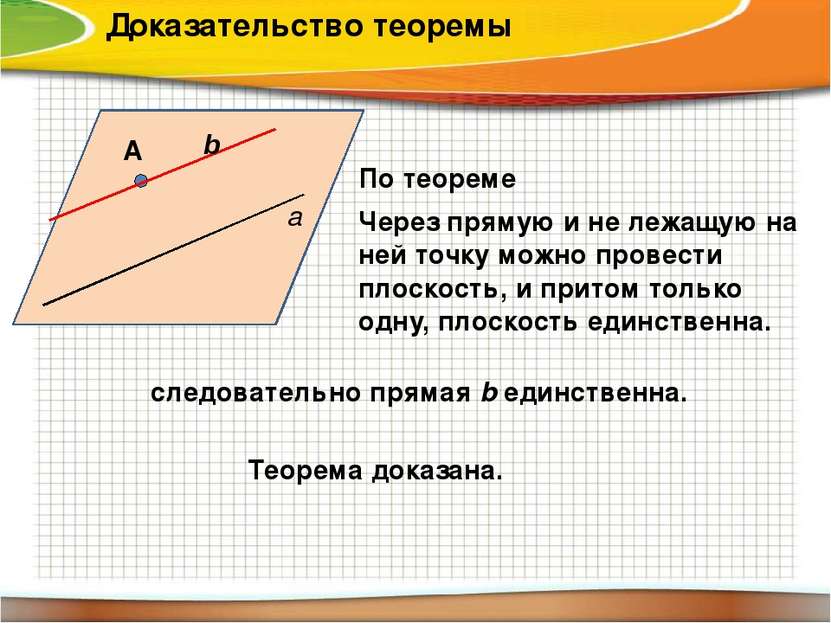
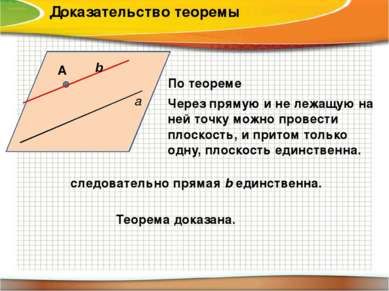Доказательство теоремы следовательно прямая b единственна. Теорема доказана. а А α По теореме Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну, плоскость единственна. b
Cлайд 21
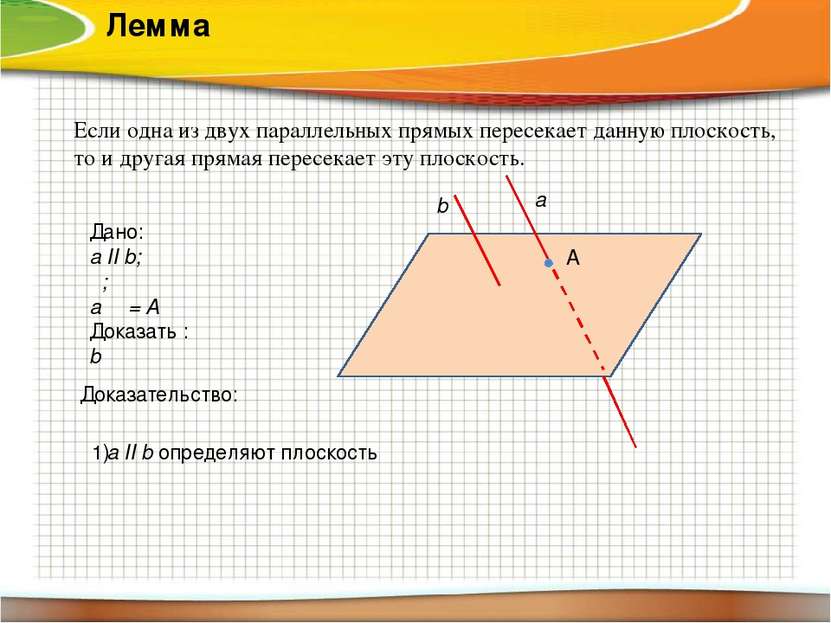
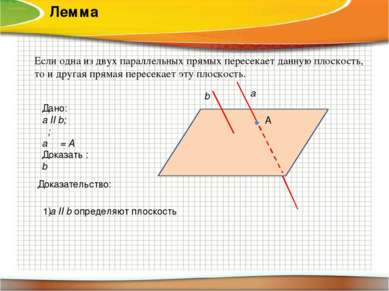Лемма Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Дано: a ІІ b; α; aΩα= A Доказать : bΩα α a b А Доказательство: 1) a ІІ b определяют плоскость β
Cлайд 22
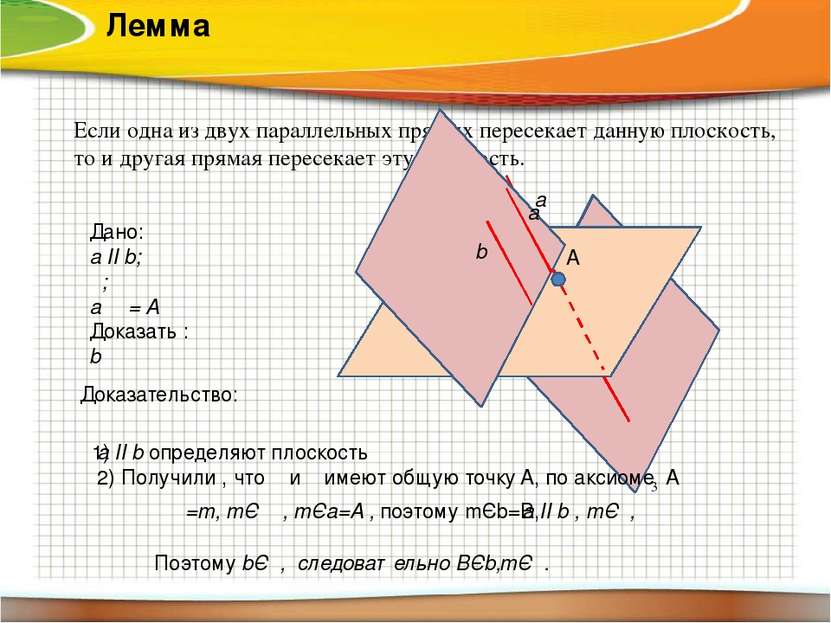
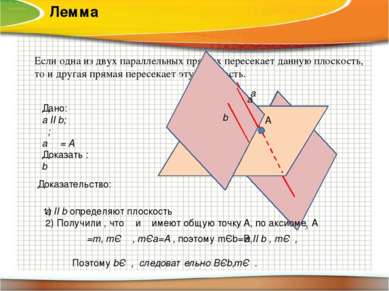Лемма Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Дано: a ІІ b; α; aΩα= A Доказать : bΩα Доказательство: 1) a ІІ b определяют плоскость β 2) Получили , что α и β имеют общую точку A, по аксиоме А α a b А a b β 3 αΩ β =m, mЄ β , mЄa=A , поэтому mЄb=B, a ІІ b , mЄα, Поэтому bЄα, следовательно BЄb, mЄα.
Cлайд 23
признак параллельности прямых в пространстве. Если две прямые параллельны третьей прямой, то они тоже параллельны Дано: а||b; c||b Доказать : a||c Теорема 16.2 a b c
Cлайд 24
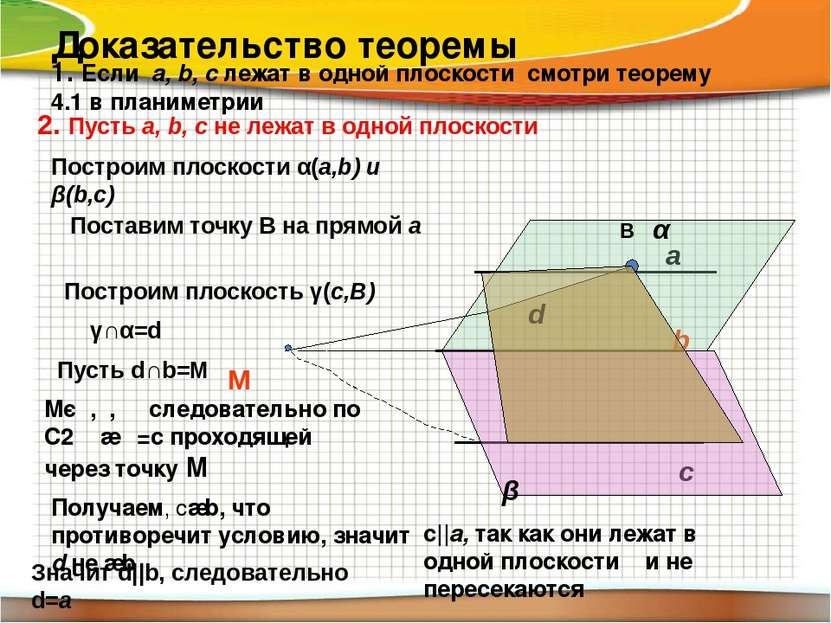
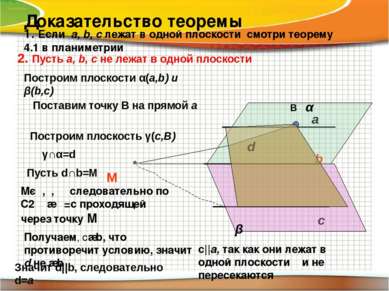Доказательство теоремы 1. Если a, b, c лежат в одной плоскости смотри теорему 4.1 в планиметрии Mєα,γ, β следовательно по С2 γ∩β =с проходящей через точку М Получаем, c∩b, что противоречит условию, значит d не ∩b c||a, так как они лежат в одной плоскости γ и не пересекаются 2. Пусть a, b, c не лежат в одной плоскости a b c Построим плоскости α(a,b) и β(b,c) α β Поставим точку В на прямой а В Построим плоскость γ(с,В) γ∩α=d d Пусть d∩b=M M Значит d||b, следовательно d=а
Cлайд 25
Закрепление изученного материала Задача № 17 D B C A M N P Q Дано: М- середина BD, N- середина CD, Q- середина AC, P- середина AB, AD= 12, DC= 14 Найти: P MNPQ Решение: 1. MNІІ BC по составу средней линии MN II PQ; PQ IIDA 2. PMIIAD по составу средней линии PMIIQN; NQIIDA 3. По определению MNQP -параллелограмм 4. PQ=7; PM= 6 P = 2(7+6)=26 MNPQ Ответ: 26
Cлайд 26
Домашнее задание: Пункт 4-5, теоремы, задача № 16
Cлайд 27
Спасибо за урок.
