X
Код презентации скопируйте его
Математический анализ
Скачать эту презентацию
Презентация на тему Математический анализ
Скачать эту презентациюCлайд 1
Глава 3. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА 3.1 Принятые обозначения числовых множеств Сегменты ( замкнутые множества) Интервалы (открытые множества) Интервалы полуоткрытые полуинтервалы
Cлайд 2
Cлайд 3
3.2 Предел функции в точке и на бесконечности
Cлайд 4
3.3 Первый и второй замечательные пределы Первый замечательный предел Второй замечательный предел Часто используются следующие следствия:
Cлайд 5
3.4 Бесконечно малые и бесконечно большие функции.
Cлайд 6
3.5. Некоторые эквивалентные бесконечно малыми функции Данное определение особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене одной бесконечно малой величины на другую, эквивалентную ей. Найдём предел Так как tg5x ~ 5x и sin7x ~ 7x при х 0, то, заменив функции эквивалентными бесконечно малыми, получим: Пример 1 1 1 1 1 1 1
Cлайд 7
3.6 Раскрытие неопределенностей. К разряду неопределенностей принято относить следующие соотношения: Задача . Найти пределы . 1) 4) Задача . Найти пределы 3)
Cлайд 8
3.7 Непрерывность функции в точке. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е. . Локальные свойства непрерывных функций. Точка х0 называется точкой разрыва первого рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы: Точка х0 называется точкой разрыва второго рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен. 3.8 Точки разрыва, их классификация.
Cлайд 9
3.9. Асимптоты функции. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю. Функция существует всюду, кроме точки x=0, т.е. на интервалах (- , 0) и (0,+ ) = > x=0 является точкой разрыва 2-го рода, так как Пример 1 1 1 1 1 1 1. , Найти асимптотs функции если они существуют. Наклонная асимптота имеет уравнение у=х.
Cлайд 10
Cлайд 11
Глава4. Дифференциальное исчисление функции одной переменной Тема 4.1 Определение производной. Геометрический и механический смысл производной Основные правила дифференцирования. Производная сложной функции. Тема 4.2 Производные элементарных функций. Производная функций, заданных неявно и параметрически. Производные высших порядков Карл Фридрих Гаусс – родился 30 апреля 1977 года в Германии. Считается "королём математики". Занимался исследованиями в таких областях как: алгебра, дифференциальная и неевклидовая геометрия, математический анализ, теории функций комплексного переменного, теория вероятностей, а также в астрономии, геодезии и механике.
Cлайд 12
4.1 Определение производной. Так как последние соотношения cправедливы в любой «текущей » точке x, получаем
Cлайд 13
4.2. Геометрический и физический смысл производной Производная функции в точке равна тангенсу угла наклона касательной к кривой в этой точке
Cлайд 14
4.3 Таблица производных элементарных функций
Cлайд 15
4.4 Основные правила дифференцирования
Cлайд 16
Р Е Ш Е Н И Е
Cлайд 17
Cлайд 18
Пусть функция y= f(x)- дифференцируема на некотором интервале. Дифференцируя ее, получим первую производную Если найти производную первой производной f (x), получим вторую производную функции f(x) Последовательно продолжая этот процесс можно найти производную функции порядка n как производную функции порядка (n-1) 4.5.
Cлайд 19
4.6. Формула Тейлора , При а = 0 формула Тейлора называется формулой Маклорена. ,
Cлайд 20
4.7. Разложение основных элементарных функций по формуле Маклорена.
Cлайд 21
Найти область определения функции Установить тип функции (чётность, нечётность, периодичность) Найти точки разрыва функции и интервалы непрерывности Установить характер точек разрыва функции Найти и построить (пунктиром) асимптоты функции Найти точки пересечения графика функции c осями координат. Найти интервалы положительности и отрицательности функции Найти интервалы монотонности функции Найти интервалы выпуклости функции Построить график функции Анри Пуанкаре - Выдающийся французский учёный. Математик, физик, философ, астроном, Родился 29 апреля, 1854 года. Являлся членом более 30 академий мира. Известен как один из создателей топологии и теории относительности. - 4. 8. Алгоритм исследования функции одного аргумента
Cлайд 22
●Область определения, периодичность, чётность.
Cлайд 23
● Интервалы монотонности функции (интервалы знакопостоянства первой производной) Точки экстремума функции (точки минимума и максимума функции) Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1). Если при переходе через точку х1 слева направо производная функции f (x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то точке х = х1 функция имеет минимум.
Cлайд 24
Ymin(2)=3. Функция возрастает на интервалах (- , 0) и (2,+ ), убывает на интервале (0,2). Пример 1
Cлайд 25
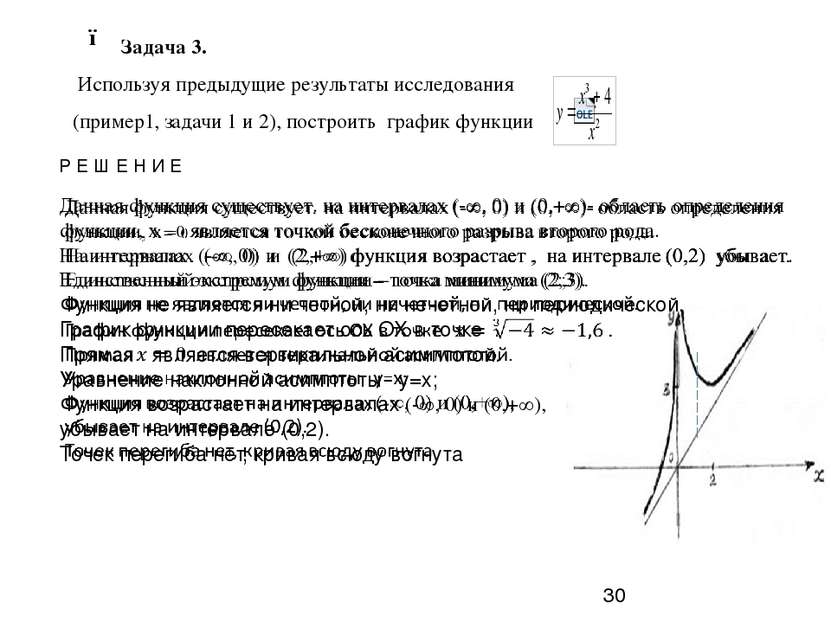
Пример 2 . Исследуем на экстремум функцию Р Е Ш Н И Е Так как х=0 не принадлежит области определения функции, поэтому точек перегиба нет Кривая всюду вогнута.
Cлайд 26
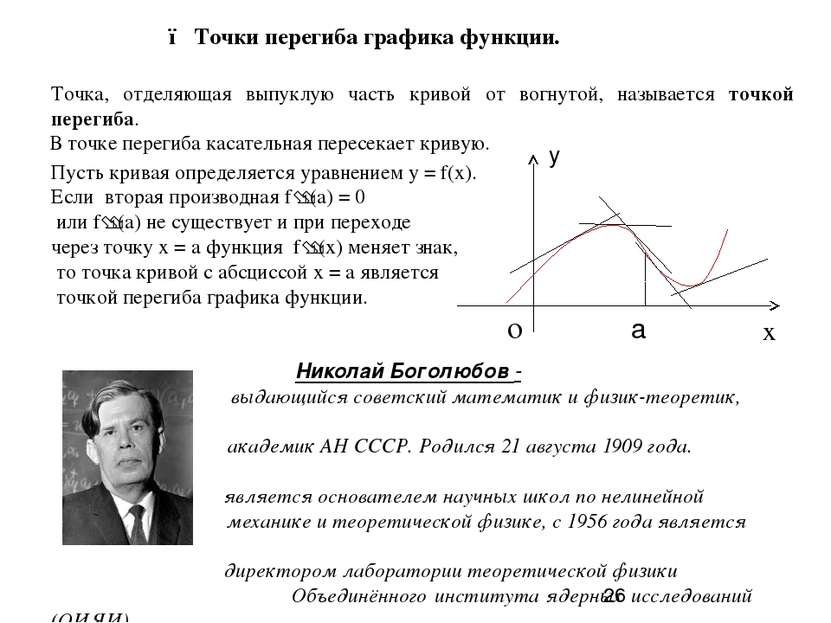
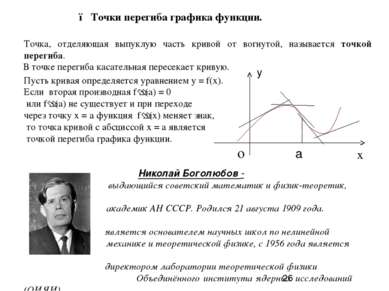● Точки перегиба графика функции. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. В точке перегиба касательная пересекает кривую. Пусть кривая определяется уравнением y = f(x). Если вторая производная f (a) = 0 или f (a) не существует и при переходе через точку х = а функция f (x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба графика функции. Николай Боголюбов - выдающийся советский математик и физик-теоретик, академик АН СССР. Родился 21 августа 1909 года. является основателем научных школ по нелинейной механике и теоретической физике, с 1956 года является директором лаборатории теоретической физики Объединённого института ядерных исследований (ОИЯИ) в Дубне, с 1965 по 1988 год являлся директором ОИЯИ. y x о а
Cлайд 27
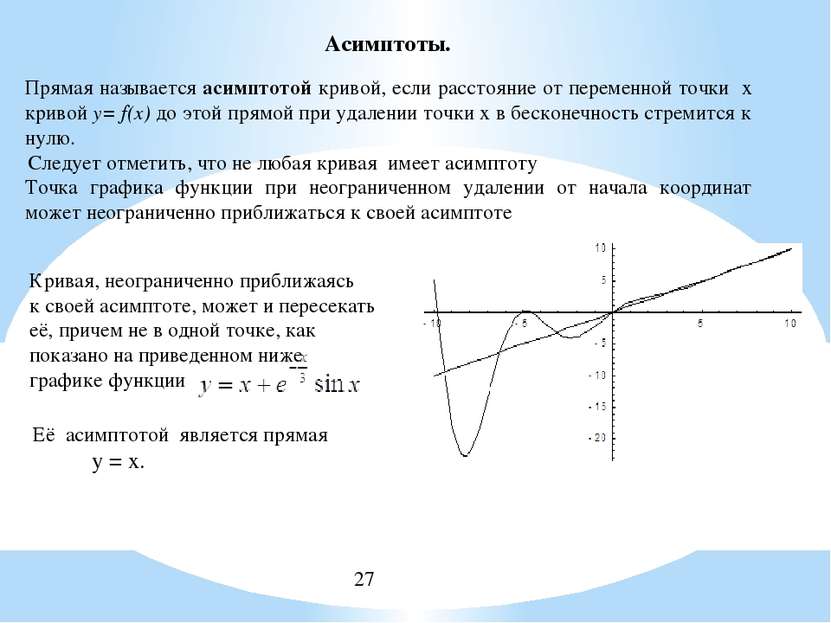
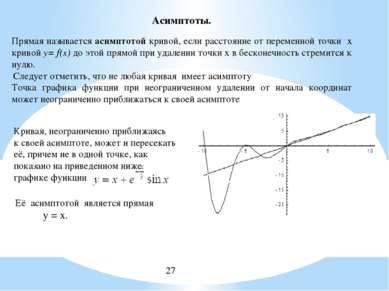Асимптоты. Прямая называется асимптотой кривой, если расстояние от переменной точки x кривой y= f(x) до этой прямой при удалении точки x в бесконечность стремится к нулю. Точка графика функции при неограниченном удалении от начала координат может неограниченно приближаться к своей асимптоте Следует отметить, что не любая кривая имеет асимптоту Кривая, неограниченно приближаясь к своей асимптоте, может и пересекать её, причем не в одной точке, как показано на приведенном ниже графике функции Её асимптотой является прямая у = х.
Cлайд 28
А) вертикальные асимптоты Если или или то прямая х = а является асимптотой кривой y = f(x). Задача 1. Найти уравнения вертикальных асимптот функции Данная функция существует всюду, кроме точки Х=0, т.е. на интервалах (- , 0) (0,+ ). Точка Х=0 является точкой разрыва второго рода, так как ,
Cлайд 29
В) Наклонные асимптоты Наклонная асимптота имеет уравнение Р е ш е н и е Уравнение наклонной асимптоты: у = х. Задача 2. Найти уравнения наклонных асимптот графика функции . . , где
Cлайд 30
● Задача 3. Используя предыдущие результаты исследования (пример1, задачи 1 и 2), построить график функции Р Е Ш Е Н И Е
