X
Код презентации скопируйте его
Объём тел
Скачать эту презентацию
Презентация на тему Объём тел
Скачать эту презентациюCлайд 1
МОУ «Средняя общеобразовательная школа с. Погорелка Шадринский район Курганская область Учитель математики первой квалификационной категории Кощеев М.М.
Cлайд 2
ПЛОСКИЕ ОБЪЕМНЫЕ
Cлайд 3
ПЛОСКИЕ ФИГУРЫ ТРЕУГОЛЬНИК КВАДРАТ ПРЯМОУГОЛЬНИК КРУГ ЧЕТЫРЕХУГОЛЬНИК
Cлайд 4
КУБ ЦИЛИНДР ПАРАЛЛЕПИПЕД
Cлайд 5
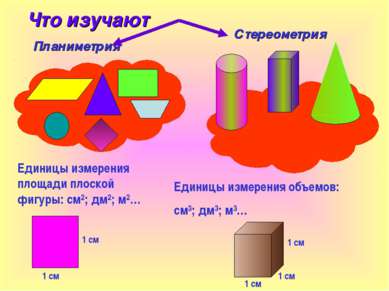Планиметрия Стереометрия Единицы измерения площади плоской фигуры: см²; дм²; м²… 1 см 1 см Единицы измерения объемов: см³; дм³; м³… 1 см 1 см 1 см Что изучают
Cлайд 6
Cлайд 7
Цель урока: Изучить с учащимися теорему об объеме цилиндра; Выработать навыки решения задач с использованием формулы объема цилиндра;
Cлайд 8
Цели : Развитие логического мышления, пространственного воображения, умений действовать по алгоритму, составлять алгоритмы действий. Воспитание познавательной активности, самостоятельности.
Cлайд 9
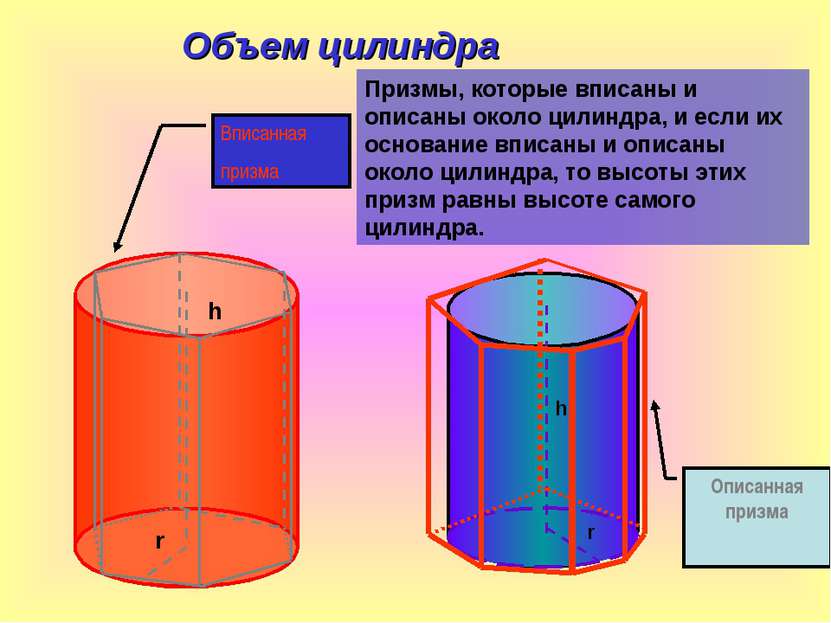
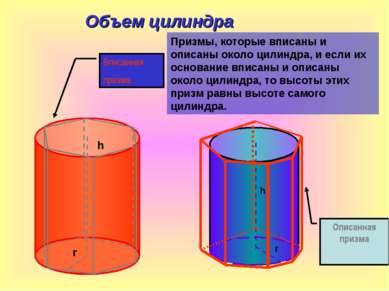Объем цилиндра Призмы, которые вписаны и описаны около цилиндра, и если их основание вписаны и описаны около цилиндра, то высоты этих призм равны высоте самого цилиндра. h r h r Вписанная призма Описанная призма
Cлайд 10
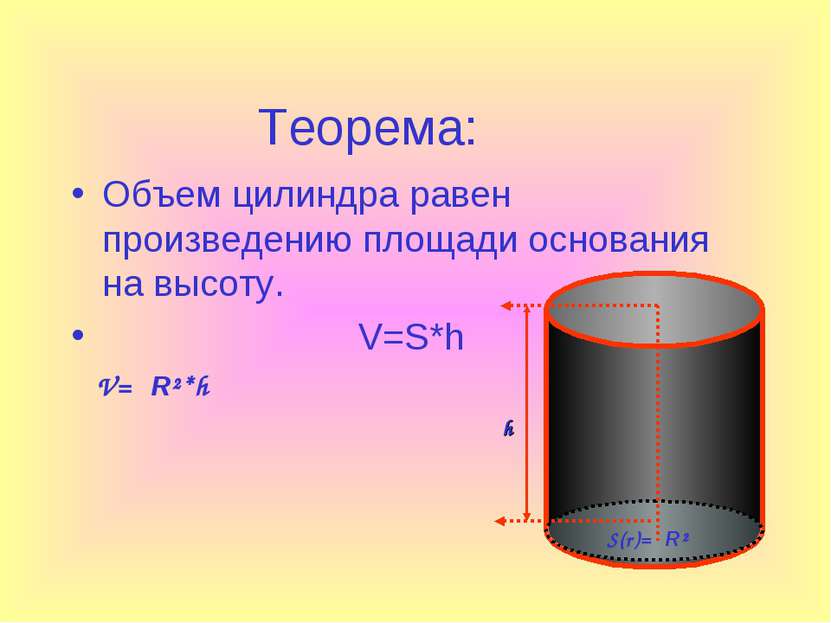
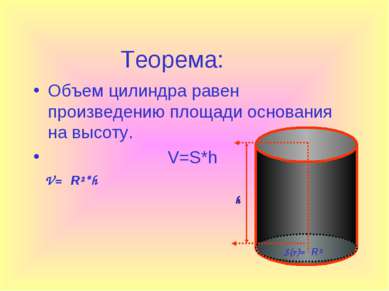Теорема: Объем цилиндра равен произведению площади основания на высоту. V=S*h V=πR²*h S(r)=πR² h
Cлайд 11
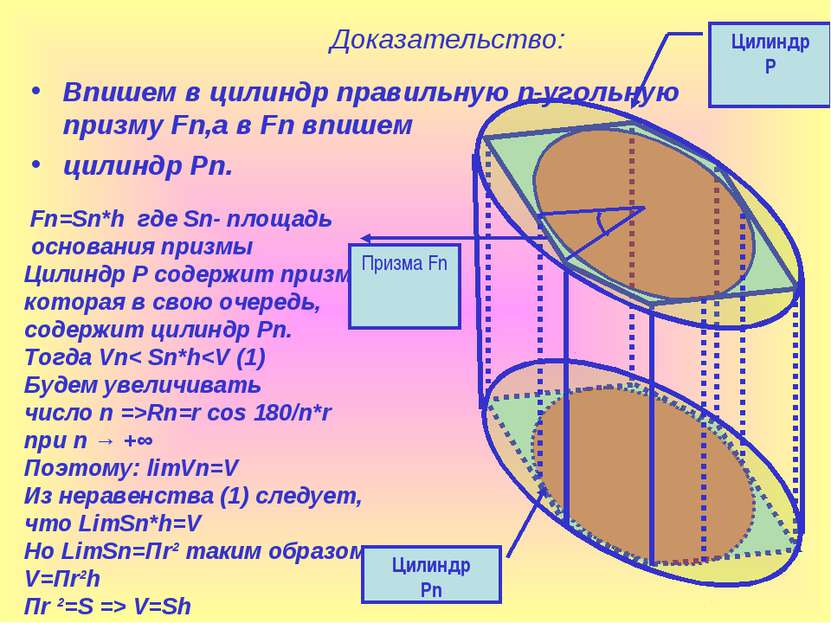
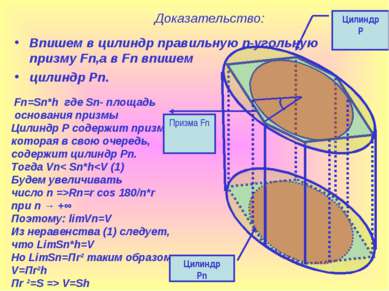Доказательство: Впишем в цилиндр правильную n-угольную призму Fn,а в Fn впишем цилиндр Pn. Fn=Sn*h где Sn- площадь основания призмы Цилиндр Р содержит призму Fn, которая в свою очередь, содержит цилиндр Pn. Тогда Vn< Sn*hRn=r cos 180/n*r при n → +∞ Поэтому: limVn=V Из неравенства (1) следует, что LimSn*h=V Но LimSn=Пr² таким образом V=Пr²h Пr ²=S => V=Sh Цилиндр P Цилиндр Pn Призма Fn
Cлайд 12
Свойство объемов №1 Равные тела имеют равные объемы Свойство объемов №2 Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел. Свойство объемов №3 Если одно тело содержит другое, то объем первого тела не меньше объема второго.
Cлайд 13
Зад. № 671г) Дано: Цилиндр, вписанная n-угольная призма, n=8. Найти: Vпр./ Vцил. Решение:
Cлайд 14
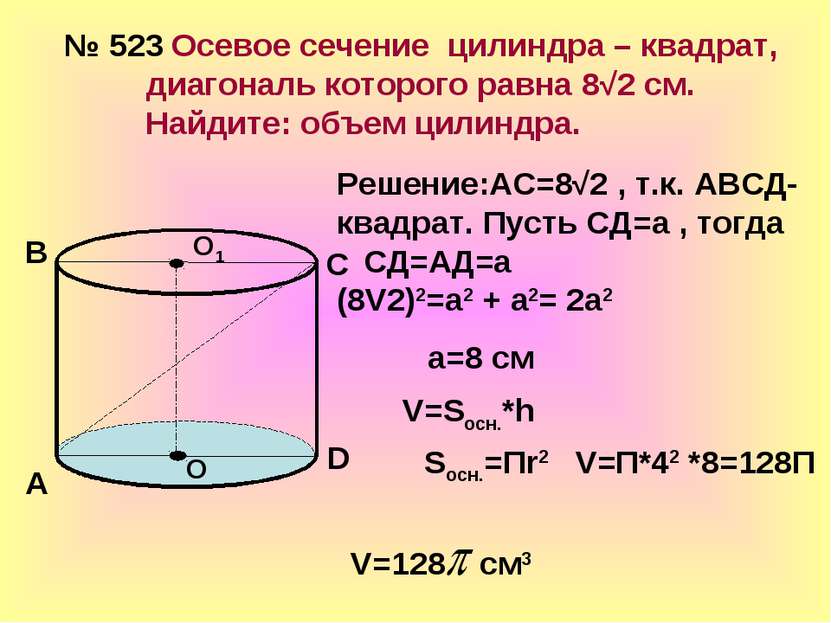
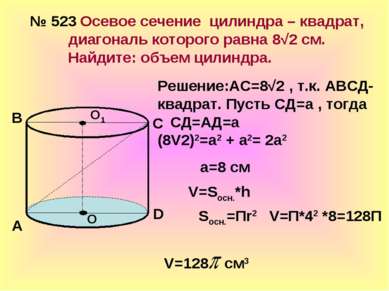№ 523 Осевое сечение цилиндра – квадрат, диагональ которого равна 8√2 см. Найдите: объем цилиндра. О О1 А В С D Решение:АС=8√2 , т.к. АВСД- квадрат. Пусть СД=а , тогда СД=АД=а (8V2)2=а2 + а2= 2а2 а=8 см V=Sосн.*h Sосн.=Пr2 V=П*42 *8=128П V=128 см3
Cлайд 15
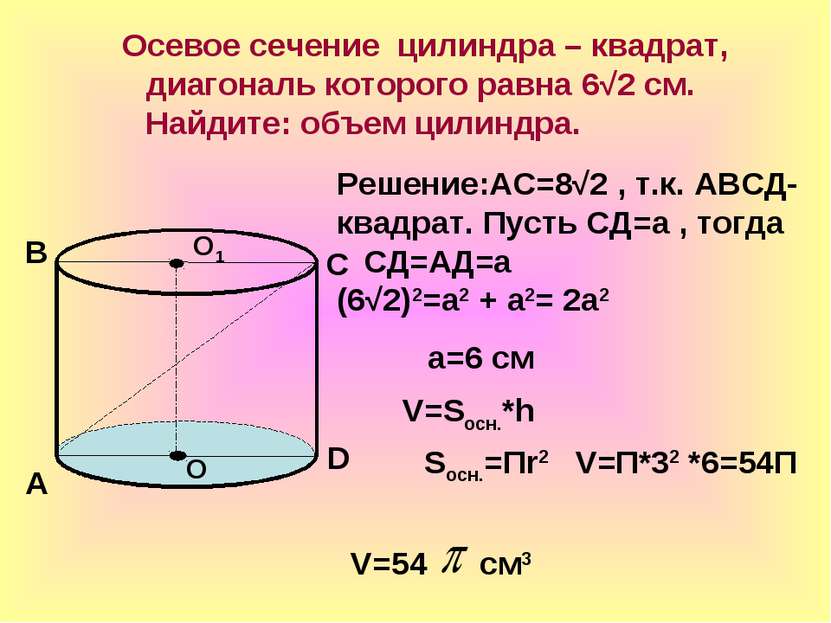
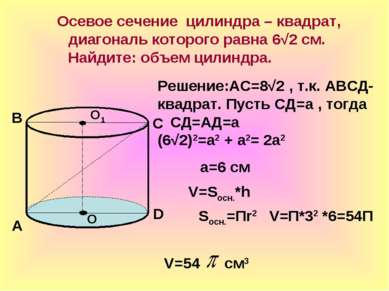Осевое сечение цилиндра – квадрат, диагональ которого равна 6√2 см. Найдите: объем цилиндра. О О1 А В С D Решение:АС=8√2 , т.к. АВСД- квадрат. Пусть СД=а , тогда СД=АД=а (6√2)2=а2 + а2= 2а2 а=6 см V=Sосн.*h Sосн.=Пr2 V=П*32 *6=54П V=54 см3
Cлайд 16
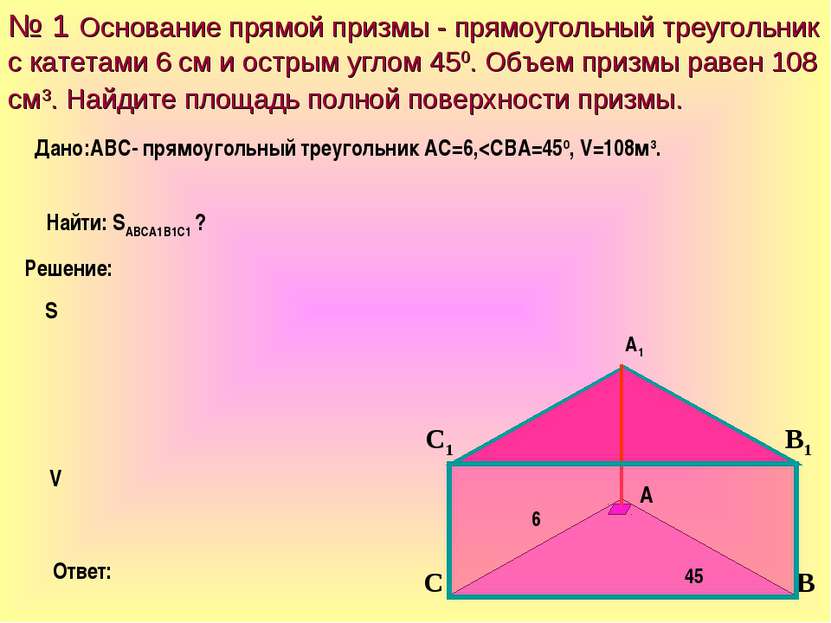
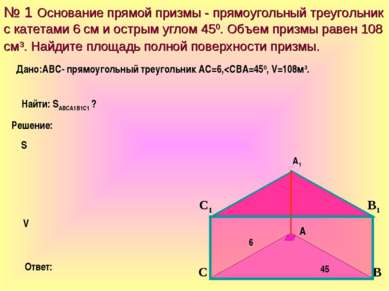№ 1 Основание прямой призмы - прямоугольный треугольник с катетами 6 см и острым углом 450. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы. Решение: Ответ: S Найти: SАВСА1В1С1 ? Дано:АВС- прямоугольный треугольник АС=6,
Cлайд 17
Домашнее задание П.74,75,76,77 № 666 б, 669, 671 а,б
Cлайд 18
Библиография Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев «Геометрия, 10-11», М., Просвещение, 2007 В.Я. Яровенко «Поурочные разработки по геометрии», Москва, «ВАКО», 2006
Cлайд 19
