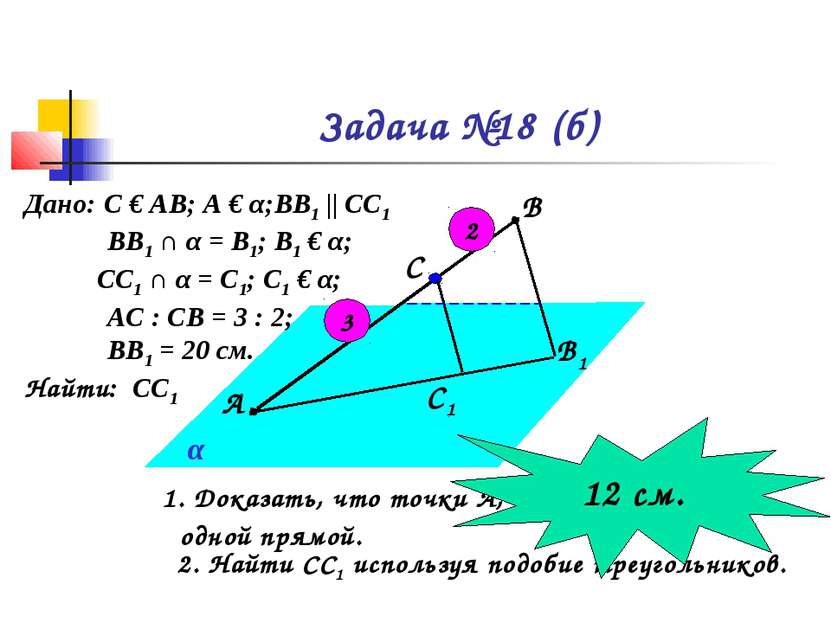
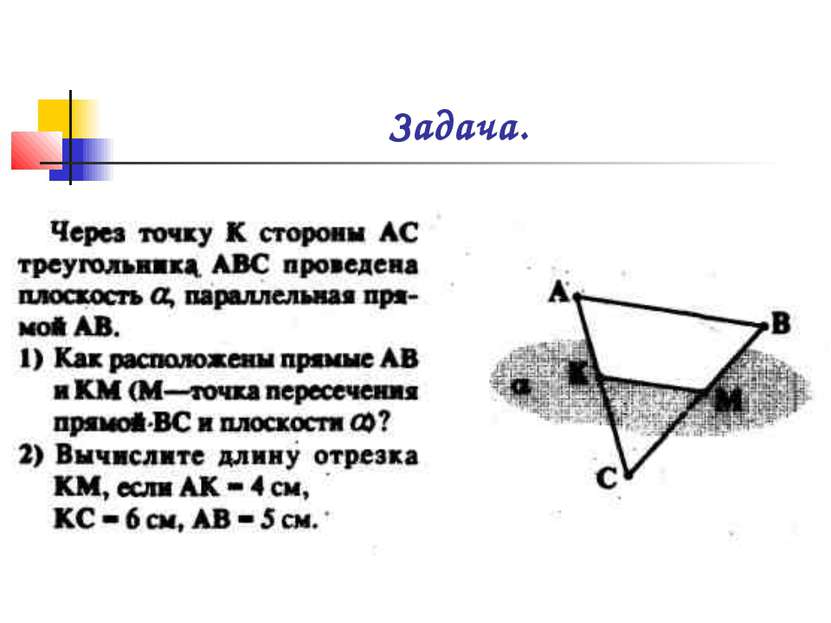
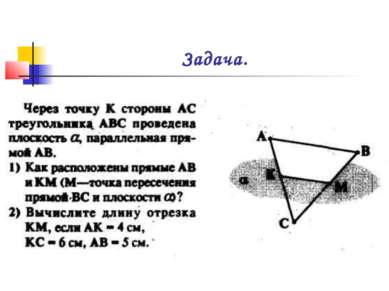
X
Код презентации скопируйте его
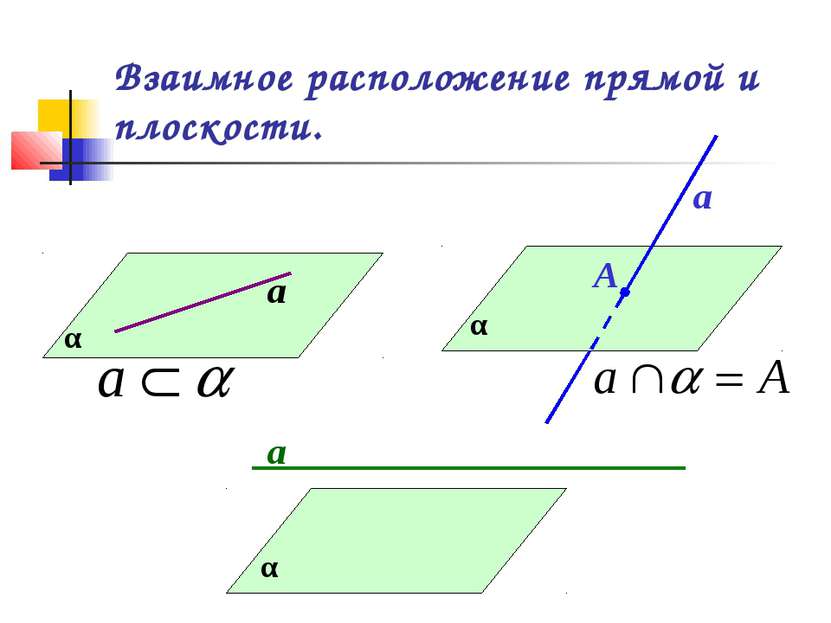
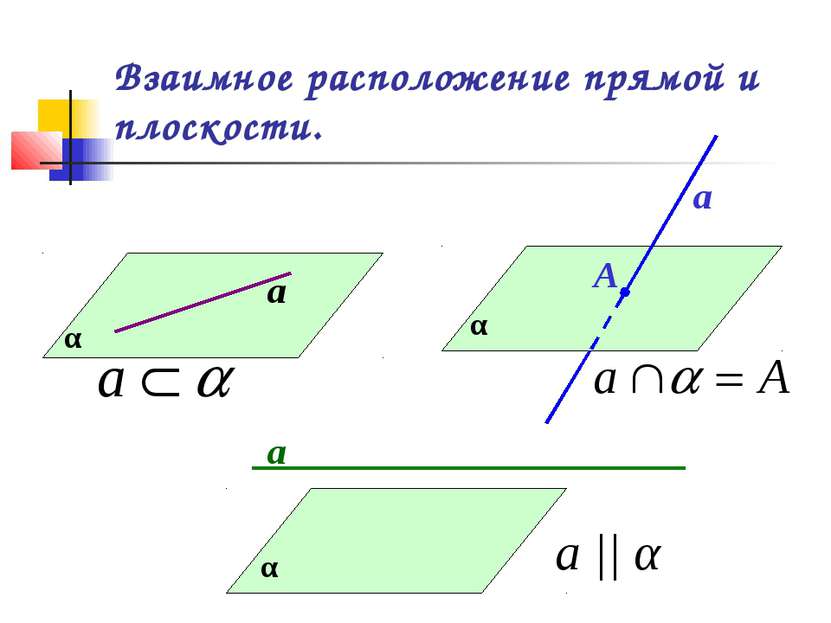
Взаимное расположение прямой и плоскости
Скачать эту презентациюПрезентация на тему Взаимное расположение прямой и плоскости
Скачать эту презентациюCлайд 1
 Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости. МОУ СОШ №256 г.Фокино. 2007 г.
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости. МОУ СОШ №256 г.Фокино. 2007 г.
Cлайд 3
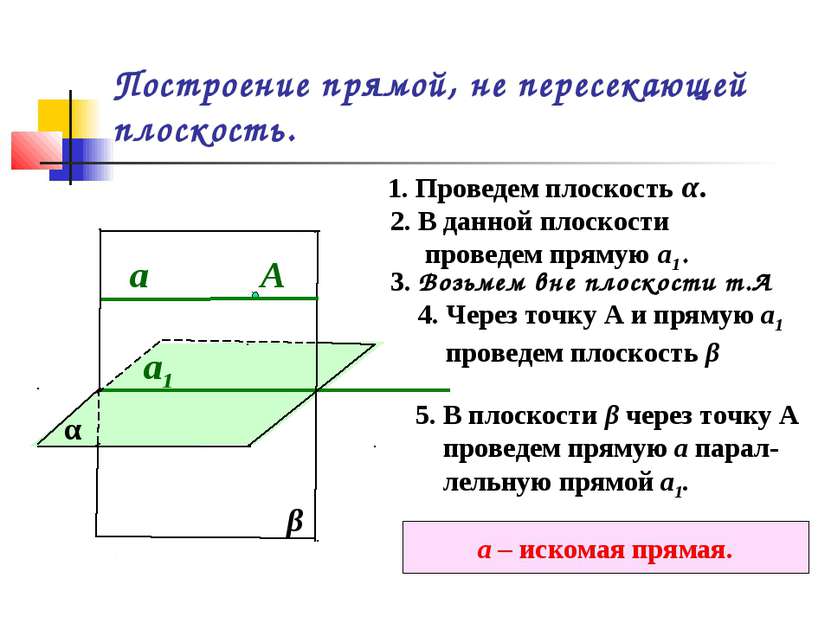
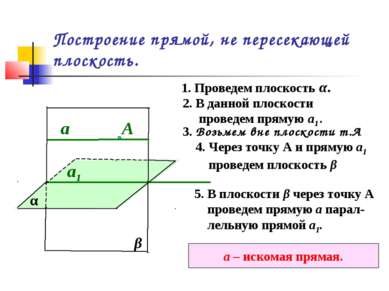 Построение прямой, не пересекающей плоскость. α 1. Проведем плоскость α. 2. В данной плоскости проведем прямую а1. а1 3. Возьмем вне плоскости т.А А 4. Через точку А и прямую а1 проведем плоскость β β 5. В плоскости β через точку А проведем прямую а парал- лельную прямой а1. а а – искомая прямая.
Построение прямой, не пересекающей плоскость. α 1. Проведем плоскость α. 2. В данной плоскости проведем прямую а1. а1 3. Возьмем вне плоскости т.А А 4. Через точку А и прямую а1 проведем плоскость β β 5. В плоскости β через точку А проведем прямую а парал- лельную прямой а1. а а – искомая прямая.
Cлайд 4
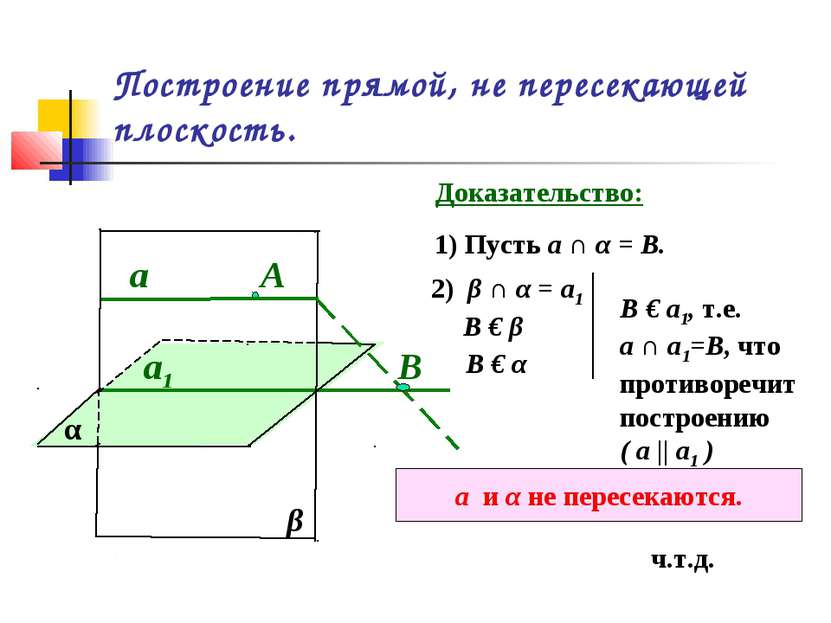
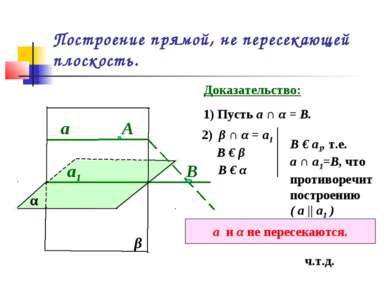 Построение прямой, не пересекающей плоскость. α а1 А β а Доказательство: 1) Пусть а ∩ α = B. В 2) β ∩ α = а1 В € β В € α В € а1, т.е. а ∩ а1=В, что противоречит построению ( а || а1 ) а и α не пересекаются. ч.т.д.
Построение прямой, не пересекающей плоскость. α а1 А β а Доказательство: 1) Пусть а ∩ α = B. В 2) β ∩ α = а1 В € β В € α В € а1, т.е. а ∩ а1=В, что противоречит построению ( а || а1 ) а и α не пересекаются. ч.т.д.
Cлайд 5
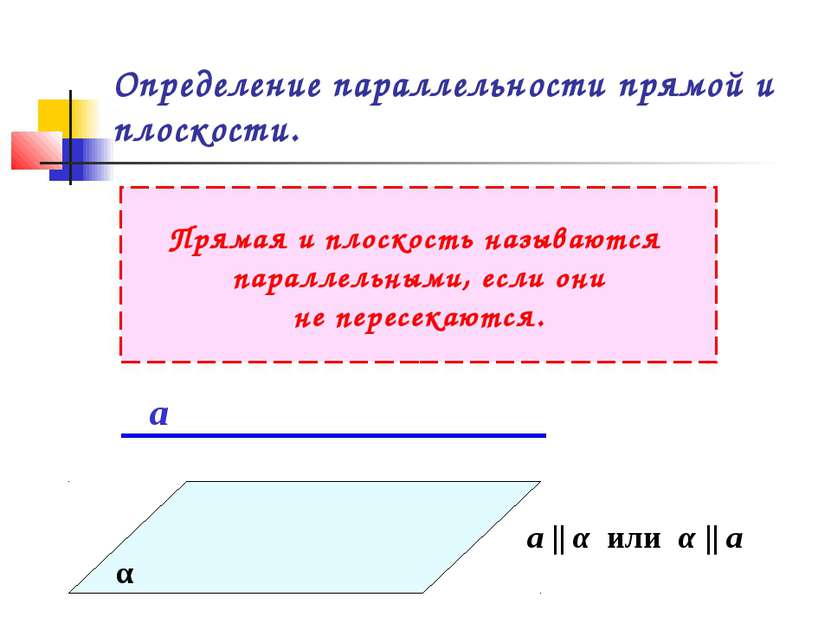
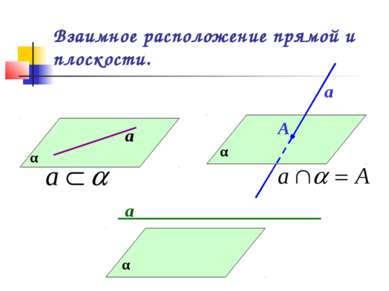
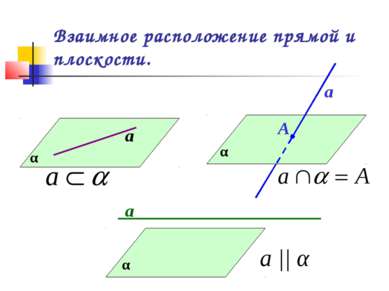
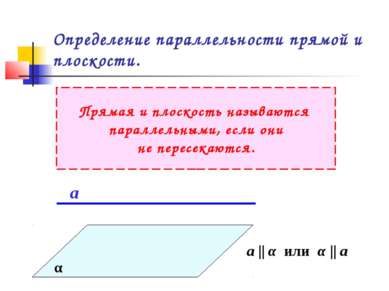 Определение параллельности прямой и плоскости. Прямая и плоскость называются параллельными, если они не пересекаются. α а а || α или α || а
Определение параллельности прямой и плоскости. Прямая и плоскость называются параллельными, если они не пересекаются. α а а || α или α || а
Cлайд 7
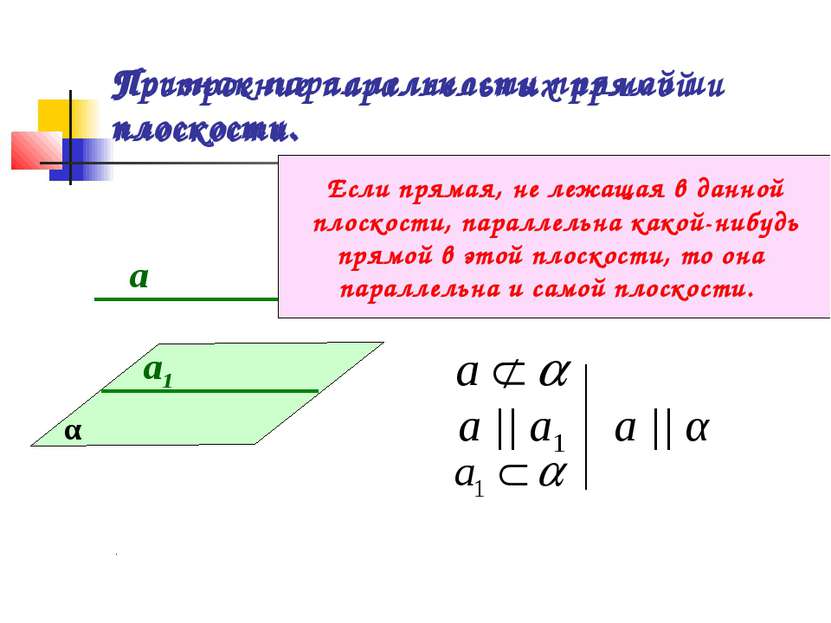
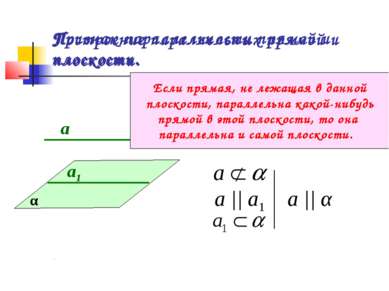 Построение параллельных прямой и плоскости. а1 а α а || а1 а || α Признак параллельности прямой и плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Построение параллельных прямой и плоскости. а1 а α а || а1 а || α Признак параллельности прямой и плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Cлайд 8
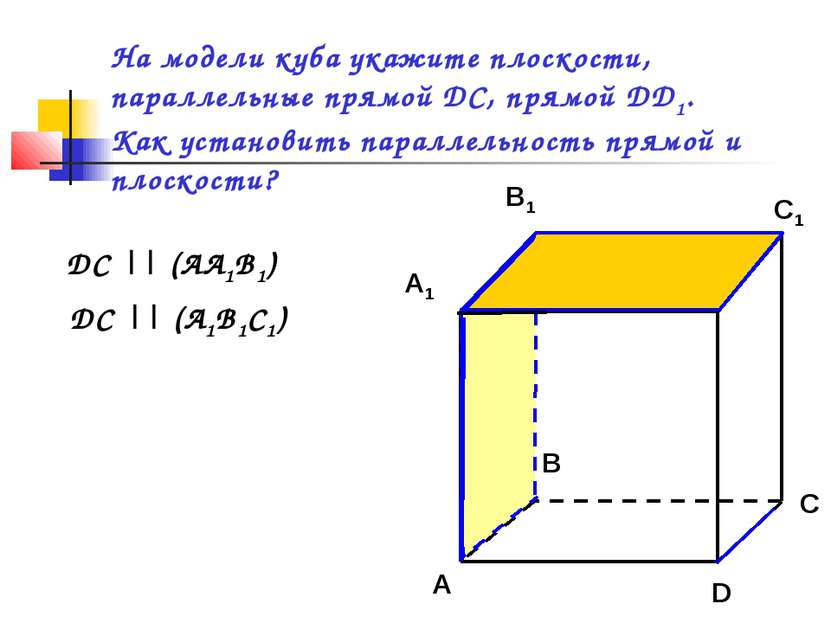
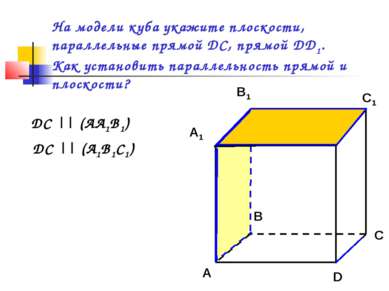 На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости? C1 C DC || (AA1B1) DC || (A1B1C1)
На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости? C1 C DC || (AA1B1) DC || (A1B1C1)
Cлайд 9
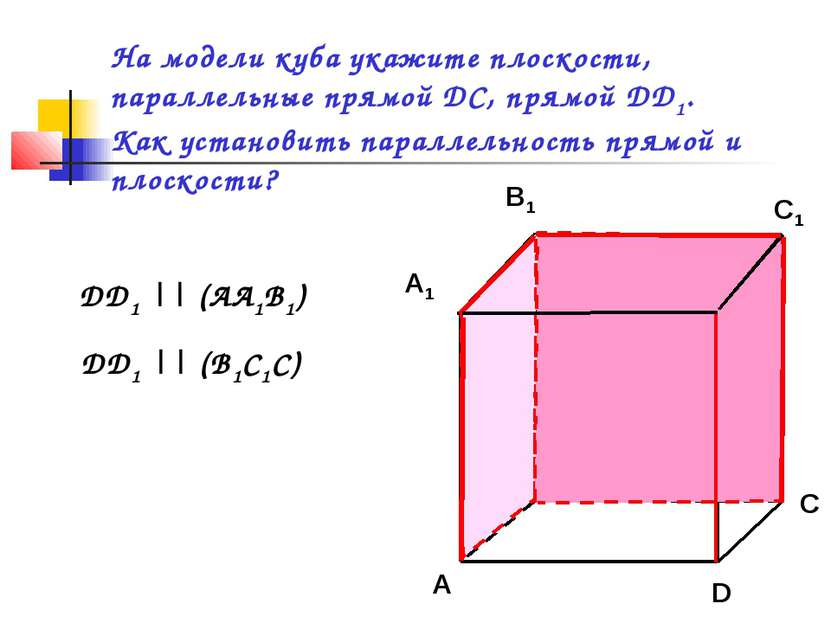
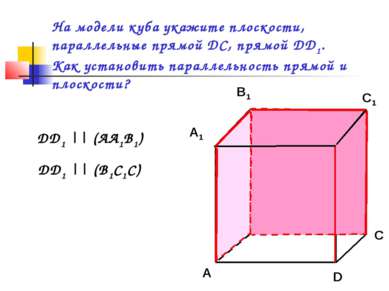 На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости? C1 C DD1 || (AA1B1) DD1 || (B1C1C)
На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости? C1 C DD1 || (AA1B1) DD1 || (B1C1C)
Cлайд 10
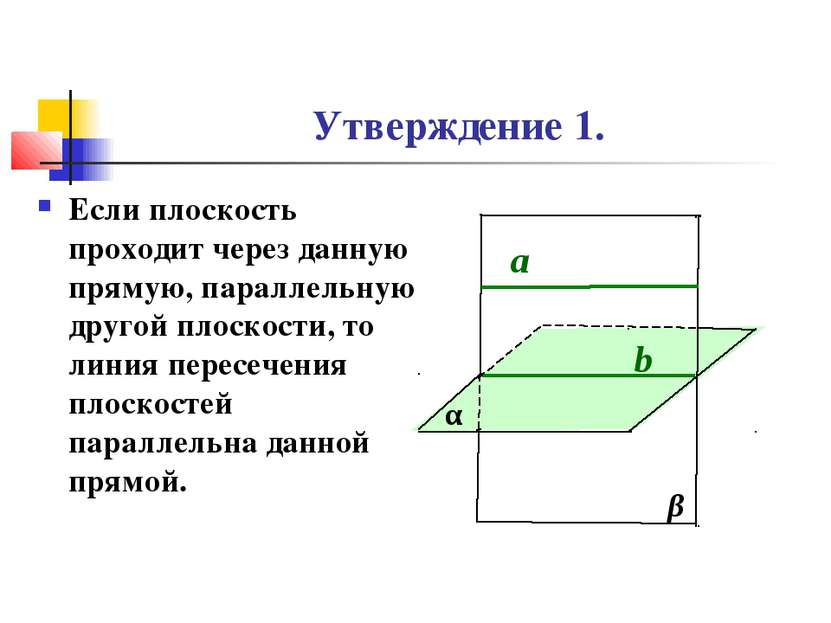
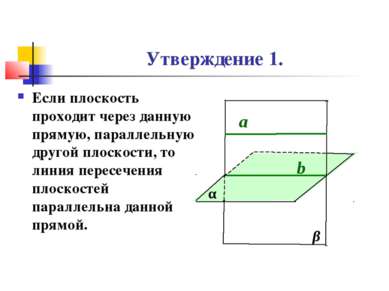 Утверждение 1. Если плоскость проходит через данную прямую, параллельную другой плоскости, то линия пересечения плоскостей параллельна данной прямой. α β а b
Утверждение 1. Если плоскость проходит через данную прямую, параллельную другой плоскости, то линия пересечения плоскостей параллельна данной прямой. α β а b
Cлайд 11
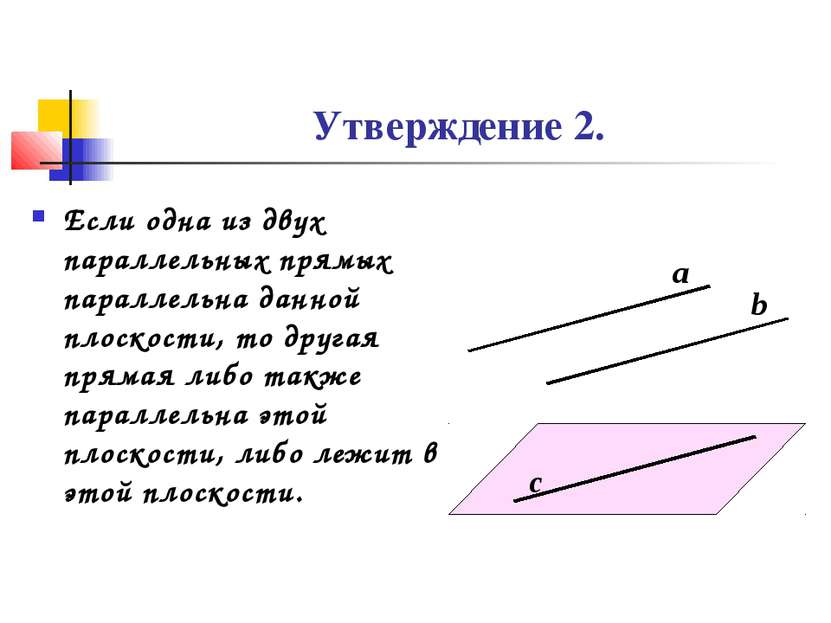
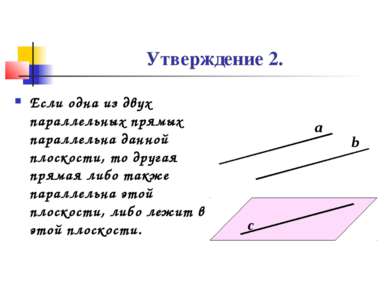 Утверждение 2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна этой плоскости, либо лежит в этой плоскости. а b с
Утверждение 2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна этой плоскости, либо лежит в этой плоскости. а b с