X
Код презентации скопируйте его
Наглядная геометрия 5-6 классов
Скачать эту презентацию
Презентация на тему Наглядная геометрия 5-6 классов
Скачать эту презентациюCлайд 1
Мосенкова Любовь Анатольевна Учитель математики МОУ сош №2 г.Вязьмы и школы «Интеллект»
Cлайд 2
Великий математик Принсгейм, сказал : «В математике живет всегда: художник, архитектор и даже поэт». Вот и мы с вами сегодня на уроке будем творить: рисовать и строить!
Cлайд 3
На листочках каждый ученик зарисовывает тот вид лица, который соответствует его настроению.
Cлайд 4
Цель: научить учащихся строить точки по заданным её координатам и определять координаты точки, отмеченной на координатной плоскости. Задачи: ознакомить учащихся с прямоугольной системой координат на плоскости; научить свободно ориентироваться на координатной плоскости; хорошо воспринимать на слух координаты; четко и аккуратно выполнять геометрические построения; развивать творческие способности; активизировать внимание учащихся с помощью применения мультимедийных средств; воспитывать интерес к предмету и ответственность за общий результат.
Cлайд 5
Координатная прямая или координатная ось (ось x) - - прямая на которой выбраны: начальная точка О (начало отсчета), масштаб (единичный отрезок, т.е отрезок, длина которого считается равной 1) положительное направление. 0 х 1
Cлайд 6
Сколько точек соответствует каждому числу на координатной прямой?
Cлайд 7
Чтобы правильно занять свое место, в кинотеатре нужно знать две координаты – ряд и место
Cлайд 8
Места в зрительном зале задают двумя числами: первым числом обозначают номер ряда , а вторым – номер кресла в этом ряду. Например, ряд 4 место 8 задаётся так-(4;8)
Cлайд 9
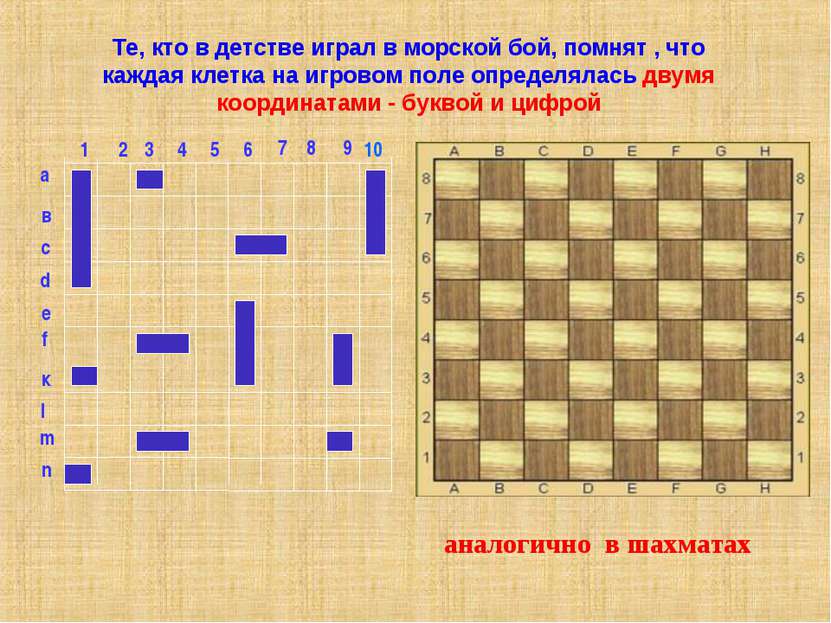
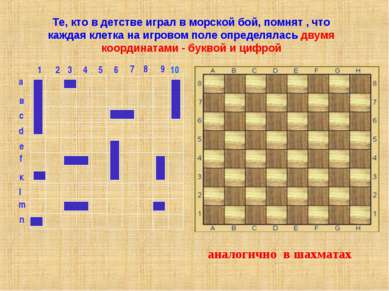Те, кто в детстве играл в морской бой, помнят , что каждая клетка на игровом поле определялась двумя координатами - буквой и цифрой а в с е f к l m n d 1 2 3 4 5 6 8 7 9 10 аналогично в шахматах
Cлайд 10
Система географических координат широта – параллели, долгота -меридианы
Cлайд 11
С помощью координатной сетки летчики, моряки определяют местоположение объектов;
Cлайд 12
Гиппарх Птолемей Рене Декарт
Cлайд 13
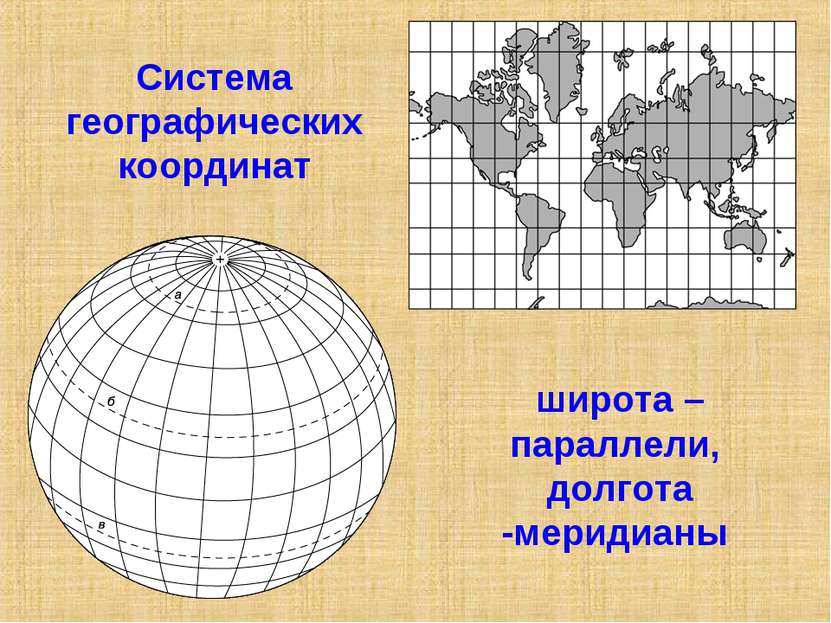
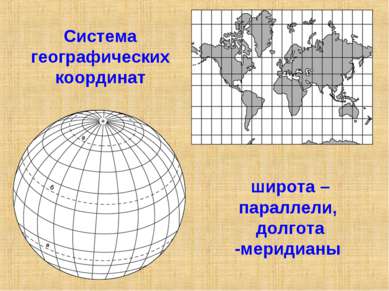
Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Cлайд 14
Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался долготой и широтой в качестве географических координат.
Cлайд 15
Рене Декарт (1596-1650) французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Автор координатной плоскости, поэтому ее часто называют декартовой системой координат.
Cлайд 16
Ось абсцисс О с ь о р д и н а т 0 Начало отсчета
Cлайд 17
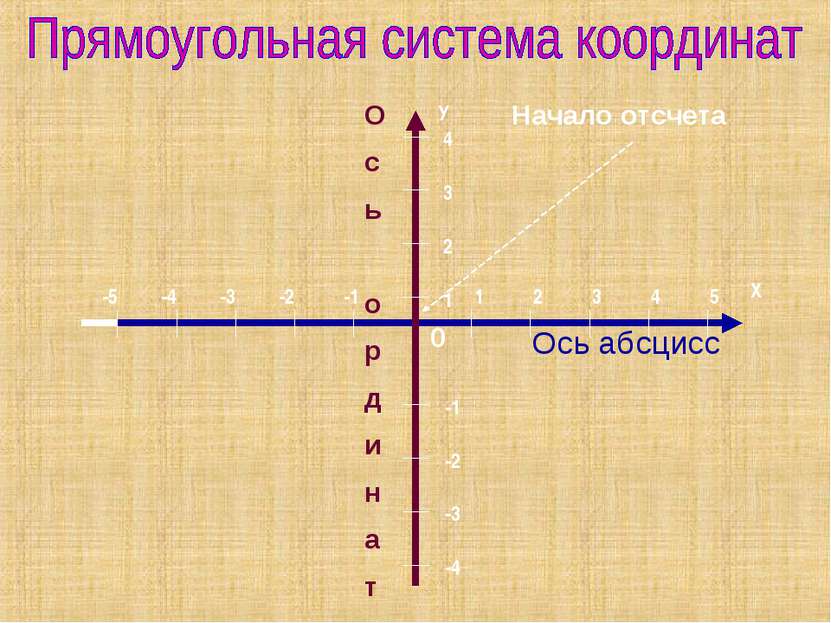
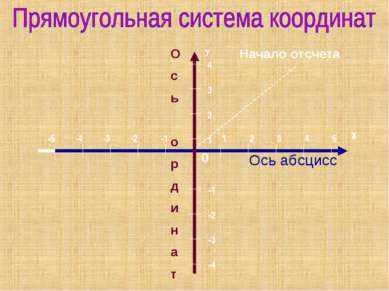
Плоскость, на которой выбрана прямоугольная система координат, называется Две перпендикулярные прямые c выбранным на них направлением единичным отрезком образуют прямоугольную систему координат. координатной плоскостью.
Cлайд 18
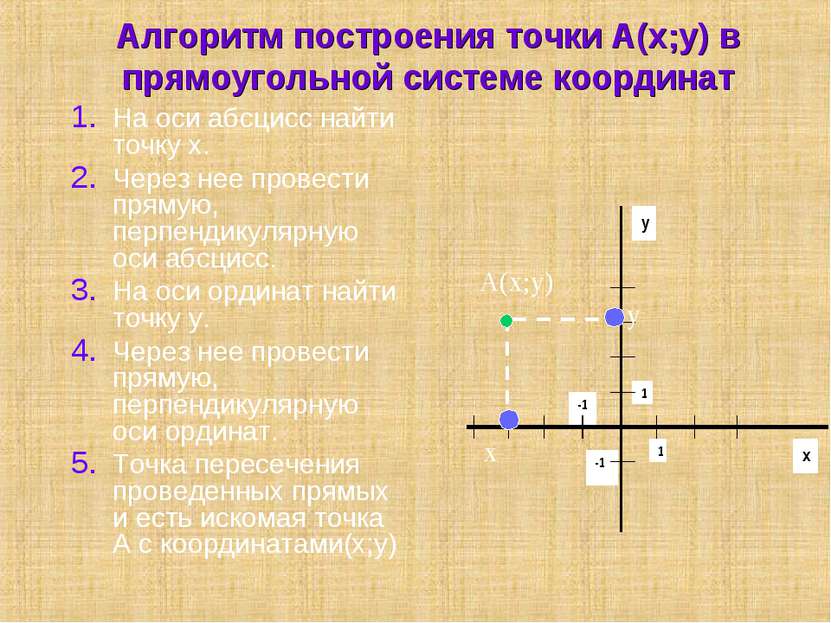
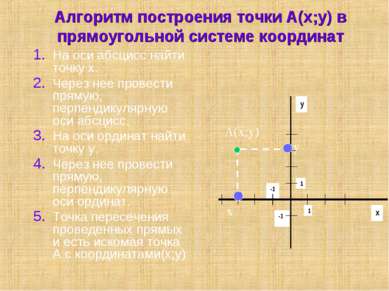Алгоритм построения точки А(х;у) в прямоугольной системе координат На оси абсцисс найти точку х. Через нее провести прямую, перпендикулярную оси абсцисс. На оси ординат найти точку у. Через нее провести прямую, перпендикулярную оси ординат. Точка пересечения проведенных прямых и есть искомая точка A с координатами(х;у) А(x;y) y x
Cлайд 19
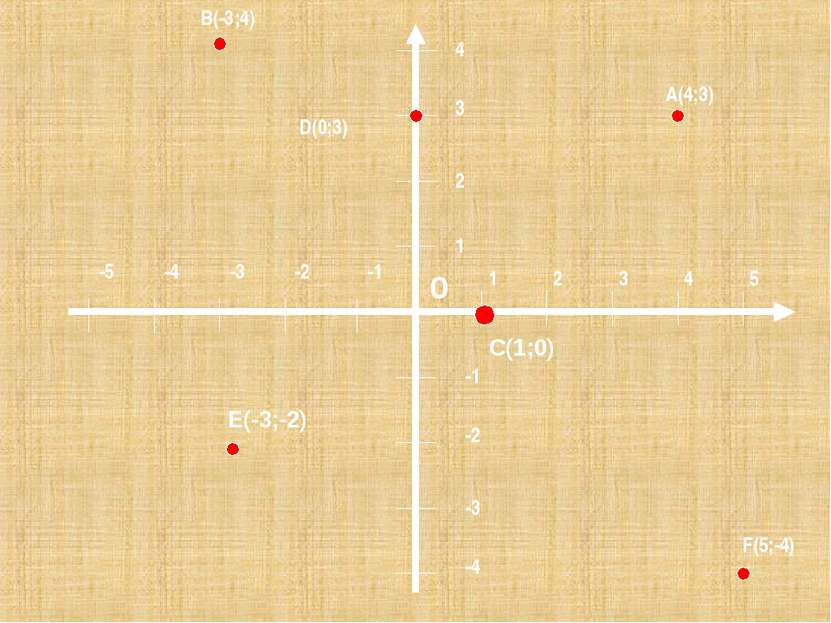
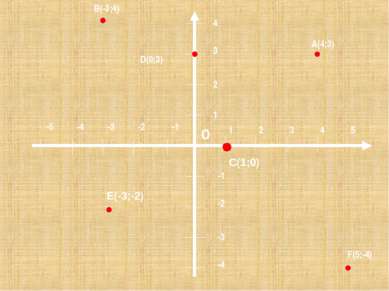
Начертите в тетради систему координат, взяв единичный отрезок длиной 1 см. Отметьте точки: А(4;3) В (-3;4) С(1;0) D(0;3) E(-3;-2) F(5;-4)
Cлайд 20
1 2 3 4 5 1 2 3 4 -1 -2 -3 -4 -1 -2 -3 -4 -5 B(-3;4) A(4;3) D(0;3) F(5;-4) C(1;0) E(-3;-2) 0
Cлайд 21
Отгадайте загадку: Я по России протекаю, Я всем известна, но, когда Ко мне прибавить букву с краю, Свое значенье я теряю И птицей становлюсь тогда.
Cлайд 22
Физкультминутка для глаз. 1. Посмотрите вправо и досчитайте до пяти;
Cлайд 23
2. Посмотрите влево (на счет раз, два, три, четыре, пять).
Cлайд 24
3. Посмотрите прямо: вверх и вниз.
Cлайд 25
4. Сделайте 5 круговых движений в одну сторону, потом в другую.
Cлайд 26
5. Теперь круговые движения в другую сторону.
Cлайд 27
6. Посмотрите вверх, вниз.
Cлайд 28
7. Посмотрите вниз и сделайте круговые движения глазами.
Cлайд 29
8. Посмотрите на кончик носа.
Cлайд 30
9. Посмотрите вдаль, поморгайте.
Cлайд 31
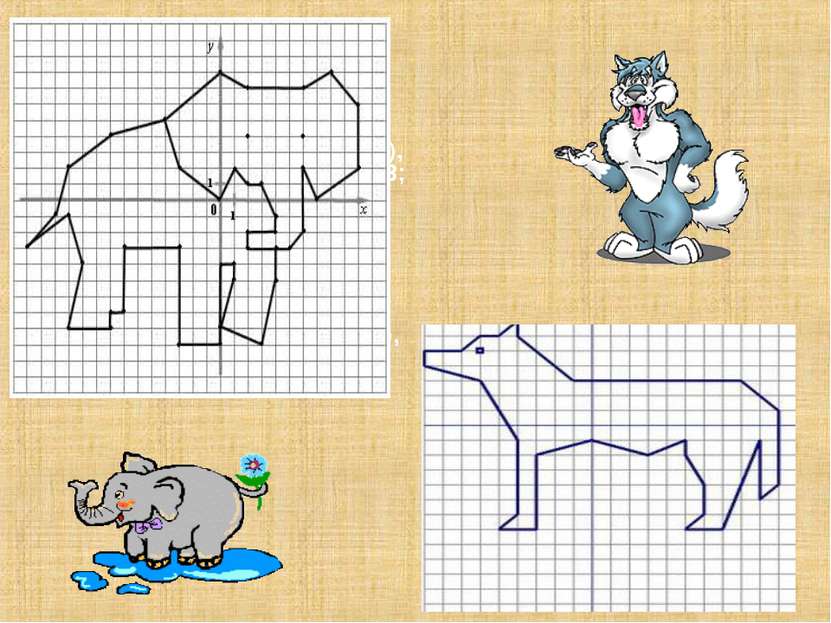
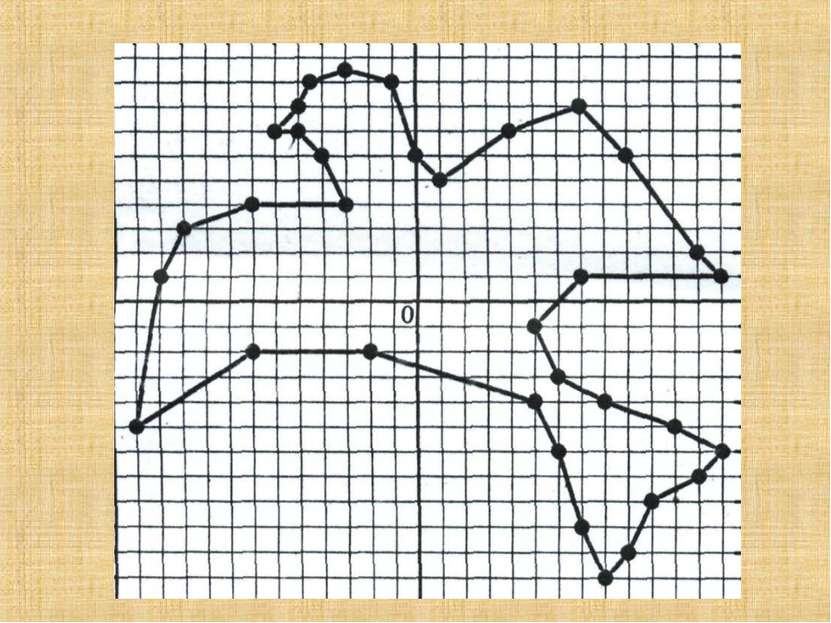
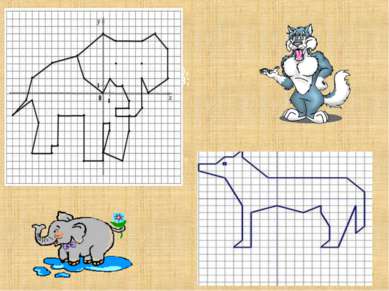Вариант 1 (2; - 3), (2; - 2), (4; - 2), (4; - 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5), (0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; - 2), (5; - 3), (2; - 3)(4; - 3), (4; - 5), (3; - 9), (0; - 8), (1; - 5), (1; - 4), (0; - 4), (0; - 9), (- 3; - 9), (- 3; - 3), (- 7; - 3), (- 7; - 7), (- 8; - 7), (- 8; - 8), (- 11; - 8), (- 10; - 4), (- 11; - 1), (- 14; - 3),(- 12; - 1), (- 11;2), (- 8;4), (- 4;5), (2; 4), (6; 4). Вариант2 (- 9; 5), (- 7; 5), (- 6; 6), (- 5; 6), (- 4; 7), (- 4; 6), (- 1; 3), (8; 3), (10; 1), (10; - 4), (9; - 5), (9; - 1), (7; - 7), (5; - 7), (6; - 6), (6; - 4), (5; - 2), (5; - 1), (3; - 2), (0; - 1), (- 3; - 2), (- 3; - 7), (- 5; - 7), (- 4; - 6), (- 4; - 1), (- 6; 3), (- 9; 4), (- 9; 5). Глаз: (- 6; 5)
Cлайд 32
Домашнее задание: Самостоятельно создать картинку животного и записать координаты.
Cлайд 33
Cлайд 34
Cлайд 35
Cлайд 36
Ну вот и закончилось наше познавательное путешествие. ВСЕМ СПАСИБО за урок!!!
Cлайд 37
На листе бумаги обведите руку и напишите на соответствующих пальцах свое отношение к геометрии: . на большом –интересное; 2. на указательном – полезное; 3. на среднем – затруднения; 4. на безымянном – пожелания; 5. на мизинце – общие впечатления о предмете. :
