X
Код презентации скопируйте его
Множество. Элемент множества
Скачать эту презентацию
Презентация на тему Множество. Элемент множества
Скачать эту презентациюCлайд 1
Множество. Элемент множества.
Cлайд 2
Cлайд 3
Множество: множество четных чисел; множество двузначных чисел; множество правильных дробей со знаменателем 5; множество диагоналей многоугольника; множество точек координатной плоскости; множество прямых, проходящих через данную точку.
Cлайд 4
Объекты или предметы, составляющие множество, называют элементами множества. Например: число 89 – элемент множества двузначных чисел.
Cлайд 5
Cлайд 6
Множества бывают конечные и бесконечные. Например: множество двузначных чисел – конечное множество (оно содержит 90 элементов), а множество четных чисел – бесконечное множество.
Cлайд 7
Cлайд 8
Пустое множество
Cлайд 9
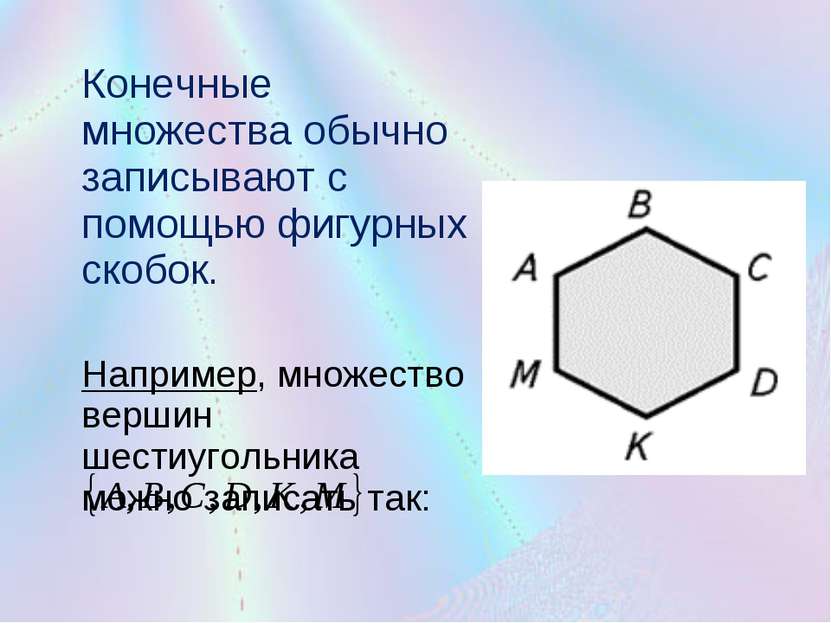
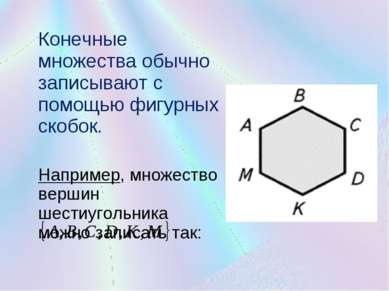Конечные множества обычно записывают с помощью фигурных скобок. Например, множество вершин шестиугольника можно записать так:
Cлайд 10
Множества принято обозначать большими буквами латинского алфавита. Например, можно записать так
Cлайд 11
Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой N (от латинского слова natural – «естественный», множество целых чисел – буквой Z (от немецкого слова zahl – «число», множество рациональных чисел – буквой Q (от латинского слова quotient – «отношение»).
Cлайд 12
В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного множества) или громоздко (как для конечного множества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т.е. свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.
Cлайд 13
множество всех натуральных чисел от 1 до 14 включительно; множество всех натуральных чисел, меньших 15; множество значений х, где и Тот факт, что множество А состоит из элементов х, удовлетворяющих этим условиям, будем записывать так:
