X
Код презентации скопируйте его
Разложение вектора по двум неколлинеарным векторам (9 класс)
Скачать эту презентацию
Презентация на тему Разложение вектора по двум неколлинеарным векторам (9 класс)
Скачать эту презентациюCлайд 1
Разложение вектора по двум неколлинеарным векторам Геометрия 9 класс
Cлайд 2
Лемма: Если векторы а и b коллинеарны и а 0, то существует такое число k, что b = ka Доказательство:
Cлайд 3
Cлайд 4
Cлайд 5
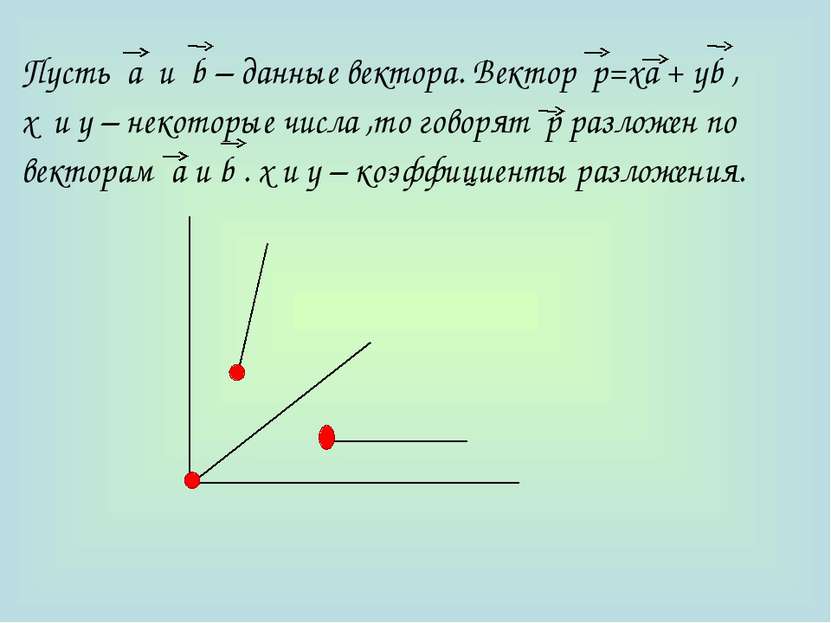
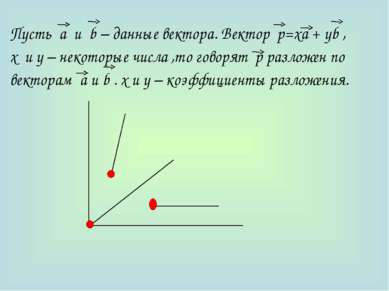
Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
Cлайд 6
Доказательство: Пусть а и b - неколлинеарные векторы. Докажем , что любой вектор р можно разложить по векторам а и b. Пусть р коллинеарен b . Тогда р = уb , где у – некоторое число р = 0· а + у·b ,т.е. р разложен по векторам а и b .
Cлайд 7
Координаты вектора А В
Cлайд 8
x y 0 i j
Cлайд 9
x y 0 i j
Cлайд 10
x y 0 i j
Cлайд 11
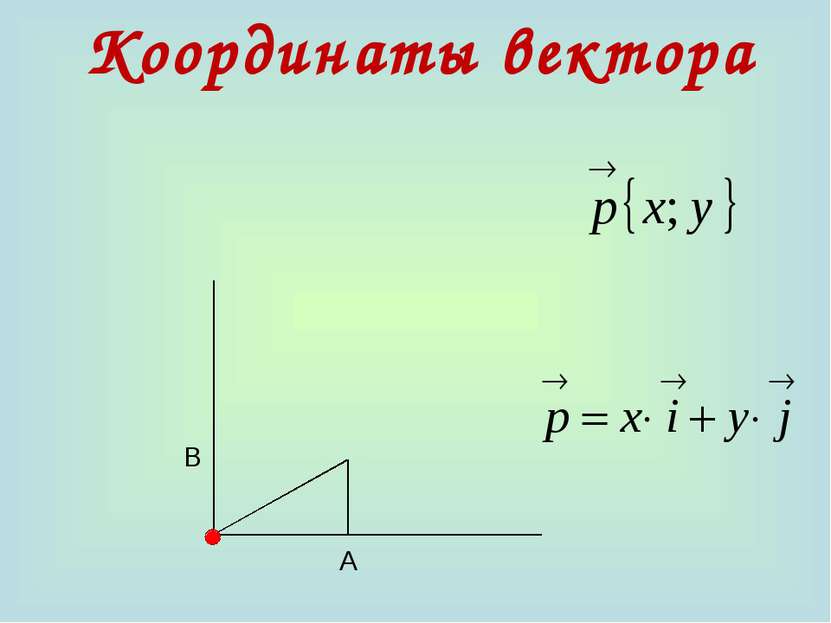
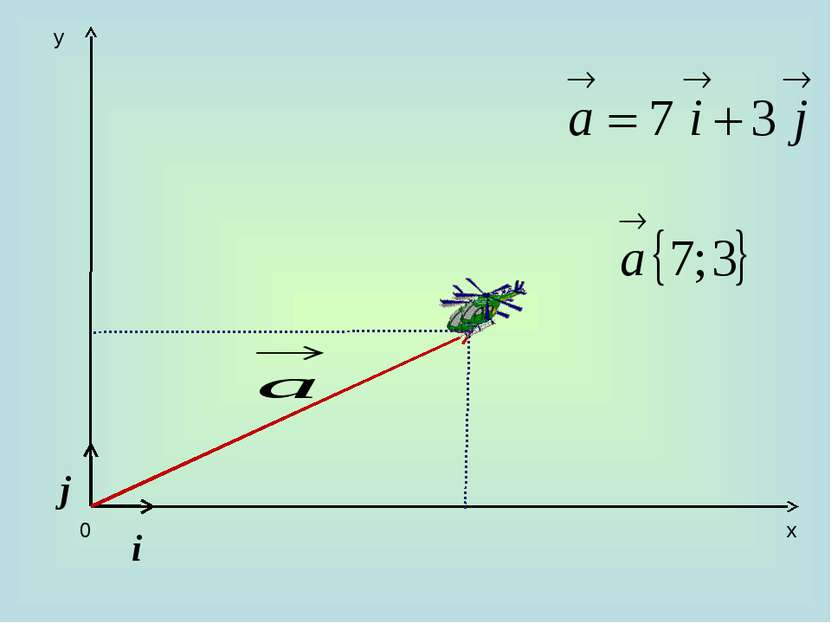
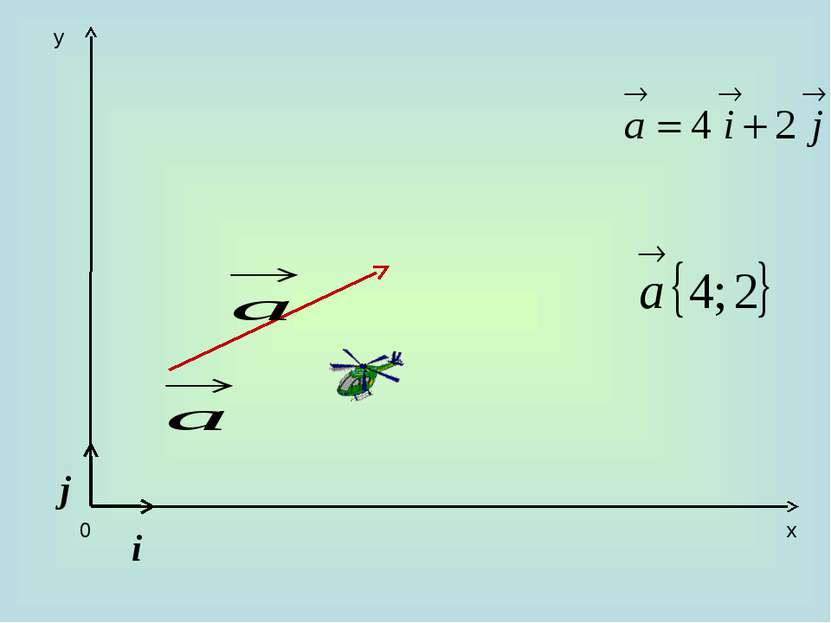
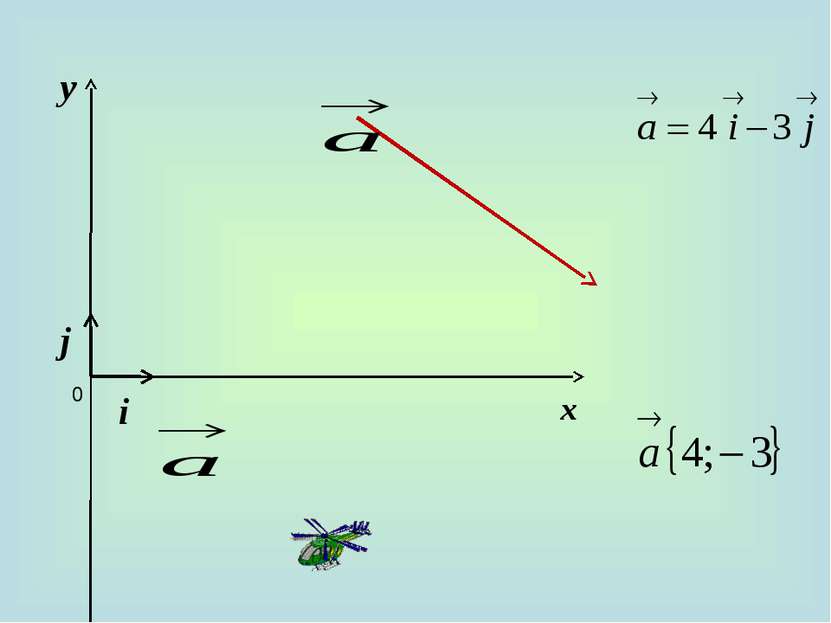
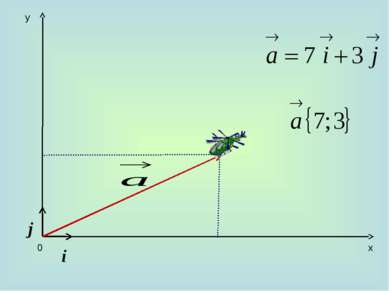
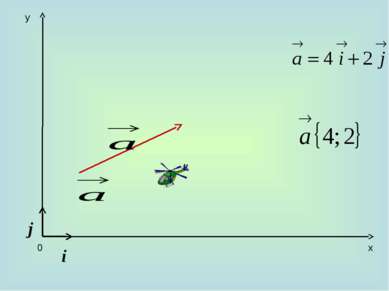
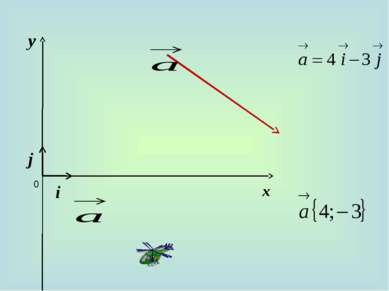
10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. а+b=(х1+х2)i + (у1+у2)j 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. а-b=(х1-х2)i + (у1-у2)j 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. ка =кхi +куj
