X
Код презентации скопируйте его
Системы двух линейных уравнений с двумя переменными
Скачать эту презентацию
Презентация на тему Системы двух линейных уравнений с двумя переменными
Скачать эту презентациюCлайд 1
Урок алгебры в 7А классе МОУ ОСОШ №1 Учитель: Чехонина О. Г.
Cлайд 2
образовательные: -повторить понятие системы линейных уравнений с двумя переменными, ее решения, графический метод, метод подстановки, метод алгебраического сложения; - отработать способы решения системы линейных уравнений, рассмотреть применение систем как модели реальных ситуаций; - закрепить навыки построения графиков линейных функций; - формировать навыки самостоятельной работы; развивающие: - развивать логическое мышление, математическую речь, вычислительные навыки; - развивать умение применять полученные знания к решению прикладных задач; -расширение кругозора; воспитывающие: - воспитание познавательного интереса к предмету; - воспитание у учащихся дисциплинированности на уроках; - воспитание аккуратности, внимательности, рационального использования времени при выполнении заданий.
Cлайд 3
(4;0),(0;3),(-3;-2),(-5;0),(3;-2),(-3;4) Декарт.
Cлайд 4
1.Найти числа, противоположные данным: 3; -58; 0; 5,74; -8,1; 2. Решите уравнения: а) -8х = -24 ; б) 50х = -5; в) -18х = 1; г)
Cлайд 5
Cлайд 6
Определение линейного уравнения с двумя переменными. Что является решением линейного уравнения с двумя переменными? В каком случае говорят, что уравнения образуют систему? Что значит решить систему? Что является решением системы? Какие методы решения мы изучили?
Cлайд 7
Cлайд 8
Cлайд 9
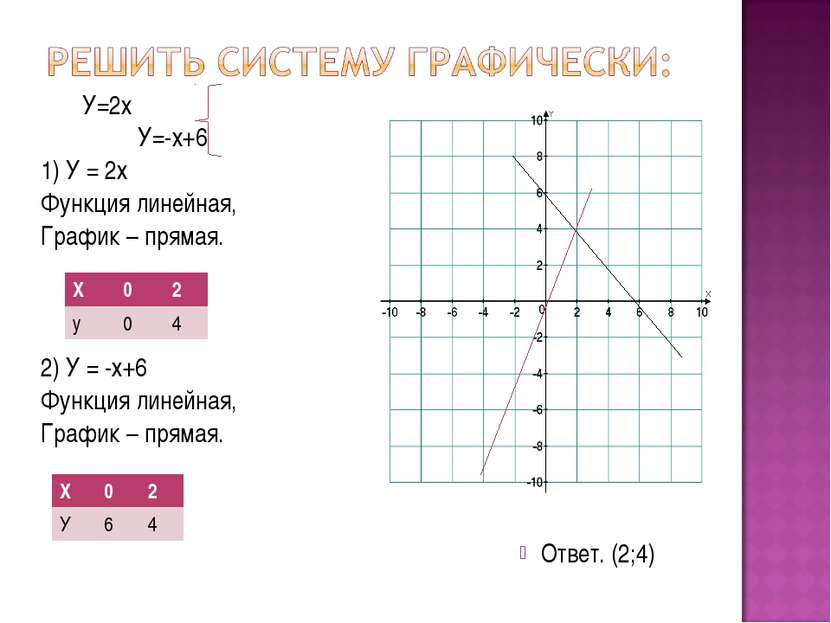
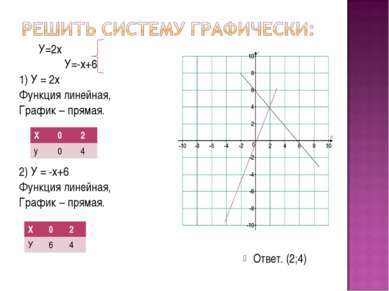У=2х У=-х+6 1) У = 2х Функция линейная, График – прямая. 2) У = -х+6 Функция линейная, График – прямая. Ответ. (2;4) Х 0 2 у 0 4 Х 0 2 У 6 4
Cлайд 10
Cлайд 11
х - у = 3, 2х +3у = 16; Решим второе уравнение: 6 + 2у + 3у = 16 5у = 16-6 5у = 10 у = 2 Х = 3+ у 2(3+у) + 3у = 16 у = 2 х = 3+у у = 2 х = 3+2 у = 2 х = 5 Ответ.(5;2)
Cлайд 12
Cлайд 13
Cлайд 14
Cлайд 15
«Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на алгебраический.»
Cлайд 16
Сумма двух чисел равна 7, а их разность 3.Найти эти числа. 1) х-у=7; х+у=3. 2) х+у=7; ху=3. 3) х+у=7; х-у=3.
Cлайд 17
Разность двух чисел равна 12. Одно из них больше другого в 4 раза. х – у = 12; х = 4у. В классе 36 учеников. Девочек на 3 меньше, чем мальчиков. х + у = 36; х – у = 3.
Cлайд 18
Из книги «Старинные задачи по элементарной математике» В.Д. Чистякова задача из китайского трактата «Девять отделов искусства счета», составленного в глубокой древности, которая звучит так: «5 волов и 2 барана стоят 11 таэлей, а 2 вола и 8 баранов стоят 8 таэлей. Сколько стоят отдельно вол и баран?»
Cлайд 19
Из «Курса алгебры» известного русского математика А.Н. Страннолюбского (1868г.), который был домашним учителем Софьи Ковалевской: «Некто на вопрос о возрасте двух его сыновей отвечал: «Первый мой сын втрое старше второго, а обоим им вместе столько лет, сколько было мне 29 лет тому назад; мне теперь 45 лет». Найдите возраст сыновей.
Cлайд 20
Задача в стихах: По тропинке вдоль кустов Шло одиннадцать хвостов. Насчитать я также смог, Что шагало тридцать ног. Это вместе шли куда-то Индюки и жеребята. А теперь вопрос таков: Сколько было индюков? Спросим также у ребят: Сколько было жеребят? Ты сумел найти ответ?
Cлайд 21
Декарт.
Cлайд 22
Дом.задание Творческое: составить задачу.
