X
Код презентации скопируйте его
Простые числа
Скачать эту презентацию
Презентация на тему Простые числа
Скачать эту презентациюCлайд 1
выполнила: ученица 7-го класса Третьякова Люда
Cлайд 2
План работы: Определения простого числа Почему я выбрала эту тему Цели и задачи работы Теоретическая часть: исторические сведения; свойства простых чисел Практическая часть: нахождение простых чисел, путем освоения метода «Решето Эратосфена»; составление таблицы Заключение Использованная литература
Cлайд 3
Определение простого числа. Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число. Например: 3 – простое число. Оно нацело делится на 1 и на само себя, т.е. на 3. Если число имеет более двух делителей, то называется составным.
Cлайд 4
Почему я выбрала эту тему? В 6 классе мы проходили тему «Простые и составные числа», и меня настолько заинтересовала это тема, что я написала в прошлом году краткую исследовательскую работу на тему «Простые числа». В этом году продолжила свое исследование.
Cлайд 5
Предметом изучения является простые числа Целью данной работы является исследование некоторых свойств и нахождение простых чисел через освоение метода «Решето Эратосфена».
Cлайд 6
Для достижения этой цели перед собой поставила следующие задачи: 1. собрать и изучить материал. 2. открыть какие-либо закономерности и свойства в ряду чисел. 3. найти простые числа больше числа 997 методом «Решето Эратосфена».
Cлайд 7
I. Теоретическая часть Изучить историю и свойства простых чисел
Cлайд 8
Из истории простых чисел Греческий математик Эратосфен, живший более чем за 2000 лет до н.э., составил первую таблицу простых чисел, которая получила название «Решето Эратосфена». А почему решето? Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето.
Cлайд 9
Первый способ нахождения простых чисел Эратосфен записывал на дощечке, покрытым воском, и последовательно прокалывал составные числа. Таким образом, на доске нетронутыми остались лишь простые числа, а составные числа исчезали, как бы просеивались. Оставив нетронутым число 2, он далее прокалывал числа 4,6,8…, т.е. все четные числа, кратные двум. Следующее простое число 3, а все числа, кратные трем, уже составные, поэтому прокалывались все числа через два в третье. Оставив число 5 как простое, прокалываются все числа, кратные 5, т.е. каждое пятое число, и т.д.
Cлайд 10
Простыми числами занимался и древнегреческий математик Евклид (IIIв. до н.э.). В своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть ещё большее простое число.
Cлайд 11
Отсюда следует гипотеза мы можем найти простое число больше 997. Но предел простого числа не сумеем найти, т.к. они бесконечны
Cлайд 12
Свойства простых чисел Два простых числа, которые отличаются на 2, как 5 и 7, 11 и 13, 17 и 19 и т.д. получили образное название «близнецы». Три числа, которые отличаются на 2, называются «тройняшками», 3, 5, 7. Мы эти числа можем посмотреть в учебнике математики 6 класса
Cлайд 13
Cлайд 14
168 мест первой тысячи натуральных чисел занимают простые числа. Из них 16 чисел – палиндромические – каждое равно обращённому Например: 11,101, 131, 151, 181, 191, 313, 353, и т.д. симметричные себе простые числа: 107 – 701, 113 – 311, 149 – 941 и т.д., простые числа могут разместиться в магическом квадрате 571 1051 181 211 601 991 1021 151 631 823 1093 643 673 853 1033 1063 613 883
Cлайд 15
Среди простых чисел особую роль играют простые числа Мерсенна – числа вида Мр=2р-1. М2=22-1=3 т.е. М2=3, М3=7, М5=31, М7=127 Любое четное число, больше 2, можно представить в виде суммы 2-х простых чисел. Например: 4=2+2, 6=3+3, 8=5+3, 10=3+7, 12=5+7, 14=7+7, 16=11+5, 18=7+11, 20=3+17 и т.д. Но это утверждение не доказано. Такую задачу называют проблемой Варинга
Cлайд 16
Любое нечетное число больше 5, можно представить в виде суммы трех простых чисел. Например: 7=2+3+2, 9=2+5+2, 11=5+3+3, 13=5+5+3, 15=7+5+3, 17=5+5+7, 19=5+7+7, 21=3+7+11, 23=5+7+11, 25=17+3+5 и т.д.
Cлайд 17
II. Практическая часть Нахождение простых чисел больше 997 методом «Решето Эратосфена» и составление таблицы
Cлайд 18
Нахождение 92 простых чисел больше 997 методом «Решето Эратосфена»
Cлайд 19
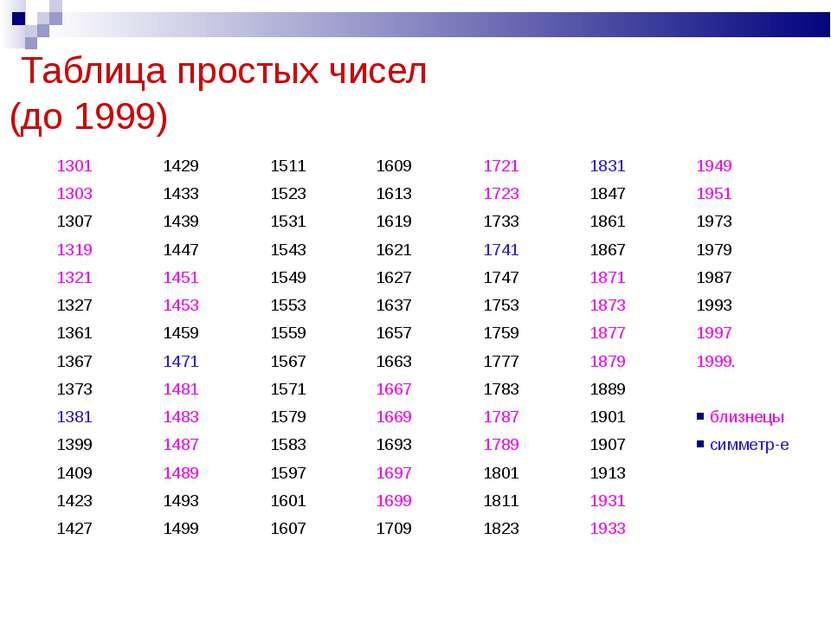
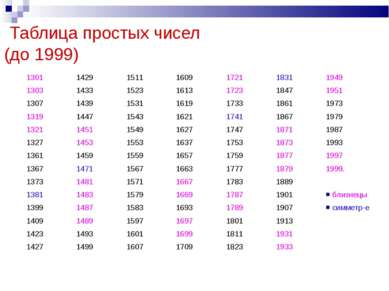Таблица простых чисел (до 1999) 1301 1429 1511 1609 1721 1831 1949 1303 1433 1523 1613 1723 1847 1951 1307 1439 1531 1619 1733 1861 1973 1319 1447 1543 1621 1741 1867 1979 1321 1451 1549 1627 1747 1871 1987 1327 1453 1553 1637 1753 1873 1993 1361 1459 1559 1657 1759 1877 1997 1367 1471 1567 1663 1777 1879 1999. 1373 1481 1571 1667 1783 1889 1381 1483 1579 1669 1787 1901 близнецы 1399 1487 1583 1693 1789 1907 симметр-е 1409 1489 1597 1697 1801 1913 1423 1493 1601 1699 1811 1931 1427 1499 1607 1709 1823 1933
Cлайд 20
Заключение: В своей работе «Простые числа», изучена история, свойства простых чисел. Отсюда сформулировала гипотезу, что указать самое большое простое число невозможно, т.к. они бесконечны. Эту теорему доказал древнегреческий математик Евклид III в. до н.э. В ходе работы были найдены 92 простые числа методом «Решето Эратосфена».
Cлайд 21
Использованная литература Учебник «Математика 6 класс», Н.Я.Виленкин, В.И. Жохова и др.изд. «Мнемозида», Москва 2007 Школьная энциклопедия «Математика. Том 11». Издательство «Аванта+»., М. 2003 Энциклопедия для детей «История Древнего мира». Издательство «Олимо-пресс Образования»., М 2003 Предметная неделя истории в школе. Составители: И.И. Варакина, С.В. Парецкова. Издательство «Корифей», Волгоград Шамаев Иван Иванович «Учись открывать новое». Издательство «Бичик»., Якутск: 1999г диск «Портфолио 3» Занятные стайки простых чисел
Cлайд 22
